2009年12月26日星期六.pku2165 计算几何

2009年12月26日星期六.pku2165 计算几何

2009年12月26日星期六.pku2165
计算几何
算法：将窗口投影到yz平面和xz平面，分别计算

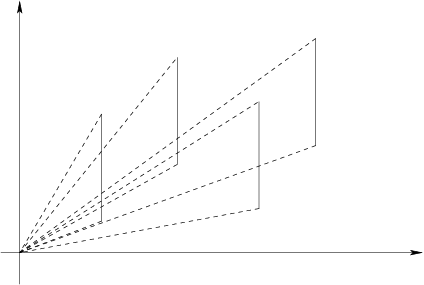
上图是投影到yz平面的情况，可以算出斜率的交区间，如果不存在则无解，然后随便从中选出一个斜率。
然后算出和第一个窗口的Y交点


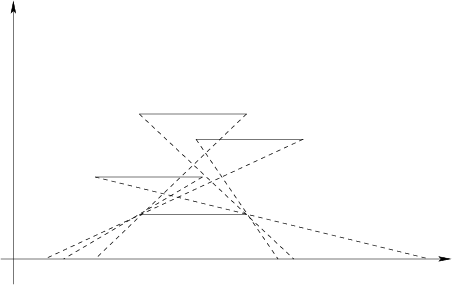
上图是投影到xz平面的情况，需要两两算出直线在x轴上的投影区间，然后随便选一个点作为出始点ansx。


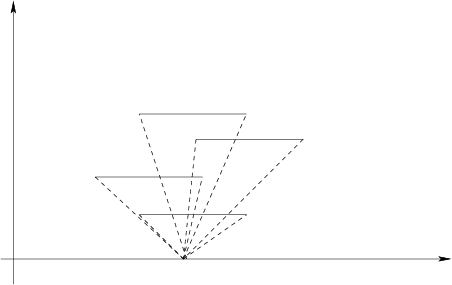
然后由这个点开始，算出斜率的交区间，进而求出和第一条窗的x交点

有了这两个点，就可以利用比例，求出和其他所有窗的交点了
最后，很恶心的是精度，需要特别注意判断无解的情况，一定要用
int dcmp ( double x) { return (x > eps) - (x < -eps);}
我在精度上卡了好几次，最后double eps = 1e-10; 时过的

  1  /*  
  2   * SOUR:pku2165
  3   * ALGO:computational geometry
  4   * DATE: 2009年 12月 26日 星期六 21:31:06 CST
  5   * COMM:4
  6   *  */
  7  #include < iostream >
  8  #include < cstdio >
  9  #include < cstdlib >
 10  #include < cstring >
 11  #include < algorithm >
 12  #include < cassert >
 13  #include < cmath >
 14  using   namespace  std;
 15  typedef  long   long  LL;
 16  const   int  maxint  =   0x7fffffff ;
 17  const   long   long  max64  =  0x7fffffffffffffffll;
 18  const   int  N  =   128 ;
 19  int  n;
 20  double  h,ansx,offset;
 21  struct  W {
 22       double  x1,y1;
 23       double  x2,y2,z;
 24  }w[N];
 25 
 26  double  eps  =  1e - 10 ;
 27  int  dcmp( double  x) {  return  (x  >  eps)  -  (x  <   - eps);}
 28 
 29  const   double  inf  =  1e30;
 30 
 31  void  ckmax( double   & a, double  b) {  if (dcmp(a  -  b)  <   0 ) a  =  b; }
 32  void  ckmin( double   & a, double  b) {  if (dcmp(a  -  b)  >   0 ) a  =  b; }
 33 
 34  bool  CalcY()
 35  {
 36       int  i;
 37       double  up   =  inf,down  =   - inf;
 38       for (i  =   0 ;i  <  n;i ++ ) {
 39          ckmax(down,w[i].y1  /  w[i].z);
 40          ckmin(up,w[i].y2  /  w[i].z);
 41      }
 42       if (dcmp(down  -  up)  >   0 ) {
 43           return   false ;
 44      }
 45       double  tmp  =  (up  +  down) /   2 ;
 46      h  =  tmp  *  w[ 0 ].z;
 47       // printf("CalcY succeded h = %.6f\n",h);
 48       return   true ;
 49  }
 50 
 51  struct  P
 52  {
 53       double  x1,x2;
 54  }interval[N * N];
 55  int  top;
 56 
 57  double  dist( double  a, double  b) {  return  sqrt(a  *  a  +  b  *  b); }
 58 
 59  bool  CalcX()
 60  {
 61       int  i ,j;
 62       double  z,x,len,L;
 63      top  =   0 ;
 64       for (i  =   0 ;i  <  n;i ++ ) {
 65           for (j  =  i  +   1 ;j  <  n;j ++ ) {
 66              z  =  w[j].z  -  w[i].z;
 67              x  =  w[j].x2  -  w[i].x1;
 68              len  =  dist(z,x);
 69              L  =  w[j].z  *  len  /  (w[j].z  -  w[i].z);
 70              x  =  x / len  *  L;
 71              interval[top].x1  =  w[j].x2  -  x;
 72 
 73              z  =  w[j].z  -  w[i].z;
 74              x  =  w[j].x1  -  w[i].x2;
 75              len  =  dist(z,x);
 76              L  =  w[j].z  *  len  /  (w[j].z  -  w[i].z);
 77              x  =  x / len  *  L;
 78              interval[top].x2  =  w[j].x1  -  x;
 79 
 80              top  ++ ;
 81          }
 82      }
 83       double  left  =   - inf,right  =  inf;
 84       for (i  =   0 ;i  <  top;i ++ ) {
 85           // printf("[%d] x1= %.6f,x2 = %.6f\n",i,interval[i].x1,interval[i].x2);
 86          ckmax(left,interval[i].x1);
 87          ckmin(right,interval[i].x2);
 88      }
 89       // printf("left = %.6f,right = %.6f\n",left,right);
 90       if (dcmp(left  -  right)  >   0 ) 
 91           return   false ;
 92       // if(left > right) 
 93           // return false;
 94 
 95      ansx  =  (left  +  right)  / 2 ;
 96      left  =   - inf,right  =  inf;
 97       for (i  =   0 ;i  <  n;i ++ ) {
 98          ckmax(left,(w[i].x1  -  ansx)  /  w[i].z);
 99          ckmin(right,(w[i].x2  -  ansx)  /  w[i].z);
100      }
101       // assert(left < right);
102       double  mid  =  (left  +  right) / 2 ;
103      offset  =  mid  *  w[ 0 ].z;
104       return   true ;
105  }
106 
107 
108  int  main()
109  {
110       int  i,j,k;
111      scanf( " %d " , & n);
112       for (i  =   0 ;i  <  n;i ++ ) {
113          scanf( " %lf%lf " , & w[i].x1, & w[i].y1);
114          scanf( " %lf%lf%lf " , & w[i].x2, & w[i].y2, & w[i].z);
115      }
116       if ( ! CalcY()) {
117          printf( " UNSOLVABLE\n " );
118           return   0 ;
119      }
120       if ( ! CalcX()) {
121          printf( " UNSOLVABLE\n " );
122           return   0 ;
123      }
124 
125      printf( " SOLUTION\n " );
126      printf( " %.6f\n " ,ansx);
127       for (i  =   0 ;i  <  n;i ++ ) {
128           double  x  =  w[i].z  *  offset  /  w[ 0 ].z  +  ansx;
129           double  y  =  w[i].z  *  h       /  w[ 0 ].z;
130           double  z  =  w[i].z;
131          printf( " %.6f %.6f %.6f\n " ,x,y,z);
132      }
133       return   0 ;
134  }
135 
136