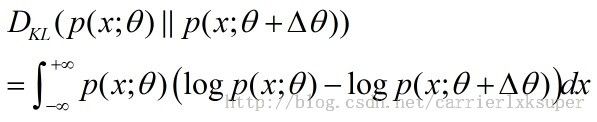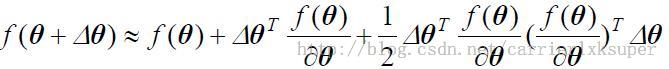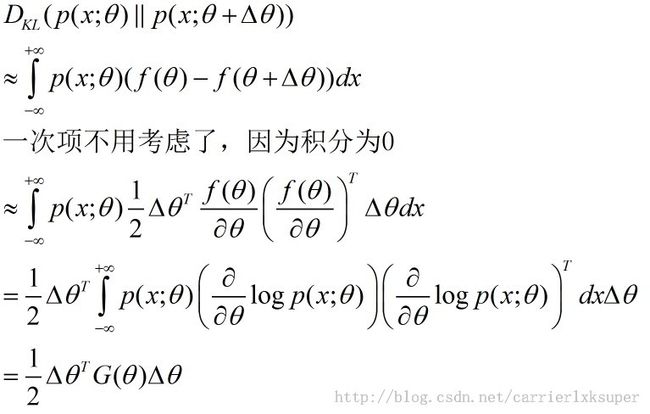信息几何,KL 散度以及流形
信息几何在wiki的定义是:information geometry is a branch of mathematics that applies the techniques of differential geometry to the field of probability theory. This is done by taking probability distributions for a statistical model as the points of a Riemannian manifold, forming a statistical manifold. The Fisher information metric provides the Riemannian metric.换句话说就是将信息学与几何学结合的学科,我们知道信息学的基础是概率与统计,而几何学的代表之一就是微分几何以及度量。结合的方法就是:将概率分布看做是黎曼流形中的某个点,从而形成了统计流形,在这个流形中,度量采用的是Fisher metric。
下面我们将引出为什么要研究信息几何,以及从空间转化的角度来理解信息几何。
考虑最简单的一个情况:梯度下降,gradient descent,公式就是:![]() ,其中theta是被估计的参数,而
,其中theta是被估计的参数,而![]() 指得是梯度。这个公式成立的一个重要的前提就是,自变量theta和因变量J(theta)都处于同一个空间,也就是欧氏空间中 ,于是他们采用的度量标准(metric)都是一样的。于是我们可以直接求出
指得是梯度。这个公式成立的一个重要的前提就是,自变量theta和因变量J(theta)都处于同一个空间,也就是欧氏空间中 ,于是他们采用的度量标准(metric)都是一样的。于是我们可以直接求出![]() 。但是在一些估计问题中,这个前提是不成立的,例如对于一组观测数值
。但是在一些估计问题中,这个前提是不成立的,例如对于一组观测数值![]() 和概率分布模型
和概率分布模型![]() ,theta是需要估计的参数。对于参数的变化(自变量),我们可以直接采用欧氏度量:
,theta是需要估计的参数。对于参数的变化(自变量),我们可以直接采用欧氏度量: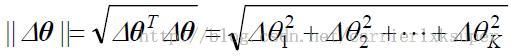 。但是由于自变量变化导致的因变量的变化也就是概率的变化无法用欧氏距离来进行度量。我们自然想到了度量概率分布的公式KL 散度。于是,对应的概率分布的变化:
。但是由于自变量变化导致的因变量的变化也就是概率的变化无法用欧氏距离来进行度量。我们自然想到了度量概率分布的公式KL 散度。于是,对应的概率分布的变化:![]() 的变化值就是:
的变化值就是: -------------------------------------1
-------------------------------------1
于是我们在进行梯度下降的时候,必须在p(x)的空间,使用的是KL距离,按照KL距离度量来使梯度下降或者上升达到最大,这样决定的梯度成为自然梯度。
那么有没有比较直观的方式来理解或者计算KL距离呢,因为这个距离与常见的欧氏距离差距太大了。这个时候我们就需要在黎曼几何下看待这个度量,而空间不再是欧氏空间而变成了统计流形上。我们做了一个空间转化。
如何理解流形呢?我自己发现有两个blog讲的很好:
http://blog.pluskid.org/?p=533
http://blog.sciencenet.cn/blog-722391-583413.html
好了,有了新的空间,有了新的度量标准了,我们到底如何简化一下KL的计算呢。
我们首先将上面的公式1写成;
然后我们令:![]() 以及
以及![]() ,再结合着函数展开,我们有:
,再结合着函数展开,我们有:
公式 2可以写成:
 ------------------------------3
------------------------------3
对于一次项,
于是公式3简化为:
G正好就是Fisher Matrix,这就对应到我们开头的关于度量标准采用fisher metric。
OK,所有的都清晰了,现在我们从空间转化的角度来理解这个信息几何。个人认为这种自然梯度计算的方法与欧氏空间下的不同坐标下的转换需要的雅克比算子是等价的,都需要一个转化子。信息几何就是在做这个工作,它通过空间转化,在新的空间下对于参数估计与计算会简单很多。
参考文献:
[1] http://en.wikipedia.org/wiki/Information_geometry
[2] 自然梯度.pdf