左堆(Leftist Heaps)
0)引论
为什么要提出左堆这么一个概念呢?有了二插堆还不够么。这是因为前面提到的数据结构在支持合并(merge)操作的时候是比较差的。比如对于一个二叉查找树来说,要把两个二叉查找树合并,那么可能需要把一个二叉树的结点一个一个的插入到另一个二叉树中,这个的时间消耗是一个很恐怖的事情。因此我们引入左堆。
1) 左堆的一些基本概念
零路径长(null path length)Npl(X):结点X到一个没有两个儿子的结点的最短路径的长度。这里我们定义没有两个儿子的结点的Npl(x) =0;Npl(NULL) = 0。
左堆和堆一样,也具有结构性质和堆序性质。左堆的结构性质是指:对于堆中的每一个结点X,它的左儿子的零路径长要不小于其右儿子的零路径长。
堆序信息与堆的一样,即:最小的结点应该是根节点,鉴于我们希望子树也是堆,那么每个子树的根节点也应该是最小的
这一性质必然会导致左堆是一个极其不平衡的树。
2) 左堆的基本操作
左堆的存在就是为了合并(merge),因此主要关注的就是怎样把两个左堆合并。
首先是左堆的一些声明
struct TreeNode;
typedef struct TreeNode *PriorityQueue;
struct TreeNode
{
ElementType Element;
PriorityQueue Left;
PriorityQueue Right;
int Npl;
}; 这个定义是很类似于树的定义的。因为堆也是一种树。
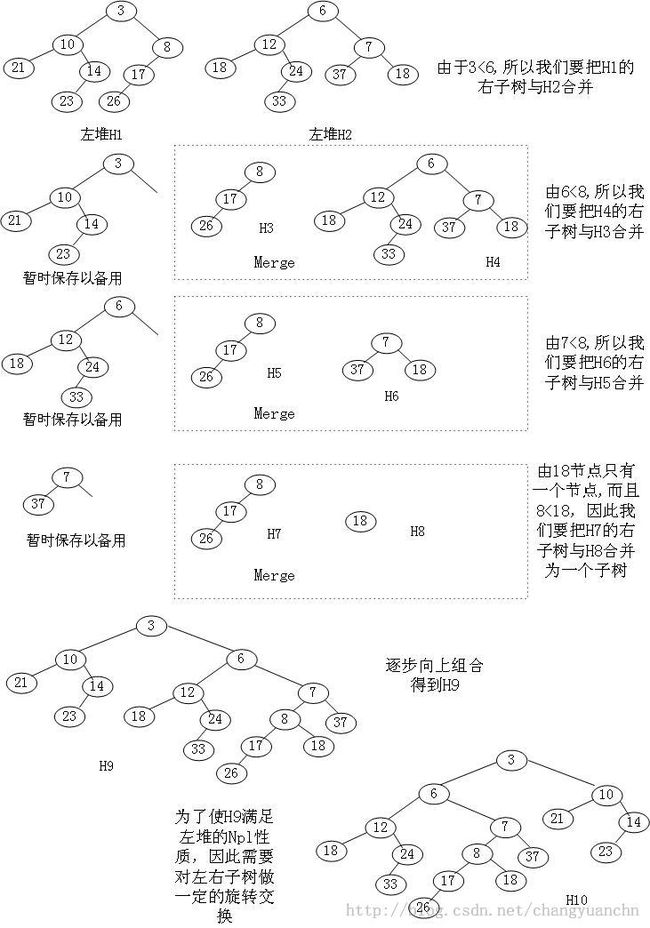
堆的合并:
由上图可见,堆的合并是一个递归的过程。
PriorityQueue Merge(PriorityQueue H1,PriorityQueue H2)
{
if(H1==NULL)
return H2;
if(H2==NULL)
return H1;
if(H1->Element<H2->Element)
return Merge1(H1,H2);
else
return Merge1(H2,H1);
}
static PriorityQueue Merge1(PriorityQueue H1,PriorityQueue H2)
{
if(H1->Left==NULl)
H1->Left = H2;
else
{
H1->Right = Merge(H1->Right,H2);
if(H1->Left->Npl<H1->Right->Npl)
swap(H1);
H1->Npl = H1->Right->Npl+1;
}
return H1;
}
插入可以看成是一个左堆和一个节点的合并:
PriorityQueue Insert(ElementType X,PriorityQueue H)
{
PriorityQueue SingleNode;
SingleNode = malloc(sizeof(struct TreeNode));
if(SingleNode==NULL)
Error("Out of Space!!!");
else
{
SingleNode->Element = X;
SingleNode->Left = SingleNode->Right = NULL;
SingleNode->Npl=0;
H = Merge(SingleNode,H);
}
return H;
}
合并两个左堆的时间复杂度为O(logN),因为这个相当于把右路径的长度相加。
删除最小:
本质:把根节点去掉,然后把剩下的左右子树合并
PriorityQueue DeleteMin(PriorityQueue H)
{
PriorityQueue LeftHeap, Rightheap;
if(IsEmpty(H))
{
Error("PriorityQueue is Empty");
return H;
}
else
{
LeftHeap = H->Left;
RightHeap = H->Right;
free(H);
return Merge(LeftHeap,RightHeap);
}
} 删除最小的时间复杂度也是O(logN),因为删除本质上是合并。
3) 总结
左堆的操作在本质上只有一个合并,切时间复杂度为O(logN)。插入和删除最小在本质上可以看成是合并。