拓扑排序(Topological Sort)
0)拓扑排序
拓扑排序是对有向无圈图的顶点的一种排序,这个排序的结果是如果存在一条vi到vj的路径,那么排序中vi在vj的前面。
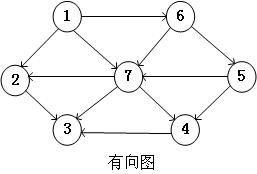
下图是一个有向无圈图的例子:
在这个有向无圈图中,1,6,5,7,4,2,3;1,6,5,7,2,4,3;这两组都是拓扑排序,我们可以看到这两种排序都满足拓扑排序的要求,比如说1-4的路径,可知1,7,4;1,6,5,4;1,6,7,4;1,6,5,7,4;这些路径的点都按照拓扑排序的要求排列。
1) 简单的拓扑排序算法
下面我们介绍一个简单的拓扑排序算法:
a)先找到一个没有输入边的点,输出这个点,然后去掉与这个点连接的所有边。
b)重复上面的步骤知道输出所有的点。
这里为了编程方便,我们要先定义一个叫做indegree的概念:
indegree: 顶点v包含的边(u,v)的个数。
注意是有向图的v包含的边(u,v)的个数。因此对于上图的点1,它的indegree=0,因为进入点1的边为0,点1的三条边全是指向外的。
所以通过引入indegree概念,上面的简单算法就可以用下面的方式表示
a) 查找indegree为0的点p
b) 对所有与p邻接的点的indegree = indegree -1;
c) 查找indegree为0的点(p除外),然后循环过程
下面是简单的拓扑排序算法的一段伪代码
void TopSort(Graph G)
{
int Num;
Vertex V,W;
for(Num=0;Num<NumVertex;Num++)
{
V = FindNewVertexOfDegreeZero();
if(V==NotVertex)
{
Error("Graph has a cycle!");
break;
}
Output[V] = Num;
for each W adjacent to V
Indegree[W]--;
}
}
上面的简单算法还是很简单的,也很好理解,那么为什么要改进上面的算法呢?这个主要是因为上面算法的时间复杂度为O(|V|^2)。
首先FindNewVertexOfDegreeZero()函数因为要找到indegree=0的点,所以需要遍历所有的点,因此时间复杂度为O(|V|)。而这个函数需要重复|V|次,因此上面的算法的时间复杂度为O(|V|^2)。因此我们需要做一些改进,来降低运行时间。
可以看到,这里可能能够进行改进的就是FindNewVertexOfDegreeZero()函数。当我们删除一个indegree=0的点后,只有与这个邻接的点的indegree才会减一,其他的点的indegree值不变,因此当我们需要在一次FindNewVertexOfDegreeZero时,不需要遍历所有的点,只需要遍历部分相关连的点就可以。
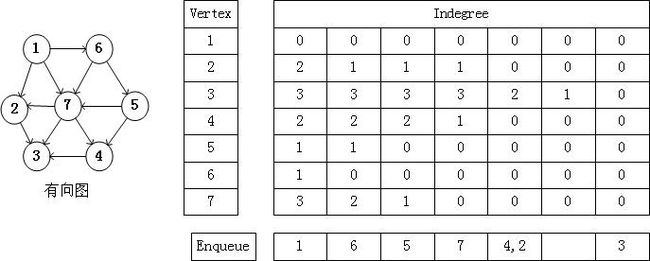
为了实现上面的思想,我们把indegree=0的点放到一个box中,因此FindNewVertexOfDegreeZero()函数只需要在这个box中寻找就好了。当一个点的indegree=0时,我们就把这个点输入到box中。
算法:
a) 把ndegree=0的点A放到一个Queue中;
b) 把点A出队,然后对所有的与A邻接的点的indegree减一;
c) 把新的ndegree=0的点入队;
d) 重复上面的步骤
伪代码实现:
void TopSort(Graph G)
{
Queue Q;
int Num=0;
Vertex V,W;
Q = CreateQueue(NumVertex);
MakeEmpty(Q);
while(!IsEmpty(Q))
{
V = Dequeue(Q);
TopNum[V] = ++Num;
for each W adjacent to V
if(--Indegree[W]==0)
Enqueue(W,Q);
}
if(Num!=NumVertex)
Error("Graph has a cycle!");
Free(Q);
}
这个方法相当于是以空间换时间,引入了一个Queue。