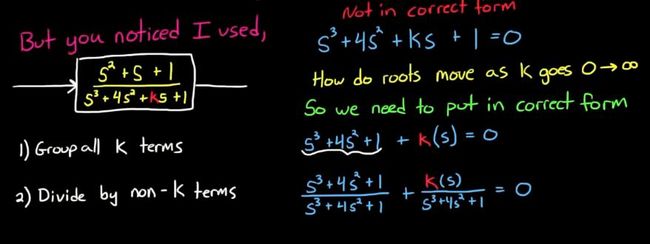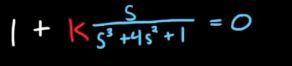root locus 徒手大致绘出根轨迹!一支笔,一张纸,足矣 自动控制原理
徒手绘制根轨迹
可以看出假设的系统传递函数如图中黄色公式部分
特征方程是(s^3+4*s^2+K*s+1) = 0;
绘制根轨迹的方法是
铺垫:
1) 先把所有和K有关的项合并成一大项K(s), (相当于提公因式K)
2) 接着把得到的式子除以不含K的项(如图中蓝色字体部分)
于是可以得到,这是变形后的特征方程
这个方程就变形为1+K * G(s) = 0 的形式了,很重要的铺垫
接着有几条规则需要注意 rule 1 和rule 2
Rule 1 看分子和分母谁的阶次高,把阶次高者的阶次标记为n,那么根轨迹有n条曲线
Rule 2 当K 从0增大到无穷大的时候,根的轨迹从传递函数的极点移动到传递函数的零点
上面的分析其实很精彩,极点和零点的定义分别是
利用这个定义,那么可以与K的变化很好的对应起来
K = 0的时候,P(s) = 0,此时是极点
K趋向于无穷大,而表达式为0,Q(s)必为0,是零点
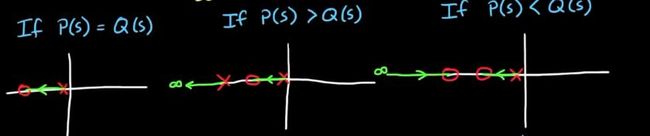
这就可以观察到,K越来越大的时候,是从极点趋向于零点的!
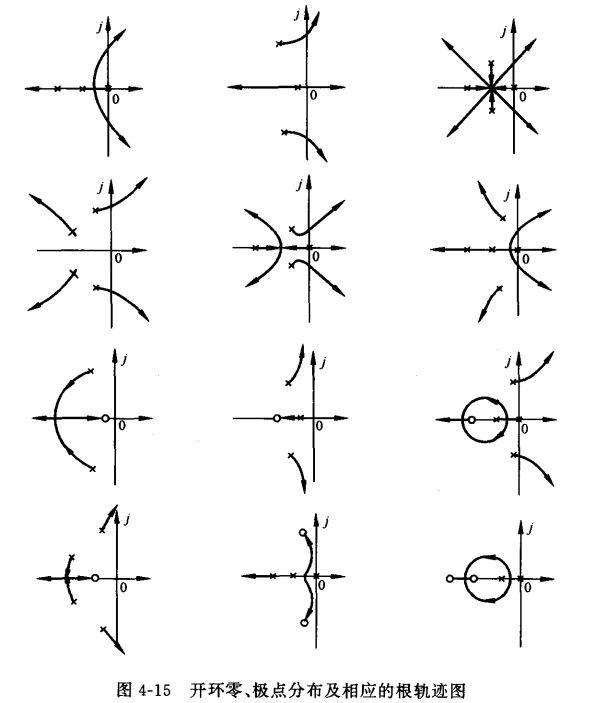
上图分别对应了极点数和零点数相等,极点数大于零点数,极点数小于零点数,三种情况的根轨迹大致分布图像
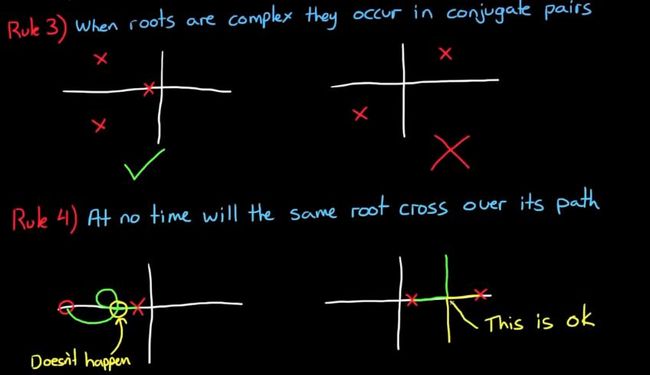
Rule 3 如果有的根是虚根,那么必定对称分布,不对称就错鸟。。。。
Rule 4 同一极点引出的根轨迹是不能重叠和自身发生交叉相遇的!(原谅我烂大街的翻译。。。)
简单的demo
三个极点一个零点:
1)3个极点比一个零点多,决定了系统的根轨迹有三条
2)有两条根轨迹将终止于无穷远处
3)图中ab极点根轨迹会对称分布
4)每个根轨迹不会交叉重叠
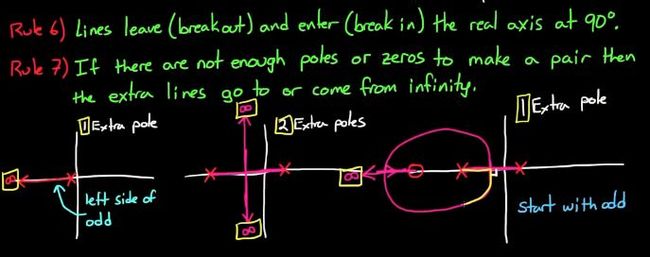
Rule 5 所有根轨迹上的点的右侧,极点和零点数目和为奇数
Rule 6 根轨迹会以和实轴夹角90度的方式离开实轴,直线延伸至无穷远处
Rule 7 如果这里没有足够的极点零点相互一一对应,对于多出的极点或者零点引出的根轨迹趋向于无穷远处
Rule 8 趋向于无穷远处根轨迹的渐近线(这里不是简简单单的一条规则能说清楚的,详细说明如下)
渐近线和实轴的夹角为theta = ( (2*q+1)/(n-m) ) * 180 此处q = n-m - 1,n是极点数,m是零点数
渐近线与实轴相交点 = ( (所有极点值的和)-(所有零点值的和) ) / (n - m)
如上图左下,只有一个极点的时候,theta = ( ( (2*(1-0-1)) +1 ) / (1-0) ) * 180 = 180
于是渐近线和实轴的夹角是 = 180°
右边两个极点的图,同理
当有三个极点的时候
n = 3 m = 0
q (max)= 3-0-1 = 2
于是q = 0 ,1, 2
对应的theta分别是60° 180° -60°
渐近线的交点是((-1-2-3)-0)/ (3-0) =- 2
这样就可以画出根轨迹啦!
4个极点的同理。。。。
Rule 9 如果这里有两条根轨迹是趋向于无穷远处的,那么所有根的和是一个常数
就是说图中如果-3处的极点左移,-1左移,-2右移,得到的三个新极点的和还是同一个常数
当K从0增大到负无穷大的过程中,这个时候得到的图像是和0从正无穷大的过程得到的图像关于虚轴对称的
求解分离点就是解这个方程即可
下图是各种根轨迹的demo
之前有个问题,故意没有强调,放在后面,现在说
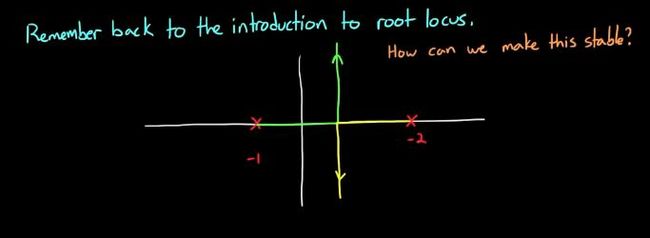
两个极点,有一个落到实轴正半轴上,导致根轨迹趋向于无穷的时候是落在正半轴这边的。系统不稳定
我用matlab 做了一个demo
怎么让系统变的稳定呢?
把趋向于无穷远的根轨迹落在正半轴部分的拉到负半轴去!
怎么拉?加零点!
这样系统就会趋于稳定了
beautiful !