Routh-Hurwitz Criterion 劳斯稳定判据
Routh-Hurwitz Criterion
为什么只要有一个极点在右半平面,那么系统就不会稳定?
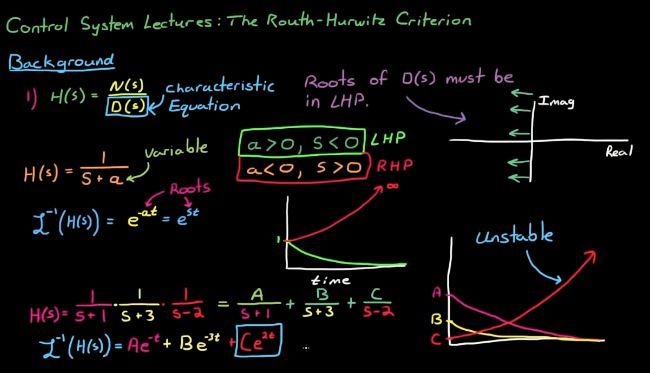
例如H(s) =( 1/(s+1) ) * ( 1/(s+3) ) * ( 1/(s-2) )
这里有个极点s = 2 在有半平面,通过laplace 反变换可以知道,当时间足够长的时候,AB都衰减的很厉害了,而C却还在增加,这时候系统是不会稳定的
于是紧紧抓住这个特性不放,就会引出劳斯稳定判据。
右半平面的极点可以通过特征方程来判定
只有当特征方程的所有系数都是同一个符号的时候,系统的根才会都落在左半平面
但凡有个特征方程系数有个符号不相同的出现,就会有根落在右半平面,这个时候系统就不会稳定
是不是特征方程所有的系数都相同那么所有的根就会落在左半平面呢?不一定!
下面这个例子就解出来0.5+_jsqrt(2.75)在右半平面,而所有的系数都是正数。
怎么检测这种不稳定的情况呢?答案是劳斯判据
假设特征方程系数矩阵是[ 1 2 3 10 8]
于是填入劳斯表
根据(BC-AD)/B 的法则,可以求出其他元素,从而得到第一列数据
如果第一列数据有一次符号变化,就说明右半平面有一个根,两次就有两个根在右半平面,依次类推
假设有个系统的开环传递函数的特征方程系数是[1 10 35 50 24+K]
运用劳斯稳定判据,系统要稳定,第一列数据都必须要同符号
进而可以求出满足稳定要求的K的范围
对劳斯表进行求解,解出,系统要稳定,K 必须小于126
几种特殊情况
special case 1:
当某行有0元素出现时,并且这个0后面还有非零元素时,这个时候计算劳斯判据时,将0替换成epsilon,然后继续算其他未知元素,最后令epsilon趋向于0,
可以得到第一列元素,如果发生符号的改变,那么 系统是不稳定的
special case 2:
当某一行整行都是0的时候
处理方法是把全0行的上一行列出P(s)表达式,例如下图中的P(s) = 6*s^2 + 12*s^0 = 0
对P(S)进行求导,于是把得到的系数填到原本是全零行的地方/
总结