第五章---排序

问题5.1 二分插入法

插入式排序法是一个极为简单的方法，但它的效率十分低，因为比较次数与n^2成正比，此处n是数据个数，而且还有大量移动数据的动作，请写一个程序，在这两点上改进，使得比较次数与nlogn成正比，而且移动数据的速度加快~

思路：为啥用二分查找不解释，memmov原型如下：void* memmov(void *dest, const void *src, size_t count);

#include <iostream>
#include <algorithm>
#include <iterator>

using namespace std;

#define YES 1
#define NO 0
#define SIZE sizeof(int) / sizeof(char)

void sort(int *input, int size)
{
	if (input == NULL || size <= 0)
		return;

	int current, pos;
	int low, high, mid;
	int x;

	for (current = 1; current < size; current++)
	{
		x = input[current];
		pos = -1;
		if (x < input[0])
			pos = 0;
		else if (x <= input[current - 1])
		{
			low = 0;
			high = current - 1;
			while (high - low > 1)
			{
				mid = (low + high) / 2;
				if (x >= input[mid])
					low = mid;
				else
					high = mid;
			}
			pos = low + 1;
		}
		if (pos >= 0)
		{
			memmove((void*)&input[pos + 1], (void*)&input[pos], SIZE * (current - pos));
			input[pos] = x;
		}
	}
}

void main()
{
	int array[] = {5, 2, 1, 4, 3, 7, 6};
	const int size = sizeof array / sizeof *array;

	sort(array, size);

	copy(array, array + size, ostream_iterator<int>(cout, " "));
}

问题5.2 SHELL

在传统的教科书中，Shell排列法都是直接饮用D.L.Shell当年原著中的办法，在要排序的数组中，先把间隔为n/2的元素排好，接着把间隔为n/4的元素排好，再排间隔为n/8 ... , 4, 2, 1的元素，最后就是一个依顺序排列完成的结果了。D.Knuth曾经在他的著作中证明，Shell方法要用与n^1.5成正比的比较次数（当然已经比插入排序要快了一些），不过最近Sedgewick等人却找出了更快的办法，他证明可以把Shell方法加快到只与n^4/3成正比的比较次数。请写一个程序，找出一组更快的间隔。

思路：哎，这道题很bug，不解释了。。。

问题5.3 快速排列法

可以找一本书，研究一下快速排列法的观点，写成程序。

快排写N次了，不写了~

问题5.4 保持等值的原来顺序

快速排序法有一个常被人批评的缺点，这就是相等的数据在排序完成后不会保持原来的顺序，不过，使用连接串行的技巧就可以轻易克服它，请写一个程序来完成这件工作。

思路：正是由于存在swap操作，快速排序法才会在相等的数据在排序完成后不会保持原来的顺序~

#include <iostream>
#include <algorithm>
#include <iterator>

using namespace std;

typedef struct node* Node;

struct node
{
	int data;
	Node next;
};

void list_quicksort(Node *, Node *);
Node insert(Node *, Node *, Node);
void join(Node *, Node *, Node, Node);
void printLink(Node head);

void sort(int *x, int n)
{
	if (x == NULL || n <= 0)
		return;

	Node first = NULL;
	Node last = NULL;
	Node p, q;
	int i;
	
	for (i = 0; i < n; i++)
	{
		p = (Node)malloc(sizeof(struct node));
		p->data = x[i];
		p->next = NULL;
		insert(&first, &last, p);
	}

	printLink(first);
	system("pause");

	list_quicksort(&first, &last);

	for (p = first, i = 0; i < n; i++)
	{
		x[i] = p->data;
		q = p;
		p = p->next;
		free(q);
	}
}

void printLink(Node head)
{
	while (head)
	{
		cout << head->data << " ";
		head = head->next;
	}
}

void list_quicksort(Node *first, Node *last)
{
	Node less_first = NULL;
	Node less_last = NULL;
	Node equal_first = NULL;
	Node equal_last = NULL;
	Node greater_first = NULL;
	Node greater_last = NULL;
	Node p;
	int pivot;

	pivot = (*first)->data;
	p = insert(&equal_first, &equal_last, *first);
	while (p != NULL)
	{
		if (p->data < pivot)
			p = insert(&less_first, &less_last, p);
		else if (p->data > pivot)
			p = insert(&greater_first, &greater_last, p);
		else
			p = insert(&equal_first, &equal_last, p);

		if (less_first != NULL)
			list_quicksort(&less_first, &less_last);
		if (greater_first != NULL)
			list_quicksort(&greater_first, &greater_last);
	}

	join(&less_first, &less_last, equal_first, equal_last);
	join(&less_first, &less_last, greater_first, greater_last);

	*first = less_first;
	*last = less_last;
}

Node insert(Node *first, Node *last, Node work)
{
	Node p;

	if (*first == NULL)
		*first = *last = work;
	else
	{
		(*last)->next = work;
		*last = work;
	}
	p = work->next;
	work->next = NULL;
	return p;
}

void join(Node *first, Node *last, Node head, Node tail)
{
	if (*first == NULL)
		*first = head, *last = tail;
	else if (head != NULL)
	{
		(*last)->next = head;
		*last = tail;
	}
}

void main()
{
	int array[] = {5, 3, 2, 1, 6, 7, 4};
	const int size = sizeof array / sizeof *array;

	sort(array, size);
	
	copy(array, array + size, ostream_iterator<int>(cout, " "));
}

问题5.5 非递归、无堆栈快速排序法

许多人都批评快速排序法，但观点却集中在快速排序法使用了递归的方法。但事实上这并不是快速排序法的最严重缺电。无论如何，写一个不用递归的快速排序法也可以让不少人安心，请问能不能写一个不用递归，但也不用堆栈的快速排序法来排正整数~

#include <iostream>
#include <algorithm>
#include <iterator>

using namespace std;

#define YES 1
#define NO 1
#define ALWAYS 1

#define SWAP(array, y) do { int t; t = array; array = y; y = t; } while (0);

const int size = 7;
int array[size] = {3, 2, 1, 6, 4, 7, 5};

void sort(int (&array)[size], int size)
{
	if (array == NULL || size <= 0)
		return;

	int sorted;
	int split;
	int next;
	int key;

	for (sorted = 0; sorted < size; sorted++)
	{
		while (array[sorted] > 0)
		{
			key = array[sorted];
			split = sorted;
			for (next = sorted + 1; array[next] > 0; next++)
			{
				if (array[next] < key)
				{
					split++;
					SWAP(array[split], array[next]);
				}
			}
			SWAP(array[sorted], array[split]);
			array[split] = -array[split];
		}
		array[sorted] = -array[sorted];
		copy(array, array + size, ostream_iterator<int>(cout, " "));
		system("pause");
	}
}

void main()
{
	sort(array, size);
	copy(array, array + size, ostream_iterator<int>(cout, " "));
	cout << endl;
}

问题5.6 求中位数

一组数的中位数，就是把那一组数从小到大排好后位居中间的那一个；如果有奇数个，那么在中间的那一个是存在的，但若有偶数个，就没有中间的那一个数了，因此就取位于中间那两个数的平均数。例如，3, 1, 7, 5, 9经过排列后是1, 3, 5, 7, 9，所以中位数是5；但3, 1, 7, 5, 9, 4，经过排序得到1, 3, 4, 5, 7, 9，所以中位数就是(4+5)/2=4，为了方便用整数运算，请写一个程序，接收一个整数数组，不必排大小而找出该数组的中位数。

思路：利用partition操作来完成此题！

问题5.7 堆积法

请写一个堆积排序法的程序，可以参考任何手头上的书籍，但注意一点，即程序必须写得有效率

思路：堆排序写N遍了，不想再写了~

程序猿最拿手的是神马??? COPY！！！

#include <iostream>
#include <algorithm>
#include <iterator>

using namespace std;

#define YES 1
#define NO 0

void fix_heap(int *, int, int, int);

void sort(int *old_x, int n)
{
	int *x = old_x - 1;
	int temp;
	int size, i;

	for (i = n / 2; i >= 1; i--)
		fix_heap(x, i, x[i], n);

	for (size = n; size >= 2; size--)
	{
		temp = x[1];
		fix_heap(x, 1, x[size], size - 1);
		x[size] = temp;
	}
}

void fix_heap(int *x, int root, int key, int bound)
{
	int father, son;
	int done;

	father = root;
	son = father + father;
	done = NO;
	while (son <= bound && !done)
	{
		if (son < bound && x[son + 1] > x[son])
			son++;
		if (key < x[son])
		{
			x[father] = x[son];
			father = son;
		}
		else
			done = YES;
		son = father + father;
	}
	x[father] = key;
}

void main()
{
	const int size = 7;
	int array[size] = {3, 2, 1, 6, 4, 7, 5};

	sort(array, size);
	copy(array, array + size, ostream_iterator<int>(cout, " "));
}

堆排序的另一种更好的写法：

#include <iostream>
#include <string>
#include <iterator>
#include <algorithm>

using namespace std;

void fix_heap(int *array, int size, int index)
{
	if (array == NULL || size <= 0)
		return;

	int key = array[index];
	
	while (index < size)
	{
		int leftChild = index * 2;
		int rightChild = index * 2 + 1;
		int bigIndex = index;

		if (leftChild <= size && array[bigIndex] < array[leftChild])
			bigIndex = leftChild;
		if (rightChild <= size && array[bigIndex] < array[rightChild])
			bigIndex = rightChild;

		if (bigIndex != index)
		{
			swap(array[index], array[bigIndex]);
			index = bigIndex;
		}
		else
		{
			break;
		}
	}
}

void sort(int *array, int size)
{
	if (array == NULL || size <= 0)
		return;

	int *x = array - 1;

	for (int i = size / 2; i >= 1; i--)
	{
		fix_heap(x, size, i);
	}
	
	for (int i = size; i >= 1; i--)
	{
		fix_heap(x, i, 1);
		swap(x[i], x[1]);
	}
}

void main()  
{  
	const int size = 7;  
	int array[size] = {3, 2, 1, 6, 4, 7, 5};  

	sort(array, size);  
	copy(array, array + size, ostream_iterator<int>(cout, " "));  
} 

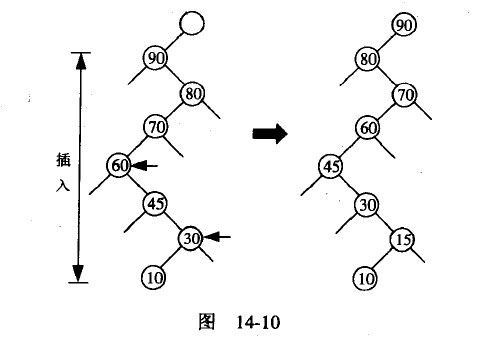
问题5.8 改良的堆积法

在用堆积法排序时会有一个明显的缺点，许多优秀的程序员可能都会看出来。如果现在要决定x[i]是不是应该在目前的位置，要找出在堆积中x[i]的两个后代，x[2*i]与x[2*i+1]，再用这两者中大的一个与x[i]相比，如果x[i]比较大，问题就解决了；但若x[i]比较小，就把x[2*i]与x[2*i+1]中大的那个与x[i]互换，再去处理在新位置的x[i]值。很明显，把一个值每往下移一层就需要两次比较，是不是太多了一点？请发展一项技巧来克服这个短处~

思路：下面的图。。。

#include <iostream>
#include <algorithm>
#include <iterator>

using namespace std;

#define YES 1
#define NO 0

void fix_heap(int *, int, int, int);

void sort(int *old_x, int n)
{
	int *x = old_x - 1;
	int temp;
	int size, i;

	for (i = n / 2; i >= 1; i--)
		fix_heap(x, i, x[i], n);

	for (size = n - 1; size >= 1; size--)
	{
		temp = x[size + 1];
		x[size + 1] = x[1];
		fix_heap(x, 1, temp, size);
	}
}

void fix_heap(int *x, int root, int key, int bound)
{
	int son, level;
	int top, bottom, mid;

	son = root + root;
	level = 1;
	for (; son < bound; level++)
		son = (x[son] < x[son + 1] ? (son + 1) << 1 : son << 1);
	if (son > bound)
		level--, son >>= 1;
	top = level;
	bottom = 0;
	while (top > bottom)
	{
		mid = (top + bottom) / 2;
		if (key <= x[son >> mid])
			top = mid;
		else
			bottom = mid + 1;
	}

	for (mid = level - 1; mid >= top; mid--)
		x[son >> (mid + 1)] = x[son >> mid];
	x[son >> top] = key;
}

void main()
{
	const int size = 7;
	int array[size] = {3, 2, 1, 6, 4, 7, 5};

	sort(array, size);
	copy(array, array + size, ostream_iterator<int>(cout, " "));
}

问题5.9 合并法

有一个叫做合并排序法的技巧是这样的：把要排序的资料分成大约相等的两组，把这两组排序排好之后，通过合并的技巧而合成一个全部都排好的结果。请写一个程序来实现这个算法。

思路：归并排序写N次了~

问题5.10 桶子法

快速排序法、二分插入法、堆积法、合并法等，都至少需要用nlogn成正比的比较次数来排n个数据，当然不一定是数值。但如果要排的不过是一些正整数，有没有更快的办法？请利用所学的知识写出这个特殊的排序的程序，理想是打破nlogn的限制

思路：先按个位排序、再按十位排序、再按百位排序、再。。。

问题5.11 单一重复元素排序

如果一个数组中有n个元素，但并非每一个元素都不相同。事实上，只有大约alogn个值是不同的，其余n-alogn个值全部一样，请发展一个特别快的程序把数组的元素排好顺序。a是常数，为了方便起见，可以当成1；另外，n-alogn>0，而且n比alogn大很多，请问程序用了多少次比较？

思路：先找出那个重复的元素，然后只计入1次进行排序，排序之后再重新写入重复元素

#include <iostream>
#include <algorithm>
#include <iterator>

using namespace std;

#define YES 1
#define NO 0

void dup_sort(int *x, int n)
{
	int dup;
	int count, index, i, j;

	for (i = 1; i < n; i++)
	{
		if (x[i] == x[i - 1])
		{
			dup = x[i];
			break;
		}
	}
	
	for (count = i = 0; i < n; i++)
	{
		if (x[i] != dup)
			x[count++] = x[i];
	}

	x[count++] = dup;
	sort(x, x + count);

	for (index = n - 1, i = count - 1; i >= 0 && x[i] != dup; i--)
		x[index--] = x[i];
	if (i >= 0 && x[i] == dup)
		for (j = i + 1; j <= index; j++)
			x[j] = dup;
}

void main()
{
	int array[] = {3, 2, 1, 2, 6, 2, 4, 7, 2, 2, 5};
	const int size = sizeof array /sizeof *array;
	dup_sort(array, size);
	copy(array, array + size, ostream_iterator<int>(cout, " "));
}

问题5.12 均匀重复元素排序

如果一个数组有n个元素，但有alogn不同的值，换句话说，数组中有alogn不同的值，每一个都重复出现了n/alogn次。请写一个特别快的程序把数组的元素排好顺序。假设n很大，比alogn大很多，a是一个常数，请问程序用了多少次比较，为了方便起见，把a当成1

#include <iostream>
#include <algorithm>
#include <iterator>
#include <cmath>

using namespace std;

#define MIN(x, y) (x) <= (y) ? (x) : (y)
#define SWAP(x, y) {int *t; t = x; x = y; y = t; }

int *in1_data, *in2_data, *out_data;
int *in1_count, *in2_count, *out_count;
int number;

int array[] = {3, 4, 3, 2, 1, 3, 1, 1, 4, 3, 2, 2, 4, 2, 1, 4};
const int size = sizeof array / sizeof *array;

void LOG_sort(int *, int);
int LOG_merge(int *, int, int);
int compress(int *, int, int *, int *);
void LOG_expand(int *);
void sort(int *, int);
int Partition(int *array, int start, int end);

void _QuickSort(int *array, int start, int end) {
	if(start < end) {
		int pivot = Partition(array, start, end);
		_QuickSort(array, start, pivot - 1);
		_QuickSort(array, pivot + 1, end);
	}
}

int Partition(int *array, int start, int end) {
	//别一个不小心写出 int pivot = array[end];
	int& pivot = array[end];
	int i = start - 1, j = start;

	while(j < end) {
		if(array[j] < pivot) {
			i++;
			swap(array[i], array[j]);
		}
		j++;
	}

	swap(array[i + 1], pivot);

	return i + 1;
}


void LOG_sort(int *array, int n)
{
	if (array == NULL || n <= 0)
		return;

	int log_n = (int)(log((double)n) + 0.5);
	int i;
	cout << "n = " << n << endl;
	cout << "log_n = " << log_n << endl;
	cout << "before sort" << endl;
	copy(array, array + n, ostream_iterator<int>(cout, " "));
	cout << endl;
	for (i = 0; i < n; i += log_n)
	{
		cout << "i = " << i << endl;
		cout << "i + min(log_n, n - i) = " << i + min(log_n, n - i) << endl;
		_QuickSort(array, i, i + min(log_n, n - i) - 1);
		for (int i = 0; i < n; i++)
			cout << array[i] << " ";
		cout << endl;
	}

	cout << "after sort" << endl;
	for (int i = 0; i < n; i++)
		cout << array[i] << " ";
	cout << endl;

	in1_data = (int *) malloc (sizeof(int) * log_n);
	in2_data = (int *) malloc (sizeof(int) * log_n);
	out_data = (int *) malloc (sizeof(int) * log_n);
	in1_count = (int *) malloc (sizeof(int) * log_n);
	in2_count = (int *) malloc (sizeof(int) * log_n);
	out_count = (int *) malloc (sizeof(int) * log_n);

	number = LOG_merge(array, n, log_n);
	LOG_expand(array);

/*
	free(in1_data);
	free(in2_data);
	free(out_data);
	free(in1_count);
	free(in2_count);
	free(out_count);*/
}

int LOG_merge(int *array, int n, int seg_size)
{
	if (array == NULL || n <= 0)
		return -1;

	int no1, no2;
	int start, len;
	int i, j, k;

	no1 = compress(array, seg_size, in1_data, in1_count);

	cout << "**************" << endl;
	for (int i = 0; i < no1; i++)
	{
		cout << in1_data[i] << " ";
	}
	cout << endl;
	cout << "**************" << endl;

	for (start = seg_size; start < n; start += len)
	{
		len = MIN(seg_size, n - start);
		no2 = compress(array + start, len, in2_data, in2_count);

		cout << "**************" << endl;
		for (int i = 0; i < no2; i++)
		{
			cout << in2_data[i] << " ";
		}
		cout << endl;
		cout << "**************" << endl;

		for (i = j = k = 0; i < no1 && j < no2;)
		{
			if (in1_data[i] < in2_data[j])
			{
				out_data[k] = in1_data[i];
				out_count[k] = in1_count[i];
				i++, k++;
			}
			else if (in1_data[i] > in2_data[j])
			{
				out_data[k] = in2_data[j];
				out_count[k] = in2_count[j];
				j++, k++;
			}
			else
			{
				out_data[k] = in1_data[i];
				out_count[k] = in1_count[i] + in2_count[j];
				i++, j++, k++;
			}
			cout << "!!!" << endl;
		}
		for (; i < no1; i++, k++)
		{
			out_data[k] = in1_data[i];
			out_count[k] = in1_count[i];
		}

		for (; j < no2; j++, k++)
		{
			out_data[k] = in2_data[j];
			out_count[k] = in2_count[j];
		}
		no1 = k;
		SWAP(in1_data, out_data);
		SWAP(in1_count, out_count);

		cout << "-------------------" << endl;
		cout << "k = " << k << endl;
		for (int i = 0; i < k; i++)
		{
			cout << "in" << in1_data[i] << " ";
			cout << "count" << in1_count[i] << " ";
		}
		cout << endl;
		cout << "-------------------" << endl;
	}

	return no1;
}

int compress(int *array, int n, int *data, int *count)
{
	int i;
	int no = 0;

	if (n == 0)
		return 0;
	else
	{
		data[0] = array[0];
		count[0] = 1;
		for (i = 1; i < n; i++)
		{
			if (array[i] == array[i - 1])
				count[no]++;
			else
			{
				data[++no] = array[i];
				count[no] = 1;
			}
		}
		no++;
		return no;
	}
}

void LOG_expand(int *array)
{
	int total;
	int i, j;

	for (total = i = 0; i < number; i++)
	{
		for (j = 0; j < in1_count[i]; j++)
		{
			array[total++] = in1_data[i];
		}
	}
}

void main()
{
	LOG_sort(array, size);
	for (int i = 0; i < size; i++)
		cout << array[i] << " ";
	cout << endl;
}

问题5.13 堆积式合并

已知m个数组，每一个数组都有n个元素，为了方便起见，这m个数组正好是x[][]矩阵中的m列。如果这m列中的元素都各自按照从小到大的顺序排列好了，请写一个程序把这m*n个合并到一个大矩阵去。不过在做这个题目时有进一步的限制，因为内存有限，大概最多只有与m成正比的内存可以使用。请问要如何克服这一层限制，当然程序的速度就会变慢了~

问题5.14 检查数组元素是否相异

已知一个数组，请写一个程序把相同的元素去掉而只留下一个

思路：利用快排先排序，之后就不说了，代码很简单，不写了~

问题5.15 数组中和为零的段落

一直一个整数数组，其中可能有正整数、负整数和0，而且元素也不会重复出现，请写一个程序找出这个数组中是否有一个子数组元素的和为0.所谓的子数组，就是原来数组中连续的若干个元素。例如，如果数组为1,2,3,-5,4，那么2,3,-5这个子数组中元素的和为0

思路：这是一道非常有意思的题，看下面的两个式子：

x1 + x2 = 0

x1 + x2 + x3 + x4 + x5 + x6 = 3

不难得出：x3 + x4 + x5 + x6 = 0

#include <iostream>
#include <algorithm>
#include <iterator>

using namespace std;

#define YES 1
#define NO 0

int zero_sum(int *x, int n)
{
	int i;

	for (i = 1; i < n; i++)
		x[i] += x[i - 1];

	sort(x, x + n);
	for (i = 1; i < n && x[i] != x[i - 1]; i++)
		;
	return (i == n) ? NO : YES;
}

void main()
{
	int array[] = {4, -1, 2, 1, -2, -1, 5};
	const int size = sizeof array / sizeof *array;

	int result = zero_sum(array, size);
	if (result == YES)
		cout << "exist" << endl;
	else
		cout << "not exist" << endl;
}

如果要求出具体序列，则需要用稳定的排序算法排序，而且用一个结构体保存好下标index~对这个结构体排序

问题5.16 平面上的极大点

在平面上如果有两个点(x, y)与(a, b)，说(x, y)支配了(a, b)，这就是指x >= a而且y >= b；用图来看就是(a,b)坐落在以(x, y)为右上角的一个无限的区域中。对于平面上的任意一个有限点集合而言，一定存在若干个点，它们不会被集合中任何一个点所支配，这些点就构成一个所谓的极大集合。请写一个程序，读入一个新的集合（以(x,y)的坐标形式），找出这个集合中的极大集合。

问题5.17 宴会中访问数目的极大值

在一个宴会中一共有n位来宾，依照来宾的到达和离去的登记时间，知道第i位来宾在xi时到达，在yi时离开，因此第i位来宾在宴会场中的时间是[xi, yi)，亦即xi <= t <= yi中所有可能的t，请写一个程序，读入xi与yi，1<=i<=n，找出同一时刻之内最多会有多少人同时在宴会场中。

思路：按时间排序，如果out和in是同时的，那么out在前，in在后

代码比较简单，原封不动的copy：

#include <iostream>
#include <algorithm>
#include <iterator>

using namespace std;

#define IN 1
#define OUT 0

struct table
{
	int clock;
	int status;
};

typedef struct table TABLE;

void sort(TABLE *, int);
void qsort(TABLE *, int, int);
void split(TABLE *, int, int, int *);
void swap(TABLE *, TABLE*);

int max_visitors(int *x, int *y, int n)
{
	if (x == NULL || y == NULL || n <= 0)
		return -1;

	TABLE *time_table;
	int max_count;
	int count;
	int i;

	time_table = (TABLE *) malloc (sizeof(TABLE) * (2 * n));

	for (i = 0; i < n; i++)
	{
		(time_table + i)->clock = x[i];
		(time_table + i)->status = IN;
	}

	for (i = 0; i < n; i++)
	{
		(time_table + i + n)->clock = y[i];
		(time_table + i + n)->status = OUT;
	}

	sort(time_table, time_table + 2 * n);

	for (max_count = count = i = 0; i < 2 * n; i++)
	{
		if ((time_table + i)->status == OUT)
			count--;
		else
		{
			count++;
			max_count = (max_count < count) ? count : max_count;
		}
	}

	free(time_table);
	return max_count;
}

void sort(TABLE *x, int n)
{
	int first = 0;
	int last = n - 1;
	qsort(x, first, last);
}

void qsort(TABLE *x, int first, int last)
{
	int split_point;

	if (first < last)
	{
		split(x, first, last, &split_point);
		if (split_point - first < last - split_point)
		{
			qsort(x, first, split_point - 1);
			qsort(x, split_point + 1, last);
		}
		else
		{
			qsort(x, split_point + 1, last);
			qsort(x, first, split_point - 1);
		}
	}
}

void split(TABLE *x, int first, int last, int *split_point)
{
	int current_split, next;
	int temp;

	temp = x[first].clock;
	current_split = first;
	for (next = first + 1; next <= last; next++)
	{
		if (x[next].clock < temp || (x[next].clock == temp && x[next].status == OUT))
		{
			current_split++;
			swap(&x[current_split], &x[next]);
		}
	}
	swap(&x[first], &x[current_split]);
	*split_point = current_split;
}

void swap(TABLE *p, TABLE *q)
{
	int temp;

	temp = p->clock;
	p->clock = q->clock;
	q->clock = temp;
}

问题5.18 包含在其他区间中的区间

已知一组区间[ai, bi]，i = 1, 2, ..., n;请写一个程序，找出这些区间中有哪些会包含在其他的区间中~