双线性插值(Bilinear interpolation)的图像拉伸在mobile上面的实现
双线性插值(Bilinear interpolation)的图像拉伸在mobile上面的实现
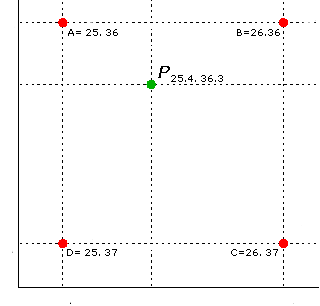
双线性插值简单的说,就是扩展了之后的图像像素坐标映射回原来的坐标空间的时候, 如果出现了没有对应到整数点的情况。这时候需要做2次线性的插值计算出新的坐标的像素值,比如说:
这里可以看到这个P点落在了ABCD区间内, 如果我们本着最朴素的这个P点最靠近谁权重就越大的加权平均的思想, 我们很容易得到这样的论断:
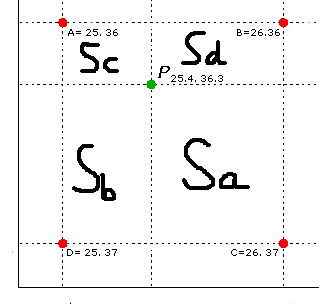
A点对P的影响就是Sa的面积, B点的影响就是Sb, C点就Sc, d就是Sd。这样越近就是权重越大,基本上就是这样的逻辑。
这样P的像素可以简单的用 (A*Sa+B*Sb+C*Sc+D*Sd )/(Sa+Sb+Sc+Sd);来得到了。如下的代码:
view plaincopy to clipboardprint?
/**
** method to remove sharp the raw image with unsharp mask
* @param src input grayscale binary array
* @param dst output grayscale result, the memory need to be allocated outside of the function
* @param srcWidth width of the input grayscale image
* @param srcHeight height of the input grayscale image
* @param scalePercent, scale percentage (0-xxx)
*/
void stretchImage (const unsigned char* src, unsigned char* dst, int srcWidth, int srcHeight, int scalePercent)
{
if (scalePercent < 0)
return;
int x, y;
int ox, oy;
int tmpx,tmpy;
int ratio = (100 << 8)/scalePercent;
int dstWidth = srcWidth * scalePercent / 100;
int dstHeight = srcHeight * scalePercent / 100;
unsigned char color[2][2];
for (int j = 0; j < dstHeight; j ++)
{
for (int i = 0; i < dstWidth; i ++)
{
tmpx = i * ratio;
tmpy = j * ratio;
ox = tmpx >> 8;
oy = tmpy >> 8;
x = tmpx & 0xFF;
y = tmpy & 0xFF;
color[0][0] = src[ oy*srcWidth + ox ];
color[1][0] = src[ oy*srcWidth + ox +1 ];
color[0][1] = src[ (oy+1)*srcWidth + ox ];
color[1][1] = src[ (oy+1)*srcWidth + ox+1 ];
int final = (0x100 - x)*(0x100 - y)*color[0][0] + x*(0x100 - y)*color[1][0] + (0x100-x)*y*color[0][1] + x*y*color[1][1];
final = final >> 16;
if (final>255)
final = 255;
if (final<0)
final = 0;
dst [ j*dstWidth + i] = (unsigned char)final;
}
}
}
需要说明的事情是, 浮点数需要引入效率上一定的损失, 当然我们这里就用大数来和谐。但是只是随便写写的代码, 我们没有加入超出int范围的检查或者说明,暂时也只能这样了:)。用了这个函数的效果还是不错的, 我们来看看在75%,125%和250%时候的效果:
原图:
%75效果图:
125%效果图:
250%效果图:
其实从效果图多少可以看出一些的问题就是, 随着图像的拉伸, 图像的锐度其实降低了, 这个比较容易想象的,因为我们这个拉伸的办法本身就是线性的,无疑来扩大的时候把锐利的边缘模糊化了,所以自然在图像扩大很多倍的时候效果不是很好了。
本文来自CSDN博客,转载请标明出处:http://blog.csdn.net/hhygcy/archive/2009/08/11/4434870.aspx