全排列问题

全排列在笔试面试中很热门，因为它难度适中，既可以考察递归实现，又能进一步考察非递归的实现，便于区分出考生的水平。所以在百度和迅雷的校园招聘以及程序员和软件设计师的考试中都考到了，因此本文对全排列作下总结帮助大家更好的学习和理解。对本文有任何补充之处，欢迎大家指出。

首先来看看题目是如何要求的（百度迅雷校招笔试题）。

用C++写一个函数, 如 Foo(const char *str), 打印出 str 的全排列,
如 abc 的全排列: abc, acb, bca, dac, cab, cba

 

一．全排列的递归实现

为方便起见，用123来示例下。123的全排列有123、132、213、231、312、321这六种。首先考虑213和321这二个数是如何得出的。显然这二个都是123中的1与后面两数交换得到的。然后可以将123的第二个数和每三个数交换得到132。同理可以根据213和321来得231和312。因此可以知道——全排列就是从第一个数字起每个数分别与它后面的数字交换。找到这个规律后，递归的代码就很容易写出来了：

//全排列的递归实现
#include <stdio.h>
#include <string.h>
void Swap(char *a, char *b)
{
    char t = *a;
    *a = *b;
    *b = t;
}
//k表示当前选取到第几个数,m表示共有多少数.
void AllRange(char *pszStr, int k, int m)
{
    if (k == m)
    {
        static int s_i = 1;
        printf("  第%3d个排列\t%s\n", s_i++, pszStr);
    }
    else
    {
        for (int i = k; i <= m; i++) //第i个数分别与它后面的数字交换就能得到新的排列
        {
            Swap(pszStr + k, pszStr + i);
            AllRange(pszStr, k + 1, m);
            Swap(pszStr + k, pszStr + i);
        }
    }
}
void Foo(char *pszStr)
{
    AllRange(pszStr, 0, strlen(pszStr) - 1);
}
int main()
{
    printf("         全排列的递归实现\n");
    printf("  --by MoreWindows( http://blog.csdn.net/MoreWindows )--\n\n");
    char szTextStr[] = "123";
    printf("%s的全排列如下:\n", szTextStr);
    Foo(szTextStr);
    return 0;
}

//全排列的递归实现
#include <stdio.h>
#include <string.h>
void Swap(char *a, char *b)
{
	char t = *a;
	*a = *b;
	*b = t;
}
//k表示当前选取到第几个数,m表示共有多少数.
void AllRange(char *pszStr, int k, int m)
{
	if (k == m)
	{
		static int s_i = 1;
		printf("  第%3d个排列\t%s\n", s_i++, pszStr);
	}
	else
	{
		for (int i = k; i <= m; i++) //第i个数分别与它后面的数字交换就能得到新的排列
		{
			Swap(pszStr + k, pszStr + i);
			AllRange(pszStr, k + 1, m);
			Swap(pszStr + k, pszStr + i);
		}
	}
}
void Foo(char *pszStr)
{
	AllRange(pszStr, 0, strlen(pszStr) - 1);
}
int main()
{
	printf("         全排列的递归实现\n");
	printf("  --by MoreWindows( http://blog.csdn.net/MoreWindows )--\n\n");
	char szTextStr[] = "123";
	printf("%s的全排列如下:\n", szTextStr);
	Foo(szTextStr);
	return 0;
}

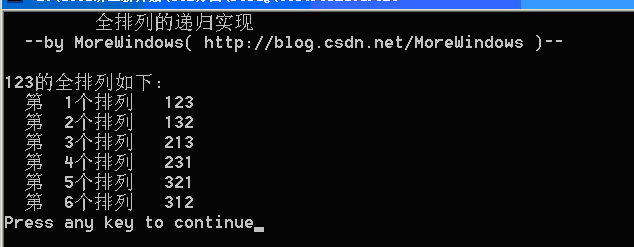
运行结果如下：

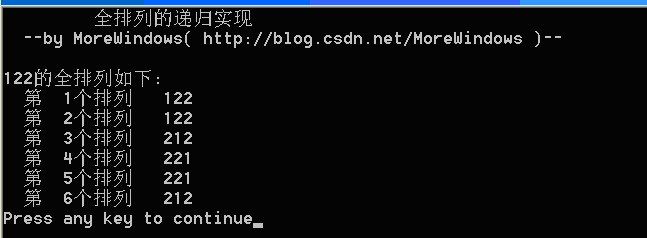
注意这样的方法没有考虑到重复数字，如122将会输出：

这种输出绝对不符合要求，因此现在要想办法来去掉重复的数列。

 

二．去掉重复的全排列的递归实现

由于全排列就是从第一个数字起每个数分别与它后面的数字交换。我们先尝试加个这样的判断——如果一个数与后面的数字相同那么这二个数就不交换了。如122，第一个数与后面交换得212、221。然后122中第二数就不用与第三个数交换了，但对212，它第二个数与第三个数是不相同的，交换之后得到221。与由122中第一个数与第三个数交换所得的221重复了。所以这个方法不行。

换种思维，对122，第一个数1与第二个数2交换得到212，然后考虑第一个数1与第三个数2交换，此时由于第三个数等于第二个数，所以第一个数不再与第三个数交换。再考虑212，它的第二个数与第三个数交换可以得到解决221。此时全排列生成完毕。

这样我们也得到了在全排列中去掉重复的规则——去重的全排列就是从第一个数字起每个数分别与它后面非重复出现的数字交换。用编程的话描述就是第i个数与第j个数交换时，要求[i,j)中没有与第j个数相等的数。下面给出完整代码：

//去重全排列的递归实现
#include <stdio.h>
#include <string.h>
void Swap(char *a, char *b)
{
    char t = *a;
    *a = *b;
    *b = t;
}
//在pszStr数组中，[nBegin,nEnd)中是否有数字与下标为nEnd的数字相等
bool IsSwap(char *pszStr, int nBegin, int nEnd)
{
    for (int i = nBegin; i < nEnd; i++)
        if (pszStr[i] == pszStr[nEnd])
            return false;
    return true;
}
//k表示当前选取到第几个数,m表示共有多少数.
void AllRange(char *pszStr, int k, int m)
{
    if (k == m)
    {
        static int s_i = 1;
        printf("  第%3d个排列\t%s\n", s_i++, pszStr);
    }
    else
    {
        for (int i = k; i <= m; i++) //第i个数分别与它后面的数字交换就能得到新的排列
        {
            if (IsSwap(pszStr, k, i))
            {
                Swap(pszStr + k, pszStr + i);
                AllRange(pszStr, k + 1, m);
                Swap(pszStr + k, pszStr + i);
            }
        }
    }
}
void Foo(char *pszStr)
{
    AllRange(pszStr, 0, strlen(pszStr) - 1);
}
int main()
{
    printf("         去重全排列的递归实现\n");
    printf("  --by MoreWindows( http://blog.csdn.net/MoreWindows )--\n\n");
    char szTextStr[] = "122";
    printf("%s的全排列如下:\n", szTextStr);
    Foo(szTextStr);
    return 0;
}

//去重全排列的递归实现
#include <stdio.h>
#include <string.h>
void Swap(char *a, char *b)
{
	char t = *a;
	*a = *b;
	*b = t;
}
//在pszStr数组中，[nBegin,nEnd)中是否有数字与下标为nEnd的数字相等
bool IsSwap(char *pszStr, int nBegin, int nEnd)
{
	for (int i = nBegin; i < nEnd; i++)
		if (pszStr[i] == pszStr[nEnd])
			return false;
	return true;
}
//k表示当前选取到第几个数,m表示共有多少数.
void AllRange(char *pszStr, int k, int m)
{
	if (k == m)
	{
		static int s_i = 1;
		printf("  第%3d个排列\t%s\n", s_i++, pszStr);
	}
	else
	{
		for (int i = k; i <= m; i++) //第i个数分别与它后面的数字交换就能得到新的排列
		{
			if (IsSwap(pszStr, k, i))
			{
				Swap(pszStr + k, pszStr + i);
				AllRange(pszStr, k + 1, m);
				Swap(pszStr + k, pszStr + i);
			}
		}
	}
}
void Foo(char *pszStr)
{
	AllRange(pszStr, 0, strlen(pszStr) - 1);
}
int main()
{
	printf("         去重全排列的递归实现\n");
	printf("  --by MoreWindows( http://blog.csdn.net/MoreWindows )--\n\n");
	char szTextStr[] = "122";
	printf("%s的全排列如下:\n", szTextStr);
	Foo(szTextStr);
	return 0;
}

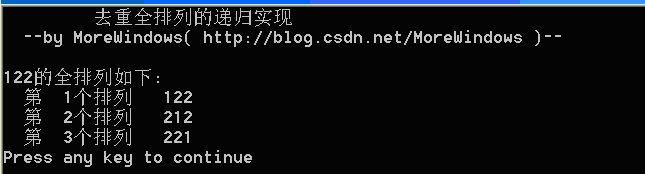
运行结果如下：

 

OK，到现在我们已经能熟练写出递归的方法了，并且考虑了字符串中的重复数据可能引发的重复数列问题。那么如何使用非递归的方法来得到全排列了？

 

三．全排列的非递归实现

要考虑全排列的非递归实现，先来考虑如何计算字符串的下一个排列。如"1234"的下一个排列就是"1243"。只要对字符串反复求出下一个排列，全排列的也就迎刃而解了。

我们可以借助于STL中的next_permutation（）函数来获得字典序的升序排列（也可以通过prev_permutation实现字典序的降序排列）

根据<<STL源码剖析>>中P380：next_permutation的实现过程如下：

         首先，从最尾端开始往前寻找两个相邻的元素，令第一个元素是i, 第二个元素是ii,且满足i<ii；

         然后，再从最尾端开始往前搜索，找出第一个大于i的元素，设其为j；

         然后，将i和j对调，再将ii及其后面的所有元素反转。

         这样得到的新序列就是“下一个排列”。

         我们以0,1,2,3,4为例来演示下next_permutation

详细的源码可以参照《STL源码剖析》

代码示例：

#include <iostream>  
#include <algorithm>  
using namespace std;  
  
void permutation(char* str,int length)  
{  
    sort(str,str+length);  
    do  
    {  
        for(int i=0;i<length;i++)  
            cout<<str[i];  
        cout<<endl;  
    }while(next_permutation(str,str+length));  
  
}  
int main(void)  
{  
    char str[] = "acb";  
    cout<<str<<"所有全排列的结果为："<<endl;  
    permutation(str,3);  
    system("pause");  
    return 0;  
}