PI control model----PID controlor

仅仅是P控制的话有还是有缺憾的，静差永远无法消除，系数小的时候静差大，系数大的时候稳定性差

因此想办法要改进P控制器，于是，加入I控制器，形成PI控制器

I on the accumulation of past errors——维基百科

利用对以往误差的积分实现消除静差！

% Code writer：EOF
% Time ： 2013.09.23 In XTU
% 
% This code just used for understand how PID work .So you may not to be
% intertwind with this code how to work!

% Matlab language is not like the C language which is strict to detail of a
% description of  problems

% What I want to say is that you should understand what is PID and then
% program it
clear all
clc

syms s
hold on
%% abstract the object which is controled into a function 1/(s^2+3*s+1)
num = 1;
den = sym2poly(s^2+3*s+1);
G = tf(num,den);

%% Set up the coefficient
%--------------------------
H = 1;%THE TARGET VALUE!!
%--------------------------
% PID系数
Kp = 20;% coefficient of  PID
Ki = 1;
Kd = 0;
%% Set up the coefficient controlor
C = pid(Kp,Ki,Kd);% set up a PID controlor
T = feedback(C*G,H);%backforward loop

step(T)

Kp = 20;% coefficient of  PID
Ki = 10;
Kd = 0;

C = pid(Kp,Ki,Kd);% set up a PID controlor
T = feedback(C*G,H);%backforward loop

step(T)

首先观察Kp = 20，Ki = 1和Kp = 20，Ki = 10这两条曲线，相比较而言，前者pi比例是20:1，后者是2:1

很明显，在比例作用大的蓝色曲线中任然存在静差，但是相对而言，过调的程度要小

在积分作用相对而言大的绿色曲线中，过调虽然严重（相对而言），但是很好的消除了静差

于是有，在一定范围内，Kp ，Ki的比例值从大减小的时候输出稳定性减弱，但是静差缩小

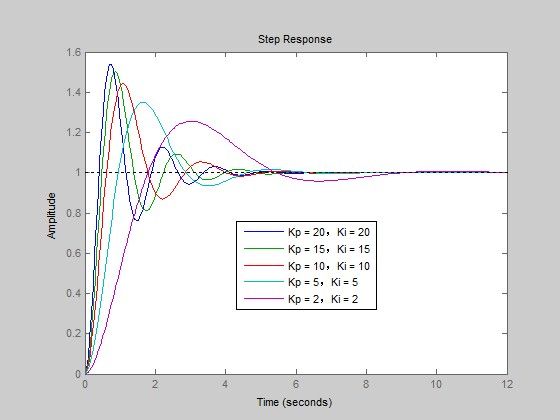
下面探讨Kp ，Ki比例相同的情况下，Kp或者Ki'值变化的情况

可以发现，在比值不变的的情况下，随着Kp（或者Ki）的增大，过调的现象越来越严重，波动频繁，但是稳定时间缩短

反而言之，在比值不变的的情况下，随着Kp（或者Ki）的减小，过调的现象越来越小，波动频率减小，但是稳定时间增长（如图紫色曲线的稳定时间是最长的）

根据整定口诀，可以对参数进行调整，然后得到好的曲线输出

最后看看stephen怎么说

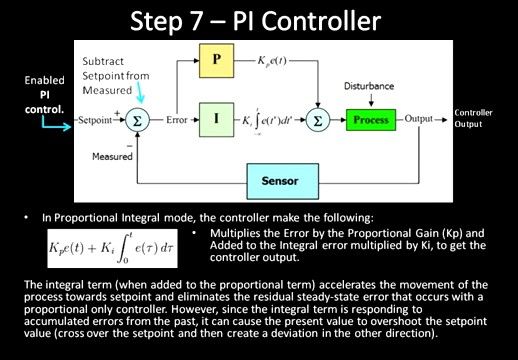
大意：PI模型就是将误差与比例系数Kp相乘，然后加上，误差对时间的积分乘以积分系数Ki，将得到的结果作为控制输出

PI模型中的积分项加速了输出向参考期望值靠近，消除了在仅有P控制的模型中产生的静差

然而，因为积分项是对过去误差的积分，它能产生过调

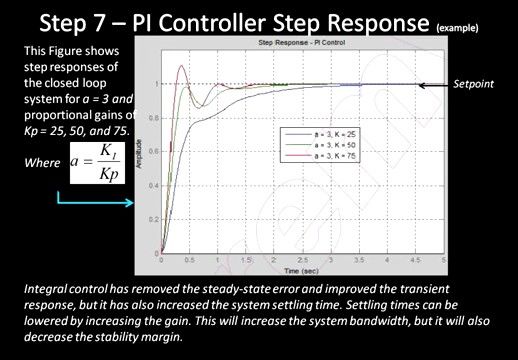
（我认为，这里其实应该加上一句话，当Pi系数比较大的时候才会产生过调）

积分控制器消除了静差，提升了暂态响应，但是他同样增加了系统的从开始到稳定的时间

而这段时间是可以通过增加Pi系数来减小的。同样，这又会增加系统的波动带宽，降低了稳定性输出