极小化极大算法与负极大值算法

1.极小化极大算法（Minimax）

     Minimax算法又名极小化极大算法，是一种找出失败的最大可能性中的最小值的算法。Minimax算法常用于棋类等由两方较量的游戏和程序，这类程序由两个游戏者轮流，每次执行一个步骤。我们众所周知的五子棋、象棋等都属于这类程序，所以说Minimax算法是基于搜索的博弈算法的基础。该算法是一种零总和算法，即一方要在可选的选项中选择将其优势最大化的选择，而另一方则选择令对手优势最小化的方法。

 

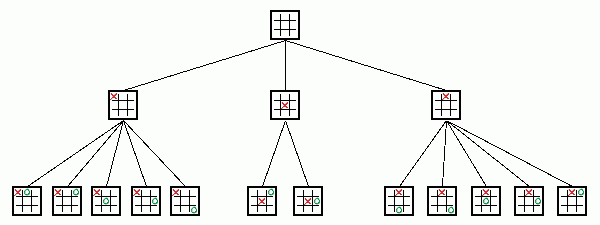
     我们知道，常用的博弈算法都是基于搜索的博弈算法，所有可能的下棋步骤构成一个树的结构，以Tic-tac-toe（中文称为井字棋，即两人轮流在井字棋盘的方格内划×或〇，谁先将划过的三个方格成一直线或对角线为胜）游戏为例，下面一幅图表示了Tic-tac-toe游戏的前两步所有可能的步骤.

     上图中第0层为空棋盘，第1层是×方所有可能的步骤，第2层是〇方所有可能的步骤。在第1层，×方需要选择使其优势最大的选择，而在第2层，〇方则需要选择使×方优势最小即己方优势最大的选择。

 

     Minimax的含义就是极小化对手的最大利益，在上图中，在第2层〇方一定会选择使自己优势最大的选择，而对于×方需要做的就是选择〇方最大选择中的极小值。

 

Minimax是一种深度优先搜索，其用伪代码表示如下：

function minimax(node, depth) if node is a terminal node or depth = 0 return the heuristic value of node if the adversary is to play at node let α := +∞ foreach child of node α := min(α, minimax(child, depth-1)) else {we are to play at node} let α := -∞ foreach child of node α := max(α, minimax(child, depth-1)) return α。

 

2.负极大值算法（Negamax）

负极大值算法是极小化极大算法的一个变体，其基本原理是基于下面的公式：

                                  max (a,b) = - min ( - a, - b)

    即在几个节点中选择得分最小的节点相当于将这些节点的得分乘以-1然后取得分最大的节点。这样Negamax算法就将每一步递归过程都统一了起来，每一次递归都选取最大值。

下面是Negamax算法的伪代码：

function negamax(node, depth) if node is a terminal node or depth = 0 return the heuristic value of node let best := -∞ foreach child of node best := max(α, -negamax(child, depth-1)) return best

 

3.两种的区别

     我们把电脑方的价值总和叫做CpValue，对手方价值总和叫做OpValue，那么一个局面的估值Value就是电脑方和对手方的价值差。表达如下式：Value=CpValue - OpValue。这个Value也就是最终返回给搜索引擎的估值。在基本的极小极大搜索的过程里估值的取得是和上式完全契合的，即无论任何时候取估值均由固定一方的值减去另一方的值。

 

而在负极大值形式的搜索中，
1.对于电脑方走棋所形成的局面，如果该节点是叶节点，则估值是CpValue - OpValue；如果该节点有父节点，则父节点必然是对手方走棋的局面，它是取极大值极点，我们希望取OpValue - CpValue中的最大的子节点。
2.对于对手方走棋所形成的局面，如果该节点是叶节点，则估值是OpValue - CpValue；如果该节点有父节点，则必然是电脑方走棋的局面，它是取极小值节点，我们希望取CpValue - OpValue中最大的子节点。
这样我们就理解了在负极大值算法中的那个负号啦。