Slice Smapling算法
今天看到一种新的Sampling技术,颇为兴奋。配上adaptive rejection sampling, Gibbs抽样就可以“无敌”了。
大致说说Slice sampling的算法:
我们想从一个密度分布为f(x)的函数中抽样
初始化:任意选择x0,步长w
for i= 1:n
固定xi,在[0,f(xi)]区间上均匀抽样,得到yi
固定yi,在函数值大于yi的x区间({x: f(x)>g(yi)})均匀抽样。
重复步骤,最后得到{xi,yi}的联合分布,从里面直接抽取到{xi}即得到x的边际模拟抽样结果。
上述算法实现的难点在第二步,如何从{x: f(x)>g(yi)}上均匀抽样。一种简便的算法如下:
1.对于第i步的xi,任意选取包含xi的长度为w的区间。
2.该区间的左右两个端点分别向左和向右延拓,知道端点的值都小于g(xi)
3.在上述区间中均匀抽样得到y,但是我们以一定概率接受它;如果g(y)<g(yi)则拒绝,以g(y)为新的端点重新抽样;如果g(y)>g(yi)则接受yi=y.
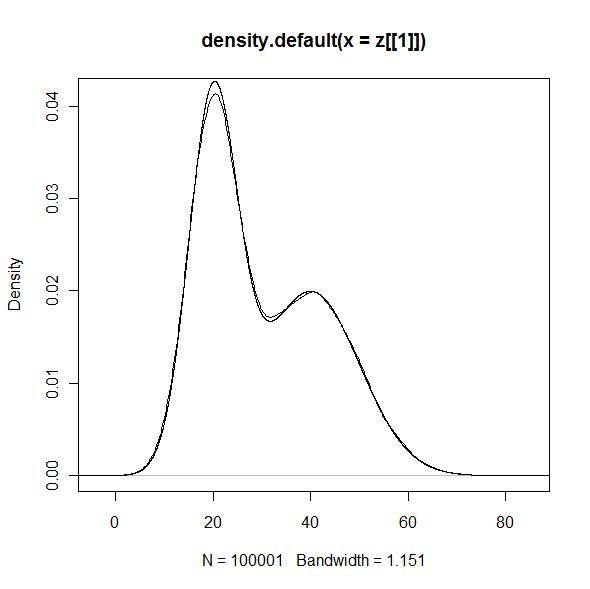
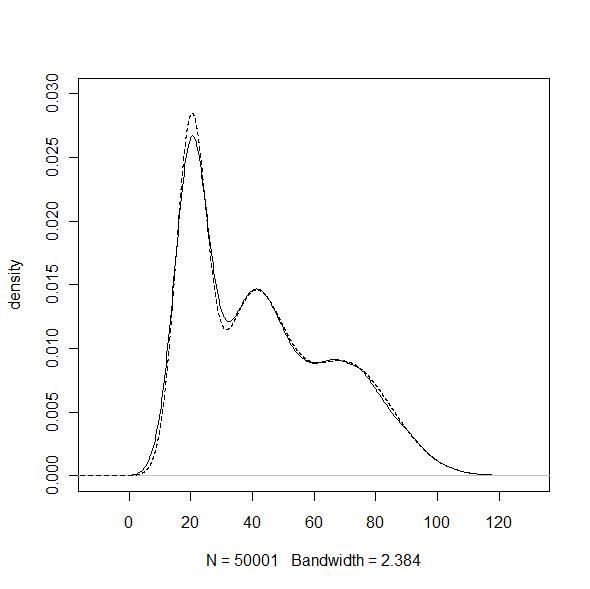
以下是我simulation的结果:
真实分布是一个高斯的混合分布,用slice sampling模拟的密度估计如图所示:
附代码(R):
p=function(x,u1,sig1,u2,sig2){
(1/3)*(1/(sqrt(2*pi)*15)*exp(-0.5*(x-70)^2/15^2)+1/(sqrt(2*pi)*sig1)*exp(-0.5*(x-u1)^2/sig1^2)+1/(sqrt(2*pi)*sig2)*exp(-0.5*(x-u2)^2/sig2^2))
}
sample=function(init,time,w,u1,sig1,u2,sig2){
X=NULL
Y=NULL
X[1]=init
for (i in 1:time){
Y[i]=runif(1,0,p(X[i],u1,sig1,u2,sig2))
xl=X[i]-runif(1,0,w)
xr=xl+w
while(!((p(xl,u1,sig1,u2,sig2)<Y[i])&(p(xr,u1,sig1,u2,sig2)<Y[i]))){
xl=xl-w
xr=xr+w
}
x=runif(1,xl,xr)
while(p(x,u1,sig1,u2,sig2)<Y[i]){
if(x>X[i]){xr=x}else{xl=x}
x=runif(1,xl,xr)
}
if(p(x,u1,sig1,u2,sig2)>Y[i]){X[i+1]=x} else{print('error')}
}
return(list(X,Y))
}
z=sample(20,50000,10,20,5,40,10)
plot(density(z[[1]]),ylim=c(0,0.03),ylab='density',main='')
x=seq(-100,100,0.01)
lines(x,p(x,20,5,40,10),lty=2)