viewstamp replication: A new primary copy method to support highly-avaliable d
为了提高服务能力或者服务稳定,往往需要把数据重复布署,也就是replication。重复带来的问题是,更新的时候会带来不一致。一种比较简单的方法是,在N台重复的机器里选一台作为主机,其他作备份,只能通过主机更新,主机更新完所有备机后,才向上层应用返回成功。如果主机故障,则从备机中挑一台作为新的主机,这需要用到选举算法。
这里存在几个问题,一是主机崩溃前的最后一个操作进行到哪了,二是网络分隔的时候,会选出多台主机,三是有的备机曾经发生过故障,上面的数据不是最新的,不能作为主机。
viewstampedreplication可以解决上面三个问题
view的含义是,可以互相联系的K台机器,以及主机ID,要求K大于集群中总机器数的一半。当有新的机器加入,或者有机器故障,或者更换主机,则变成另一个VIEW了。
必须一个VIEW中所有的机器都成功,该操作才算成功。VIEW中每台机器都记录最新一次操作的VIEWID及操作的时间戳。这样,就可以知道最后一个操作进行到哪了。因为K要求占大多数,所以不会出现多个VIEW。根据每台机器的记录,选择最新的一个,就可以知道哪些机器的数据不是最新的。
()Viewstamps算法
Viewstamps算法
1. 前言
Viewstamps算法是Oki和Liskov于1988年发表的论文,Liskov是一位计算机世界中杰出的女性,08年图灵奖得主、著名面向 对象五原则中“Liskov可替换原则”的提出者。我们已无精力考证Viewstamps是否是第一个多数派表决的算法,但知道其比 Paxos(1998)整整早了10年,杯具的是,随着06年googlechubby论文发表,Paxos迅速闻名于世,而Viewstamps依旧寂寂无闻。
2. 问题的由来
在分布式系统中一般通过复制来提高系统的可用性,而复制又引入了一致性的问题,比如我们把数据复制到A、B、C三个节点,如何保证A、B、C看到的复制数据的顺序是一致的?从深层次上来讲,复制节点就是一个状态机,我们有必要时刻保证各状态机状态的一致。
为了保证复制数据的一致性,Viewstamps采用了Primary-backup模式(类Master-slave),规定所有数据操作,无论是查询还是更新都必须通过primary进行,然后传递到各backup(显然primay-backup与数据库的master-slave还是不同 的,数据库的master-slave强调的是“单写多读”),这样,数据的一致性就得到了保证,但primary会成为单点,如果primary crash那进行一半的事务该如何处理?这正是viewstamps算法要解决的问题,所以viewstamps也经常被描述为master的选举算法。
3. 概念
- Primary Service被复制(部署)多份,每份复制称为backup,primary与众多的backup组成一个group,提供与一个primary相同的逻辑功能。
- group里的每个成员又被称为cohort,cohort可以是primary也可以是backup。
- group里的全部cohor又称为configuration,group更多是描述性的称呼,而configuration是指要在配置文件中把这个关系固定下来,是配置性的称呼。
- configuration中超过1/2的成员又称为多数派(majority),viewstamps允许2N+1个节点中的N个节点同时失败。
- 在某一时刻,系统的状态是有一个primary与几个backup提供服务(未必是所有的backup),这种状态称为view。
- 在某个primary或backup crash后,这个view就会被打破,从而形成新的view,这个过程叫view change,而viewstamps又自称为view change算法。
另外补充几个次重要概念:
- 每个group都有一个groupid,是配置好的,不能更改
- 每个view都有一个viewid,动态生成
- 每个cohort都有一个唯一的id
- 每个primary都有一个queue用来保证数据一致性,queue中的数据按照timestamp的顺序(先后顺序)保持数据
- primary每次与backup通信称为event
- 每个event必定发生在某个view中,event又是根据timestamps的顺序传递数据,因此算法叫viewstamps。
- 事务:viewstamps 中的事务实现方式都是二段提交,即prepare和commit两个阶段。
存在众多繁杂且表述不一的概念,也是viewstamps算法的一大特色,翻来覆去就那么几样东西,大家习惯即可。
4. 调用过程
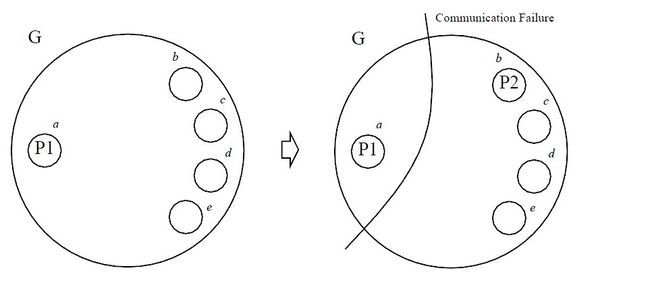
客户端C发送数据到primary,primary传播到backups,其图如下(其中(a=primary,b,c,d,e)构成一个group,a是primary): 图1
很显然,在a与b,c,d,e通信时,也称为发送event时,需要分布式事务,即等待b,c,d,e返回。如果parimary a crash,则会选举一个新的primary,如下图2:
primary并不是接收到event后立即同步到backup,而是在事务的prepare阶段集中处理。前面也提到过,event肯定是属于某个view,event是按timestamps的顺序发送,这样所有的event就会形成一个viewstamps的顺序。比如我们每个view的编号 即viewid都是全序的,即每次都会单调递增,每个event的顺序也是全序,这样每次primary接收到一个数据,都可转变为一个带全序的 event,可记录为<v1.1>,<v1.2>,<v2.1>,<v2.2>...因为一个事务可以提交多个数据最后一起提交,而服务端的view会随着cohort的crash而动态调整,因此客户端在与primary通信时都 需要指定哪个事务与primary的哪个view通信,而primary回复client生成的每个event的viewstamps,如下图3:
客户端和primary都记录这些数据,以准备后续的事务提交。当客户端准备提交时,在primary接收到prepare命令时,会把其上的viewstamp记录同步到backups上,因为viewstamp全序,就保证了这些事件会以相同的顺序在backups上执行,从而得到一个一致 的状态。为了保证这一点,单靠event状态一致是不够的,还必须要求backup不能跳号执行event,比如primary要求执 行<v2.3>,但backup发现<v2.2>尚未执行,则必须等<v2.2>执行完毕后才能执 行<v2.3>。
为什么会有<v2.2>尚未执行就有<v2.3>要求的情况呢?有两个原因:一是网络波动,信息传输有时差,但这在局域网中很少发生;二是backup可能会crash后苏醒,这个情况比较常见。
Primary在向backups复制数据时并不要求所有的backups都成功,而只是要求包含自己在内的一个多数派成功即可(在viewstamps算法中,称这样的多数派为sub-majority)。这点非常重要,详细说明如下:
假如在现在时刻viewstamps系统正常运行,其所有cohort成员是confirutaion的一个多数派,记为C;
系统在多次viewchange后仍能保持一个多数派,记为X
因为C、X都为多数派,因此C、X至少存在一个公共cohort,记为O,则cohort O知道系统在C中正常运行时的所有viewstamps,新的view可以根据O还原出viewchange前的所有工作状态,从而能为是否提交事务作出 决策。如果不能保证存在多数派,则无法保证viewstamps算法的正确性,也就是说在2N+1个节点中,最多允许N个节点失败。
5. 节点失败
cohort失败的情况比较多,但假定数据可以丢失、复制、乱序,但不能出现拜占庭问题,即不能篡改消息;另假设所有的失败都是fail-stop,即失败停止,不会在失败状态继续服务。虽然假设感觉比较多,但这些假设一般的通信环境都能满足。
节点会有下面几种失败状态:
- 失败导致service无法访问
- 失败后又苏醒,丢失之前的状态
- 网络失败导致分区,比如导致cohort被分成两组,组之内的cohort可以相互访问,组之间的不能,典型的发生场景是交换机发生问题。
前两种错误会导致view change;后一种失败因为采用强制多数派的机制,保证了虽然有一个少数派的网络存在,但因为无法形成多数派而无法工作,就杜绝了存在两个viewstamps group同时工作带来的风险。
一般我们会在cohort之间保持心跳检测,一旦某个cohort在指定的时间没有收到其他cohort的心跳则认为crash,从而发起view change。从理论上来说,通过心跳来检测对方server是否crash是不可靠的,主要是单凭心跳时间,无法区分crash和busy,这个值的设 定跟应用所处的网络环境有很大关系。当然也可引入其他更复杂的crash检测机制,就不在这里作深入讨论。
6. View change
如上所述,当某个cohort通过心跳发现对方已经crash时,就发起view change,可能会有多个cohort同时发起view change,所以必须保证只能建立一个新的view,基本方法如下:(假如A、B、C同时发现D失败)
1. A构造一个新的viewid,这个view id要比A所见到的所有的view id都大,并且不同的cohort生的view id一定不能相同,这点与paxos的proposalid非常像
2. A发送一个invitation到其他活着的cohort,比如X
3. X发现A发送的view id,比自己所见到的所有view id都大,于是接收邀请并回复给A;否则,X拒绝A,不做任何回应。
4. A在接收到多数派的回应后,认为新的view已经形成,初始化新的primary;否则,无法形成新的view,一段时间后改变view id重复上述过程
在4中只是说,接收到多数派的回应,就认为新的view已经形成,要达到这个目标必须满足两个充分条件:
- 存在一个多数派cohort接收了inviitation
- 并且这个多数派中至少存在一个cohort知道之前所有的viewstamp
第一个条件比较容易验证,因为在Viewstamps算法中假定viewstamps的记录没有持久化,所以第二个条件不总是成立,比如:
- 有A(primary)、B、C三个节点,A提交事务
- event同步到B但还未到C,A crash
- A又迅速从crash状态recovery
- B与A、C发生了网络分区
此时的现状是:A、C可以连通,但都没有viewstamps记录,所以无法形成新view;B有viewstamps记录,但无法与A、C互通,所以也无法形成新View。因此能否形成新view需要下面三个加强条件:
- a majority of cohorts accepted normally, or
- crash-viewid < normal-viewid, or
- crash-viewid = normal-viewid and the primary of view normal-viewid has done a normal acceptance of the invitation.
在形成新view后,还要继续:
5.A寻找新的primary,并把各cohort回应的viewstamp发送给primary初始化其状态,如果老的primary没有crash,可以继续指定为primary;否则随机指定cohort作为primary
6. 新Primary把在初始化时,把所有正确的viewstamp发送到所有的cohort,使所有的cohort状态一致。
整个过程大概如此。
7. 并发执行
在6中的过程可能有多个cohort同时执行,比如A、B同时进行view change,所以该问题本质上还是一个选举的问题,只是对于paxos来说,是多个proposer同时proposal选择最终决议,而现在是选择新的view。
在paxos算法中使用了2个phase解决选举的唯一性问题,而上述viewstamps的过程本质上就是paxos的phase 1,但仅凭phase1是无法达成最终决议,viewstamps 算法可能并没有意识到这一点,只是认为编号高的view会被最终选择,并提出了一些避免view change并发执行的方案。由此也可看出,paxos 算法理论上比viewstamps 更完善,也有更清晰的2phase的划分。
还有一个关键问题是view在算法过程中起了什么作用,如果没有view change而仅使用一个view是否可以?在原论文中作者提到了用view的原因:
Over time thecommunication capability within a group may change as cohorts or communicationlinks fail and recover. To reflect this changing situation, each cohort runs ina view.
就是说,因为节点、网络都会失败、恢复,为了反映这一情况每个节点需要运行在一个view中。
从实际应用情况来看,view反映的是节点某个时刻的运行快照,在每次新primary被选出时,需要使用正常的节点初始化其状态,但不需要所有正常节点的数据,只需要其最后一个view的viewstamps即可,如果仅采用一个view,就会每次把所有的数据都发送的新primary。
还有一种情况是网络失败,比如A、B、C三个节点,在发生网络分区,C与A、B隔离,经过一段时间网络分区修复,A、B、C又重新联通,但C上的数 据已经与A、B不一致,当再进行primary选举时就无法判断C上的数据是否可用。如果引入一个view,当C网络分区时,A、B会有新的 viewid,而分区修复时,根据viewid能明确区分出C上的数据不是最新数据。所以,引入view就是为节点引入了一个判断数据是否是最新的标志。
这也就证明了,在primary-backup模式中,当发生primary切换的时候,如果没有一定的分布式算法,仅靠backup上的数据是无 法保证新的primary能正确同步之前的状态,也就是说任何想仅通过backup去保证primary数据正确性的做法都是徒劳。
8. 优化
并不是每次cohort失败都需要导致view change,如果primary没有失败,而仅backup失败,且失败后的cohort仍能构成多数派,则无需view change。但primary失败则需要view change。viewchange的过程与primary是无关的,primary的指定也是随机的,那为什么primary失败缺要导致view change?其实primary切换需要2步工作:
- 准备primary切换后的数据,为cohort形成一个新的view
- 选择一个cohort作为primary
重要的是第一步工作,只要第一步完成了,选择哪个cohort作为primary都不是问题。所以,表面上primary与viewchange无关,其实view change的过程就是特为primary而准备。这样是viewstamps成为选举算法的原因。
9. 结论
Viewstams 并没有从理论上完整解决选举问题,但却为leader选举及选举后的leader状态同步提出了完整的方案。
相比而言,paxos理论上更完善,2 phase的表述也更清晰,但很显然的是viewstamps不完全等同与paxos,而只是做了paxos的phase 1。
Google chubby的人曾说,所有的分布式算法都是paxos的一个特例,信矣!