算法:求解AOE网的关键路径
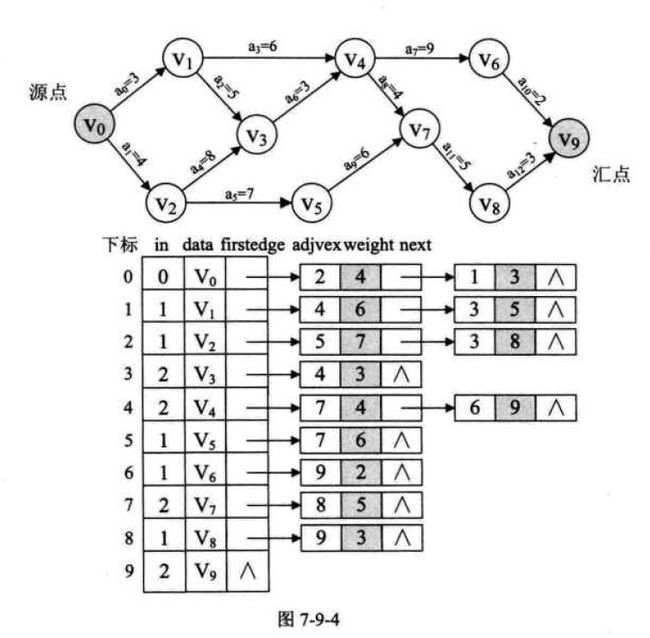
前面我们简要地介绍了AOE网和关键路径的一些概念,本文接着对求解关键路径程序的主要函数进行分析。现有一AOE网图如图7-9-4所示,我们使用邻接表存储结构,注意与拓扑排序时邻接表结构不同的地方在于,这里弧表结点增加了weight域,用来存储弧的权值。
求解事件的最早发生时间etv的过程,就是我们从头至尾找拓扑序列的过程,因此在求关键路径之前,需要先调用一次拓扑序列算法的代码来计算etv 和 拓扑序列列表,我们针对前面讲过的AOV网与拓扑排序的程序进行改进,代码如下(参考《大话数据结构》):
|
1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
/* 拓扑排序,若GL无回路,则输出拓扑排序序列并返回1,若有回路返回0。 */
bool TopologicalSort(GraphAdjList GL) { EdgeNode *pe; int i, k, gettop; int top = 0; /* 用于栈指针下标 */ int count = 0; /* 用于统计输出顶点的个数 */ /* 建栈将入度为0的顶点入栈 */ int *stack = ( int *)malloc(GL->numVertexes * sizeof( int)); for (i = 0; i < GL->numVertexes; i++) if ( 0 == GL->adjList[i].in) stack[++top] = i; /* 将入度为0的顶点入栈 */ top2 = 0; etv = ( int *)malloc(GL->numVertexes * sizeof( int)); for (i = 0; i < GL->numVertexes; i++) etv[i] = 0; /* 初始化 */ stack2 = ( int *)malloc(GL->numVertexes * sizeof( int)); cout << "TopologicalSort ..." << endl; while (top != 0) { gettop = stack[top--]; cout << GL->adjList[gettop].data << " -> "; count++; /* 输出i号顶点,并计数 */ stack2[++top2] = gettop; /* 将弹出的顶点序号压入拓扑序列的栈 */ for (pe = GL->adjList[gettop].firstedge; pe; pe = pe->next) { k = pe->adjvex; /* 将i号顶点的邻接点的入度减1,如果减1后为0,则入栈 */ if (!(--GL->adjList[k].in)) stack[++top] = k; /* 求各顶点事件的最早发生时间etv值 */ if ((etv[gettop] + pe->weight) > etv[k]) etv[k] = etv[gettop] + pe->weight; } } cout << endl; if (count < GL->numVertexes) return false; else return true; } |
int *etv,*ltv; /* 事件最早发生时间和最迟发生时间数组,全局变量 */
int *stack2; /* 用于存储拓扑序列的栈 */
int top2; /* 用于stack2的指针 */
其中stack2用来存储拓扑序列,以便后面求关键路径时使用。
上面的拓扑排序函数中除了增加了第12~19行,29行,38~39行,其他跟前面讲过的AOV网与拓扑排序没什么区别。
第12~19行初始化全局变量etv数组、top2和stack2的过程。第29行就是将本来要输出的拓扑序列压入全局栈stack2中。第38~39行很关键,是求etv数组的每一个元素的值,具体求值办法参见AOE网和关键路径。
下面来看求关键路径的算法代码。
|
1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
/* 求关键路径,GL为有向网,输出G的各项关键活动 */
void CriticalPath(GraphAdjList GL) { EdgeNode *pe; int i, j, k, gettop; int ete, lte; /* 声明活动最早发生时间和最迟发生时间变量 */ TopologicalSort(GL); /* 求拓扑序列,计算数组etv和stack2的值 */ ltv = ( int *)malloc(GL->numVertexes * sizeof( int)); /* 事件最早发生时间数组 */ for (i = 0; i < GL->numVertexes; i++) ltv[i] = etv[GL->numVertexes - 1]; /* 初始化 */ cout << "etv : "; for (i = 0; i < GL->numVertexes; i++) cout << etv[i] << ' '; cout << endl; while (top2 != 0) /* 出栈是求ltv */ { gettop = stack2[top2--]; /* 求各顶点事件的最迟发生时间ltv值 */ for (pe = GL->adjList[gettop].firstedge; pe; pe = pe->next) { k = pe->adjvex; if (ltv[k] - pe->weight < ltv[gettop]) ltv[gettop] = ltv[k] - pe->weight; } } cout << "ltv : "; for (i = 0; i < GL->numVertexes; i++) cout << ltv[i] << ' '; cout << endl; /* 求ete,lte和关键活动 */ for (j = 0; j < GL->numVertexes; j++) { for (pe = GL->adjList[j].firstedge; pe; pe = pe->next) { k = pe->adjvex; ete = etv[j]; /* 活动最早发生时间 */ lte = ltv[k] - pe->weight; /* 活动最迟发生时间 */ if (ete == lte) /* 两者相等即在关键路径上 */ cout << "<v" << GL->adjList[j].data << " - v" << GL->adjList[k].data << "> length: " << pe->weight << endl; } } } |
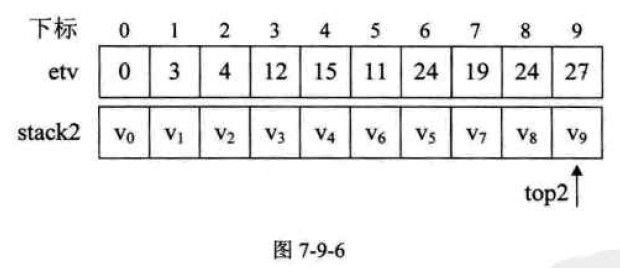
函数第7行调用求拓扑序列的函数,执行完毕后,全局数组etv和栈stack2 如图7-9-6所示,top2 = 10,也就是说,对于每个事件的最早发生时间,我们已经计算出来了。
第11~12行初始化全局变量ltv数组,因为etv[9] = 27,所以数组ltv值现在为全27。
第19~29行是计算ltv 数组的循环,具体方法参见AOE网和关键路径。
当程序执行到第36行,etv和ltv数组的值如图7-9-9
比如etv[1] = 3, 而ltv[1] = 7,表示如果单位是天的话,哪怕v1整个事件在第7天才开始,也可以保证整个工程的按期完成,可以提前v1事件开始时间,但最早也得第3天开始。
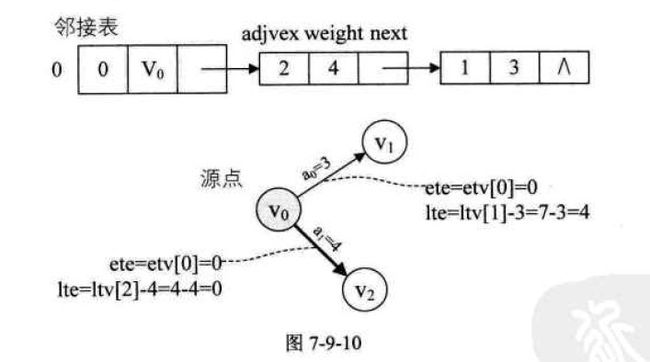
第36~47行是求另两个变量,活动最早开始时间ete和活动最晚开始时间lte,并对相同下标的它们进行比较。两重循环嵌套是对邻接表的顶点和每个顶点的弧表遍历,具体方法参见AOE网和关键路径,举例来说,如图7-9-10,当j = 0时,当k = 2, ete = lte, 表示
弧<v0, v2> 是关键路径,因此打印;当k = 1, ete != lte, 故弧<v0, v1> 不是关键路径。
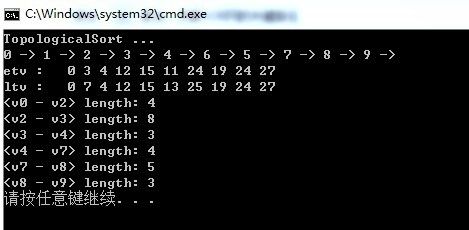
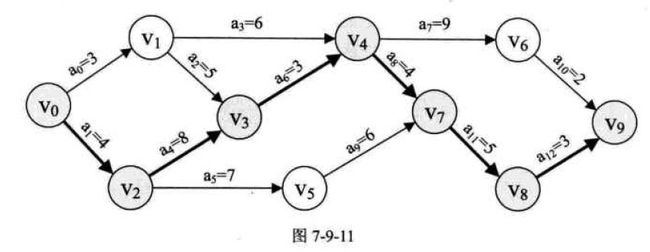
j = 1 一直到 j = 9为止,做法是完全相同的,最后输出的结果如下图,最终关键路径如图7-9-11所示。