ackerman函数
递归到非递归的转换
一. 为什么要转换
考虑函数的递归,因为第N次与第N+1次调用所采用的栈不能重用,可能会导致多次调用后,进程分配的栈空间耗尽.
解决的方法之一就是用自己可控制的栈代替函数调用栈,从而实现递归到非递归的转换.(用户栈当然必须是可以重用的,否则也就没有意义).
我们将会发现,实际上用户栈相比函数调用栈来说,可以非常小下面就以ackerman函数为例
二.ackerman函数
已知Ackerman函数akm(m,n)定义如下:
当m=0时: akm(m,n) = n + 1;
当m!=0, n=0时: akm(m,n) = akm(m-1, 1);
当m!=0, n!=0时: akm(m,n) = akm(m-1, akm(m, n-1));
(1) 根据定义,写出它的递归求解算法;
(2) 利用栈,写出它的非递归求解算法。
【解答】
(1) 已知函数本身是递归定义的,所以可以用递归算法来解决:
unsigned akm ( unsigned m, unsigned n ) {
if ( m == 0 ) return n+1; // m == 0
else if ( n == 0 ) return akm ( m-1, 1 ); // m > 0, n == 0
else return akm ( m-1, akm ( m, n-1 ) ); // m > 0, n > 0
}
(2) 为了将递归算法改成非递归算法.
首先改写原来的递归算法,将递归语句从结构中独立出来:
unsigned akm ( unsigned m, unsigned n ) {
unsigned v;
if ( m == 0 ) return n+1; // m == 0
if ( n == 0 ) return akm ( m-1, 1 ); // m > 0, n ==0
v = akm ( m, n-1 ) ); // m > 0, n > 0
return akm ( m-1, v );
}
然后,就是递归转非递归的标准流程:
a. 从一个简单的实例,分析其递归调用树
b. 分析哪些元素需要放在栈中
c. 跟踪递归调用过程,分析栈的变化
d. 由实例->普遍,演绎出算法,这一过程也称作建模
我们将会发现,建模是最困难的.
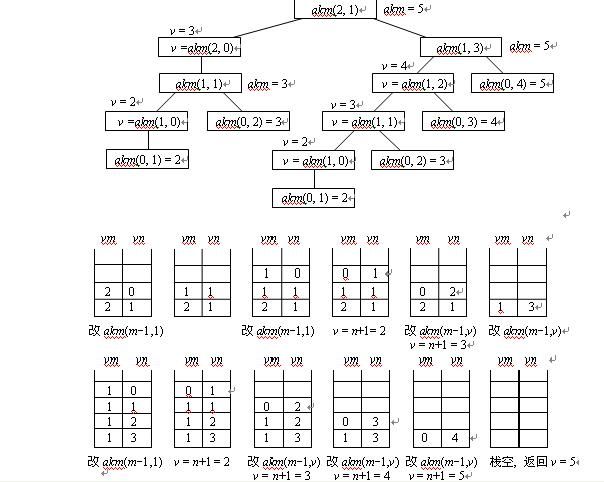
下面,我们就以ack(2,1)为例,开始分析递归调用树,采用一个栈记忆每次递归调用时的实参值,每个结点两个域{vm, vn}。对以上实例,递归树以及栈的变化如下:
相应算法如下
#include
#include
using namespace std;
typedef struct node_t {
unsigned int vm, vn;
}node, *pnode;
unsigned akm ( unsigned int m, unsigned int n ) {
std::stack st;
pnode w, w1;
unsigned int v;
unsigned int vt;
//根节点进栈
w = (node *) malloc (sizeof (node));
w->vm = m;
w->vn = n;
st.push (w);
do {
//计算akm(m-1, akm(m, n-1))
while ( st.top( )->vm > 0 ) {
vt = w->vn;
//计算akm(m, n-1), 直到akm(m,0)
while ( st.top()->vn > 0 )
{
w1 = (node *) malloc (sizeof (node));
vt --;
w1->vn = vt;
w1->vm = w->vm;
st.push( w1 );
}
//把akm(m, 0)转换为akm(m-1, 1),并计算
w = st.top( );
st.pop( );
w->vm--;
w->vn = 1;
st.push( w );
vt = w->vn;
}
//计算akm( 0, akm( 1, * ) )
w = st.top();
st.pop( );
w->vn++;
//计算v = akm( 1, * )+1
v = w->vn;
//如果栈不为空,改栈顶为( m-1, v )
if ( !st.empty( ) )
{
w = st.top();
st.pop( );
w->vm--;
w->vn = v;
st.push( w );
}
} while ( !st.empty( ) );
return v;
}
int main()
{
unsigned int rtn;
rtn = akm(3,2);
std::cout << rtn << std::endl;
return 0;
}
三.小结
主要难点在于最后的建模,怎样从一个或者几个实例,演绎出普适的数学模型,这是我做不到的,只有试图去理解,我想,勤能补拙只不过是一种安慰,真正创造性的工作,的确是聪明人的专利.另外一点感触就是,栈的应用可真是灵活啊!
在网上看到了一些人在找这个Ackerman函数 ,
不知道这个函数的实际含义,首先看到了他的递归形式:
注释部分是分析后的结果.
int rackerman(int m,int n)
{
if(m==0) return n+1; //更新n值,
else
if(n==0) return rackerman(m-1,1); //分析后要入栈一次, 同时n更新为 1
else
return rackerman(m-1,rackerman(m,n-1));//要先入m-1,然后入m. 同时 n-1
}
于是我在纸上模拟了几次栈的进出,发现只用m值在栈中进进出出,而n值是不断更新的,最后返回的值也是n值的变化.
.下面是我的非递归函数:
int
myAckerman(int m , int n )
{
list<int > listM;
listM.push_back(m);
while(! listM.empty() )
{
m=listM.back();
listM.pop_back();
if ( ! m )
{
n=n+1;
}
else if ( ! n )
{
m=m-1;
n=1;
listM.push_back(m);
}
else
{
n=n-1;
listM.push_back(m-1);
listM.push_back(m);
}
}
return n;
}
递归方法最简单,不需要说明。
#include "stdafx.h"
#include <iostream>
#include "time.h"
using std::cout;
using std::endl;
unsigned int akm(unsigned int m , unsigned int n)
...{
if(m==0) return n+1;
else if( n==0 ) return akm(m-1,1);
else return akm(m-1, akm(m,n-1));
}
int main(int argc, char* argv[])
...{
time_t x, y;
x = time(0);
cout<<"akm(1, 0) = "<<akm(1,0)<<endl;
y = time(0);
cout <<"using time is " << difftime(y, x) <<endl;
return 0;
}用for循环:
注意,申请的内存空间要足够大,反正我的计算机已经提出警告了,只能申请256M的内存。为什么要申请这么大的空间呢?由于ackerman是嵌套函数,他的值随时用来作为另外一个 函数的下标。因此,要申请足够的空间。不要以为只需要求ackerman(m, n)就for循环到m, n为止,这是错误的。
#include "stdafx.h"
#include <iostream>
using std::cout;
using std::endl;
const int maxN = 8500;
static int akm[maxN][maxN] =...{0};
int Ackerman(int m, int n)
...{
for(int j = 0; j <maxN; j++)
akm[0][j] = j+1;
for(int i = 1; i <maxN; i++)
...{
akm[i][0] = akm[i-1][1];
for(j = 1; j <= maxN; j++)
...{
akm[i][j] = akm[i-1][akm[i][j-1]];
}
}
return akm[m][n];
}
int main(int argc, char* argv[])
...{
cout<<"akm["<<3<<"]"<<"["<<9<<"]"<<" = "<<Ackerman(3, 9)<<endl;
cout<<"akm["<<3<<"]"<<"["<<10<<"]"<<" = "<<Ackerman(3, 10)<<endl;
return 0;
}
/
。
//以下方法被称为“备忘”。
可以,参看《算法导论》这本书的线性规划的后面部分。
同时必须指出:仍然申请的空间要足够的大,原因同上。否则要出错。
这个最多能算到ackerman(3,10) .内存大的应该还可以计算更大的。此种方法较为简单。
#include "stdafx.h"
#include <iostream>
#include "time.h"
const int maxN = 8500;
using std::cout;
using std::endl;
static int Ack[maxN][maxN];
void inint(void )
...{
for(int i = 0; i <maxN; i++)
for(int j = 0; j <maxN; j++)
Ack[i][j] = 0;
}
int Ackerman(int m, int n)
...{
int t = 0;
if(Ack[m][n] != 0)
return Ack[m][n];
if( m ==0 )
return n+1;
if ( n==0 )
t = Ackerman(m-1, 1);
if(m >=1 && n >= 1)...{
Ack[m][n-1] = Ackerman(m, n-1);
t = Ackerman(m-1, Ack[m][n-1]);
}
return (Ack[m][n] = t);
}
int main(int argc, char* argv[])
...{
time_t start, end;
inint();
start = time(0);
for(int i = 0 ; i <= 3; i++)
for(int j = 0; j <= 10; j++)
cout<<"Ack["<<i<<"]"<<"["<<j<<"]"<<" = "<<Ackerman(i, j)<<endl;
end = time(0);
cout<<"using time is "<<difftime(end, start)<<endl;
return 0;
}
不过在C语言中,一个函数是不能作为函数的形参进行传输的,只有特定的变量才能进行函数形参的传递.
这个函数用递归写成这样是错的吧??
#include<stdio.h>
int ack(int m,int n)
{
if(m==0) return (n+1);
else if(n==0) return ack(m-1,1);
else return ack(m-1,ack(m,n-1));
}
{
int m,n;
printf("input m n:/n");
scanf("%d %d",&m,&n);
printf("ack(%d,%d)=%d/n",m,n,ack(m,n));
getch();
}
#define MAX 30
/*范围定为30,可改大点*/
int Ackerman(int m,int n)
{
int i,j;
int t;
int a[MAX][MAX];/*存放结果*/
for(j=0;j<20;j++)
a[i][j]=0; /*数组初始化*/
a[0][j]=j+1; /* A(m,n)=n+1, 若 m=0*/
{
for(i=0;i<MAX;i++)
if(a[i-1][1]!= 0)
a[i][0]=a[i-1][1]; /* A(m,n)=[A(m-1,1), 若n=0 */
for(j=1;j<20;j++)
{
if((a[i][j-1] != 0)&&(a[i][j]==0) )
{
t=a[i][j-1];
if((a[i-1][t] != 0))
a[i][j]=a[i-1][t]; /* A(m-1,A(m,n-1)), 其他 */
}
}
}
return a[m][n];
}
{
int m,n;
printf("input m n:/n");
scanf("%d %d",&m,&n);
printf("ack(m,n)=%d/n",Ackerman(m,n));
return 0;
}
理论上一定会有结果,时间复杂度在MAX的四次方内.
但是实际上当m n稍微大点就会需要大于30的数组才能计算,尤其是m不能大(3以内).
否则很容易陷入死循环,
因为定义的数组不够大,硬件和时间限制,呵呵