计算数字滤波器的频率响应

计算数字滤波器的频率响应

今天在一本书上看到了个计算数字滤波器频响的代码，这个代码还算有用，就整理了一下。代码写的挺长的，下面是原始的代码。

/**
 * 计算数字滤波器的频率响应
 * num 是数字滤波器的分子多项式系数
 * den 是数字滤波器的分母多项式系数
 * num_order 是分子多项式的阶数
 * den_order 是分母多项式的阶数
 * sign = 0 时，x_out 为频率响应的实部， y_out 为频率响应的虚部
 * sign = 1 时，x_out 为频率响应的模， y_out 为频率响应的幅角
 * sign = 2 时，x_out 为以 dB 为单位的频率响应， y_out 为频率响应的幅角
 * len 为，频率响应的取样点数
 */
void gain(double num[], double den[], int num_order, int den_order,
          double x_out[], double y_out[], int len, int sign)
{
    int i, k;
    double zr, zi;
    double re, im;
    double ar, ai, br, bi;
    double numr, numi;
    double de, temp;
    double freq;
    for(k = 0; k < len; k++)
    {
        freq = 0.5 * k / (len - 1);
        zr = cos(-2.0 * M_PI * freq);
        zi = sin(-2.0 * M_PI * freq);
        br = 0.0;
        bi = 0.0;
        for(i = num_order; i > 0; i--)
        {
            re = br;
            im = bi;
            br = (re + num[i]) * zr - im * zi;
            bi = (re + num[i]) * zi + im * zr;
        }
        ar = 0.0;
        ai = 0.0;
        for(i = den_order; i > 0; i--)
        {
            re = ar;
            im = ai;
            ar = (re + den[i]) * zr - im * zi;
            ai = (re + den[i]) * zi + im * zr;
        }
        br = br + num[0];
        ar = ar + 1.0;
        numr = ar * br + ai * bi;
        numi = ar * bi - ai * br;
        de = ar * ar + ai * ai;
        x_out[k] = numr / de;
        y_out[k] = numi / de;
        switch(sign)
        {
        case 1:
            temp = hypot(x_out[k], y_out[k]);
            y_out[k] = atan2(y_out[k], x_out[k]);
            x_out[k] = temp;
            break;
        case 2:
            temp = x_out[k] * x_out[k] + y_out[k] * y_out[k];
            y_out[k] = atan2(y_out[k], x_out[k]);
            x_out[k] = 10 *log10(temp);
            break;
        default:
            break;
        }
    }
}

下面是个测试例子，滤波器系数如下：

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
void gain(double num[], double den[], int num_order, int den_order,
          double x_out[], double y_out[], int len, int sign);

#define N 200
int main()
{
    double den[] = {1.0, 0.0, 0.9};
    double num[] = {0.0, -1.0};
    double x_out[N], y_out[N];
    int i;
    double f;
    gain(num, den, 1, 2, x_out, y_out, N, 1);
    for(i = 0; i < N; i ++)
    {
        f = 0.5 * i / (N - 1);
        printf("%f, %f, %f\n", f, x_out[i], y_out[i]);
    }
    return 0;
}

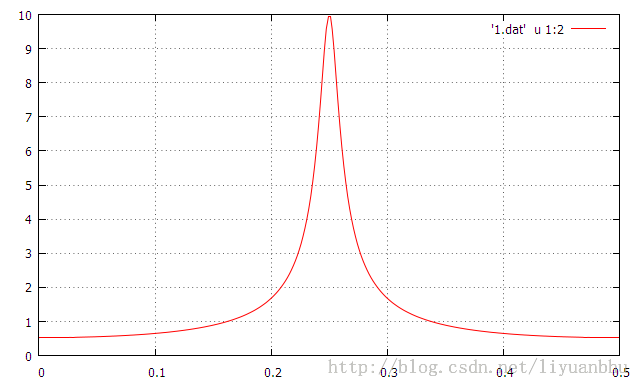
下面是计算出的幅频特性曲线。

下面是计算出的相频特性曲线。

上面的代码虽然计算结果看起来没什么问题，不过这么简单的功能写了这么多行也有点啰嗦。下面是我给出的另外几种实现方法。

数字滤波器的传递函数可以写为：

其中a[0] 通常为 1。

频率响应为：

其中

可以看出传递函数其实就是两个多项式的结果相除。所以如果能写出个多项式求值的代码，自然也就能写出频率特性计算的代码了。

因此先写个多项式求值的代码，用到了些C99的特性（对复数运算的支持）

double _Complex poly_val(double p[], int n, double omega)
{
    int i;
    double _Complex z, sum = 0;
    for (i = 0; i < n; i++)
    {
        z = cos(i * omega) - I * sin(i * omega);
        sum += p[i] * z;
    }
    return sum;
}

有了这个代码，后面的代码就很容易写出来了。

void gain(double num[], double den[], int num_size, int den_size, double _Complex out[], int n)
{
    double omega;
    int i;
    for (i = 0; i < n; i++)
    {
        omega = M_PI * i / (n-1);
        out[i] = poly_val(num, num_size, omega) / poly_val(den, den_size, omega);
    }
}

下面是测试代码，可以验证计算结果是相同的。

#define N 200
int main()
{
    double den[] = {1.0, 0.0, 0.9};
    double num[] = {0.0, -1.0};
    double _Complex out[N];
    int i;
    double f;
    gain(num, den, 2, 3, out, N);

    for(i = 0; i < N; i ++)
    {
        f = 0.5 * i / (N - 1);
        printf("%f, %f, %f\n", f, cabs(out[i]), carg(out[i]));
    }
    return 0;
}

这个代码与原来的代码最大的区别就是调用 sin 和 cos 的次数多一些。之所以代码调用 sin 和 cos次数少，是因为用到了多项式计算的Horner 方法。

我专门有一篇文章介绍 多项式计算的Horner 方法，所以这里就不多说了。下面给个利用Horner 的代码，实现的功能与书上的代码的功能完全相同。

double _Complex poly_val2(double p[], int order, double omega)
{
    int i;
    double _Complex z, sum = 0;

    sum = 0.0;
    z = cos(omega) - I * sin(omega);
    for (i = order; i >= 0; i--)
    {
        sum = sum * z + p[i];
    }
    return sum;
}

/**
 * 计算数字滤波器的频率响应
 * num 是数字滤波器的分子多项式系数
 * den 是数字滤波器的分母多项式系数
 * num_order 是分子多项式的阶数
 * den_order 是分母多项式的阶数
 * sign = 0 时，x_out 为频率响应的实部， y_out 为频率响应的虚部
 * sign = 1 时，x_out 为频率响应的模， y_out 为频率响应的幅角
 * sign = 2 时，x_out 为以 dB 为单位的频率响应， y_out 为频率响应的幅角
 * len 为，频率响应的取样点数
 */
void gain2 (double num[], double den[], int num_order, int den_order,
            double x_out[], double y_out[], int len, int sign)
{
    int k;
    double omega;
    double _Complex h;
    for (k = 0; k < len; k++)
    {
        omega = M_PI * k / (len-1);
        h = poly_val2(num, num_order, omega) / poly_val2(den, den_order, omega);
        switch(sign)
        {
        case 1:
            y_out[k] = carg(h);
            x_out[k] = cabs(h);
            break;
        case 2:
            y_out[k] = carg(h);
            x_out[k] = 20 * log10(cabs(h));
            break;
        default:
            x_out[k] = creal(h);
            y_out[k] = cimag(h);
            break;
        }
    }
}

#define N 200
int main( void )
{
    double den[] = {1.0, 0.0, 0.9};
    double num[] = {0.0, -1.0};
    int i;
    double f;
    double x_out[N], y_out[N];
    gain2(num, den, 1, 2, x_out, y_out, N, 1);

    for(i = 0; i < N; i ++)
    {
        f = 0.5 * i / (N - 1);
        printf("%f, %f, %f\n", f, x_out[i], y_out[i]);
    }
    return 0;
}