最小生成树之kruskal算法

kruskal算法的精髓在于：

每次选取一条边。

该边同时满足：1、在当前未选边中权值最小；2、与已选边不构成回路。

直到选取n-1条表是算法结束。找到MST活判断不存在MST。

 

代码设计：

1、利用优先级队列将权值小的边放到队列最前，优先出对，保证了每次选择的都是权值最小的边。

2、利用并查集的查找及结合把同处同一连通分量中的顶点连到同一父节点下。这样，每次判断是

否构成回路，只要判断父节点是否相同的即可。

 

代码：

#include<iostream>
#include<cmath>
#include<queue>
using namespace std;

const int maxn=101;  //图的最大节点数 

struct edge  //边 
{
    int from;  //起点 
    int to;    //终点 
    int cost;  //路径长 
    
    friend bool operator < (const edge &e1,const edge &e2)
    {
        return e1.cost>e2.cost;
    }
};

edge remMST[maxn];   //记录组成最小生成树的边  
int father[maxn];    //用来做并查集 
int nodeNum,edgeNum;  //顶点数、边数 
int MST;                //最小生成树 
priority_queue<edge> myQ;   //kruskal算法，存放边 

void storeMap()   //存储岛的桥构成的图 
{
    while(!myQ.empty()) myQ.pop();  //清空 
    
    int  from,to,cost;
    for(int i=0;i<edgeNum;i++)    //kruskal算法对于无向图也只需建一条边即可 
    {
        scanf("%d%d%d",&from,&to,&cost);

        edge e;
        e.from=from;
        e.to=to;
        e.cost=cost;
            
        myQ.push(e);
    }
}   
 
int find(int x)  //查找 
{
    if(x==father[x]) return father[x];
    return father[x]=find(father[x]);
}

bool judge()   //判断是否是一棵最小生成树 ,这里得注意起点和终点 
{
    int f=find(1);
    
    for(int i=2;i<=nodeNum;i++)
    {
        if(f!=find(i))
        {
            return false;
        }
    }
    
    return true;
}

void kruskal()   //kruskal算法 
{
    MST=0;
    
    for(int i=0;i<maxn;i++)
    {
        father[i]=i;
    }
    
    int num=0;   //记录MST的边数 
    while(!myQ.empty() && num!=nodeNum-1)
    {
        edge e=myQ.top();
        myQ.pop();
        
        int fx=find(e.from);
        int fy=find(e.to);
        
        if(fx!=fy)
        {
            father[fx]=fy;
            MST+=e.cost;
            
            remMST[num].from=e.from;
            remMST[num].to=e.to;
            remMST[num].cost=e.cost;
             
            num++;
        }
    }
}       

void output()   //打印最小生成树的值以及由哪些边组成 
{
    if(judge())
    {
        printf("from <-> to  cost:\n"); 
        for(int i=0;i<nodeNum-1;i++)
        {
            printf("%d %d %d\n",remMST[i].from,remMST[i].to,remMST[i].cost);
        } 
        printf("MST Is : %d\n",MST);
    } 
    else printf("No MST Exist!\n"); 
}
                  
int main()
{
    while(scanf("%d%d",&nodeNum,&edgeNum)!=EOF) 
    {
        storeMap();
         
        kruskal();
        
        output(); 
    }
    
    system("pause");
    return 0;
}        

 

测试实例：

1、图形

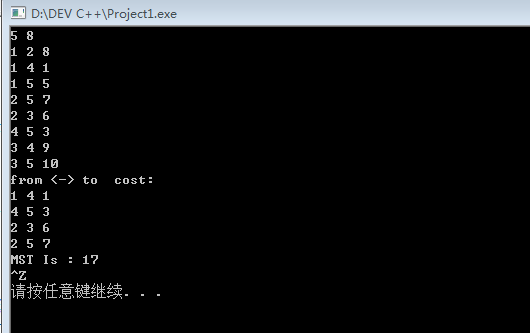
2、输入及结果

 

问题：

还是如何利用kruskal算法求解有向图的MST？

也留着吧。。。