文本建模常用的预处理方法——特征选择方法(CHI和IG)
本篇关于TF-IDF/CHI/IG。
参考:
http://blog.sina.com.cn/s/blog_6622f5c30101datu.html
http://lovejuan1314.iteye.com/blog/651460
1)TF-IDF在特征选择时的误区。
TF-IDF用于向量空间模型,进行文档相似度计算是相当有效的。但在文本分类中单纯使用TF-IDF来判断一个特征是否有区分度是不够的。
===》它仅仅综合考虑了该词在文档中的重要程度和文档区分度。
===》它没有考虑特征词在类间的分布。特征选择所选择的特征应该在某类出现多,而其它类出现少,即考察各类的文档频率的差异。如果一个特征词,在各个类间分布比较均匀,这样的词对分类基本没有贡献;但是如果一个特征词比较集中的分布在某个类中,而在其它类中几乎不出现,这样的词却能够很好代表这个类的特征,而TF-IDF不能区分这两种情况。
===》它没有考虑特征词在类内部文档中的分布情况。在类内部的文档中,如果特征词均匀分布在其中,则这个特征词能够很好的代表这个类的特征,如果只在几篇文档中出现,而在此类的其它文档中不出现,显然这样的特征词不能够代表这个类的特征。
2)特征选择方法综述。
文本中能观察到的量其实只有两个:词频和文档频率,所有的方法一律以这两个量为计算基础。
针对英文纯文本的实验结果表明:作为特征选择方法时,卡方检验和信息增益的效果最佳(相同的分类算法,使用不同的特征选择算法来得到比较结果);文档频率方法(直接依据文档频率大小排序的方法)的性能同前两者大体相当,术语强度方法性能一般;互信息方法的性能最差。
3)信息增益。
在文本分类中,特征词t的取值只有t(代表t出现)和![]() (代表t不出现)。那么
(代表t不出现)。那么
![]()
最后,信息增益
但信息增益最大的问题还在于它只能考察特征对整个系统的贡献,而不能具体到某个类别上,这就使得它只适合用来做所谓“全局”的特征选择(指所有的类都使用相同的特征集合),而无法做“本地”的特征选择(每个类别有自己的特征集合,因为有的词,对这个类别很有区分度,对另一个类别则无足轻重)。
实现方法:
1 统计正负分类的文档数:N1、N2。
2 统计每个词的正文档出现频率(A)、负文档出现频率(B)、正文档不出现频率(C)、负文档不出现频率(D)。
3 计算信息熵
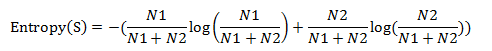
4 计算每个词的信息增益

5 将每个词按信息增益值从大到小排序,选取前k个词作为特征,k即特征维数。
4)卡方检测,CHI-Square test。
卡方检验最基本的思想就是通过观察实际值与理论值的偏差来确定理论的正确与否。具体做的时候常常先假设两个变量确实是独立的(“原假设”),然后观察实际值(观察值)与理论值(这个理论值是指“如果两者确实独立”的情况下应该有的值)的偏差程度,如果偏差足够小,我们就认为误差是很自然的样本误差,是测量手段不够精确导致或者偶然发生的,两者确确实实是独立的,此时就接受原假设;如果偏差大到一定程度,使得这样的误差不太可能是偶然产生或者测量不精确所致,我们就认为两者实际上是相关的,即否定原假设,而接受备择假设。
理论值为E,实际值为x,偏差程度的计算公式为:
这个式子就是开方检验使用的差值衡量公式。当提供了数个样本的观察值x1,x2,……xi,……xn之后,代入到式中就可以求得卡方值,用这个值与事先设定的阈值比较,如果大于阈值(即偏差很大),就认为原假设不成立,反之则认为原假设成立。
在文本分类的特征选择阶段,一般使用“词t与类别c不相关”来做原假设,计算出的开方值越大,说明对原假设的偏离越大,我们越倾向于认为原假设的反面情况是正确的。选择的过程为每个词计算它与类别c的开方值,从大到小排个序(此时开方值越大越相关),取前k个就可以。
卡方检验的缺点是:它只统计文档是否出现词,而不管出现了几次。这会使得他对低频词有所偏袒(因为它夸大了低频词的作用)。甚至会出现有些情况,一个词在一类文章的每篇文档中都只出现了一次,其开方值却大过了在该类文章99%的文档中出现了10次的词,其实后面的词才是更具代表性的,但只因为它出现的文档数比前面的词少了“1”,特征选择的时候就可能筛掉后面的词而保留了前者。这就是开方检验著名的“低频词缺陷”。因此开方检验也经常同其他因素如词频综合考虑来扬长避短。
实现方法:
1 统计样本集中文档总数(N)。
2 统计每个词的正文档出现频率(A)、负文档出现频率(B)、正文档不出现频率(C)、负文档不出现频率(D)。
3 计算每个词的卡方值,公式如下:
4 将每个词按卡方值从大到小排序,选取前k个词作为特征,k即特征维数。
文本建模系列会不断更新。。。。
