深入浅出游戏算法(2)-图形数学基础（1）

一、右手坐标系

直角坐标系的 x-轴，y-轴，与 z-轴必须相互垂直。称包含 z-轴的直线为 z-线。在三维空间里，当我们设定了 x-轴，y-轴的位置与方向的同时，我们也设定了 z-线的方向。可是，我们仍旧必须选择，在 z-线以原点为共同点的两条半线中，那一条半线的点的坐标是正值的，那一条是负值的？这两种不同的坐标系统，称为右手坐标系与左手坐标系。右手坐标系又称为标准坐标系，或正值坐标系。（左边为左手坐标系，右边为右手坐标系） 

右手坐标系这名词是由右手定则而来的。先将右手的手掌与手指伸直。然后，将中指指向往手掌的掌面 半空间，与食指呈直角关系。再将大拇指往上指去，与中指，食指都呈直角关系。则大拇指，食指，与中指分别表示了右手坐标系的 x-轴，y-轴，与 z-轴。同样地，用左手也可以表示出左手坐标系。

三维坐标系分类

1、世界坐标系

描述整个世界或整个场景的每件事物（包括人、动物等）的位置，作为三维坐标系，描述的方式是会标（x,y,z)，分别代表了事物在三维坐标系中X、Y、Z轴的坐标。

2、物体坐标系

每个物体内部的坐标体系，以度量物体组成部分之间的相对位置，物体如果发生移动，相对世界坐标系而言，物体坐标系也随之整体移动。

3、惯性坐标系统，与物体坐标系不同之处在于，它们的轴方向不同，但它们原点位置相同，这意味着，惯性坐标系通过旋转可与物体坐标系统重合，惯性坐标系通过平移可与世界坐标系统重合。

4、坐标转换：

  通过将物体坐标系先旋转成为惯性坐标系，然后再平移成为世界坐标系。

二、向量

   标量仅为单个数值，而向量可以由多个或单个数值（标量可以视为一维向量）组成，向量有大小和方向，大小即模长，方向即向量的指向，向量中数值的数量为向量的维度。一维向量可以表示为[v1]，而二维向量可表示为[v1,v2]，三维向量可表示为[v1,v2.v3]，n维向量可表示为[v1,v2,...,vn]。

向量的2个度量属性方向与长度决定了向量可以描述物体在空间中的运动，其长度是物体移动的距离，但不是位置，位置可描述坐标系中的一个点，位置通常用(x,y,z)这种用圆括号包围的方式表示。其方向是运动的方向。比如：[3,-2,9]表示，物体向X正轴方向移动3个单位，向Y负轴方向移动2个单位，向Z正轴方向移动9个单位，可以同时移动，也可以依次移动。

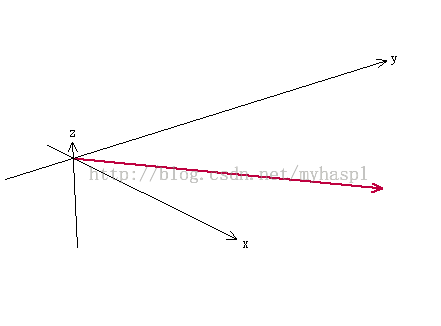
下图描述了向量[5,9,-2]，它从(0,0,0)出发到(5,9,-2)，图中向量表现为具有一定长度、指定方向（用箭头表示）的直线，它在X轴和Y轴上均为正方向，而在Z轴上为负方向。

麦好的AI乐园博客所有内容是原创，如果转载请注明来源

http://blog.csdn.net/myhaspl/

对于n维向量V[v1,v2,...,vn]，其模长计算公式为：

上图中的所示向量的长度为：