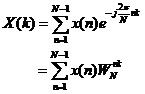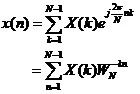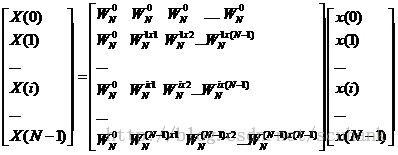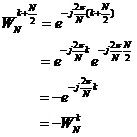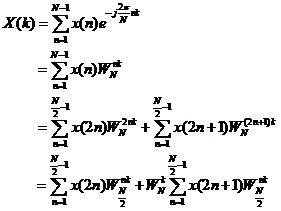快速傅里叶变换及其实现
一、基本原理
长度为N的有限长离散序列的傅里叶变换的定义为:
(1)
逆变换:
(2)
用矩阵来表达傅里叶变换为:
(4)
逆变换:
(5)
(6)
因此,
(7)
二、N点FFT分解运算
对序列进行N点FFT的分解运算时,应注意以下问题:
第一,若序列为顺序输入,则输出序列为输入序列的比特位反序序列。
第二,将N点FFT的完整运算分为![]() 级,每级分为
级,每级分为![]() 个群组,每个群组分为
个群组,每个群组分为![]() 次蝶形运算。
次蝶形运算。
第三,每个群组中,第p次蝶形运算的上下分支序号相差![]() ,而上下分支系数分别为
,而上下分支系数分别为![]() 和
和![]() 。
。
第四,根据式(4)得知,N点FFT的系数![]() 仅需要个
仅需要个![]() 。因此,对每个蝶形运算的上下分支系数应先进行判断,即
。因此,对每个蝶形运算的上下分支系数应先进行判断,即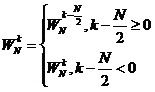 :
:
(8)
N点FFT的计算过程如下:
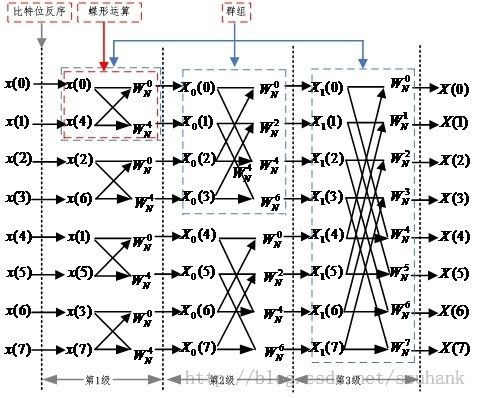
三、8点FFT计算流程图
图一
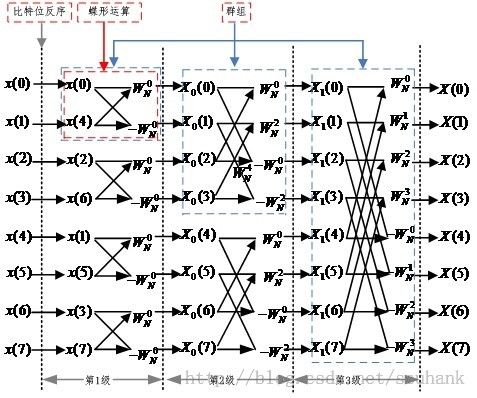
图二
四、N点FFT的程序实现
根据FFT的基本原理及前面的图解,按照FFT流程从程序上实现快速傅里叶变换及其反变换(假定),附代码如下(Linux、Windows下可准确运行):
#include <stdio.h>
#include <math.h>
#include <complex>
const double PI = 3.1415926;
void display(std::complex<double>* pclsMat, int n)
{
if(NULL == pclsMat || n < 0)
{
return;
}
for(int i = 0; i < n; i++)
{
double re = pclsMat[i].real(),
im = pclsMat[i].imag();
char ch = im>=0?'+':'-';
im = fabs(im);
printf("pclsMat[%d] = %.5f %c j*%.5f\n", i,re,ch,im);
}
}
/*
* 计算基于2底n的对数
*/
int log2(int n)
{
int i = 0;
while((1<<i)<n)
{
i++;
}
return i;
}
/*
*将大小为n的复数数组pclsMat2复制到pclsMat1
*/
bool arrcpy(std::complex<double>* pclsMat1, std::complex<double>* pclsMat2, int n)
{
if(NULL == pclsMat1 || NULL == pclsMat2 || n < 1)
{
return false;
}
while(n)
{
*pclsMat1++ = *pclsMat2++;
n--;
}
return true;
}
/*
* 计算in按比特位反序的值,比特位数为n的二进制的比特位数
* */
int invid(int in,intn)
{
if(in>=n || n < 1 || in < 0)
{
return -1;
}
int out = 0,
i = 0;
i = log2(n);
while(i)
{
out += (in%2)*(1<<(i-1));
i--;
in /= 2;
}
return out;
}
/*
* 将大小为n的复数数组pclsMat1复制到数组下标为pclsMat1数组下标比特位反序数组 * 中
* */
bool invmat(std::complex<double>* pclsMat1, std::complex<double>* pclsMat2, int n)
{
if(NULL == pclsMat1 || NULL == pclsMat2 || n < 1)
{
return false;
}
for(int i = 0; i < n; i++)
{
int j = invid(i,n);
pclsMat2[j] = pclsMat1[i];
//printf("pclsMat2[%d]-> pclsMat1[%d]\n",j,i);
}
return true;
}
/*
* 计算WN值
* style:
* 0-fft
* 1-ifft
* */
bool comw(std::complex<double>* pclsW,int n, int style)
{
if(NULL == pclsW || n < 1)
{
return false;
}
for(int i = 0; i < n; i++)
{
double angle;
if(0 == style)
angle = -PI*i/n;
else if(1 == style)
angle = PI*i/n;
std::complex<double> wi = std::complex<double>(cos(angle), sin(angle));
pclsW[i] = wi;
}
return true;
}
/*
* 计算时域序列/频域序列pclsMat1的n点DFT/IDFT到频域序列/时域序列pclsMat2中
* style:
* 0:fft
* 1:ifft
*/
bool fft(std::complex<double>* pclsMat1, std::complex<double>* pclsMat2,int n, int style)
{
if(NULL == pclsMat1 || NULL == pclsMat2 || n < 1)
{
return false;
}
invmat(pclsMat1,pclsMat2,n);//对输入的时域序列进行bit位反转
arrcpy(pclsMat1, pclsMat2,n);
intn2 = n/2;
std::complex<double>* pclsW = new std::complex<double>[n2];
comw(pclsW,n2, style); //计算WNr系数,只需要序列总数的一半
int m = log2(n);
for(int i = 0; i < m; i++)//级数m=log2(n)
{
int r = 1<<(m-1-i); //群组个数
//蝶形运算的下分支与上分支的序号差值或者每个群组中的蝶形运算次数
int s = 1<<i;
//一次群组所有蝶形运算结束后下一群组计算时数组的起始下标值
int c = 1<<(i+1);
int k = 0;
for(int j = 0; j < r; j++) //循环的群组次数
{
for(int p = 0; p < s; p++) //每个群组中的蝶形运算次数
{
//计算蝶形运算上下分支的系数WNr
int wnUp = p * r;
int wnDn = (p + s) * r;
//根据WNr的对称性计算WNr(k+N/2)=-WNr(k)
std::complex<double>wnUpCx=(wnUp-n2)>= 0? wnUp-=n2,-pclsW[wnUp] : pclsW[wnUp];
std::complex<double>wnDnCx=(wnDn-n2)>=0? wnDn-=n2,-pclsW[wnDn] : pclsW[wnDn] ;
//计算蝶形运算上下分支的结果值
pclsMat2[k+p] = pclsMat1[k+p] + pclsMat2[k+p+s] * wnUpCx;
pclsMat2[k+p+s] = pclsMat1[k+p] + pclsMat2[k+p+s] * wnDnCx;
//printf("pclsMat2[%d]= pclsMat1[%d]+pclsMat1[%d]*WNr[%d] \n",k+p,k+p,k+p+s,wnUp);
//printf("pclsMat2[%d] = pclsMat1[%d]-pclsMat1[%d]*WNr[%d]\n",k+p+s,k+p,k+p+s,wnDn);
//printf("pclsMat2[%d] = [%.5f + j*%.5f]+[%.5f + j*%.5f]*[%.5f + j*%.5f] = [%.5f + j*%.5f]\n",k+p,pclsMat1[k+p].real(),pclsMat1[k+p].imag(),pclsMat1[k+p+s].real(),pclsMat1[k+p+s].imag(),wnUpCx.real(),wnUpCx.imag(), pclsMat2[k+p].real(),pclsMat2[k+p].imag());
//printf("pclsMat2[%d] = [%.5f + j*%.5f]+[%.5f + j*%.5f]*[%.5f + j*%.5f] = [%.5f + j*%.5f]\n",k+p+s,pclsMat1[k+p].real(),pclsMat1[k+p].imag(),pclsMat1[k+p+s].real(),pclsMat1[k+p+s].imag(),wnDnCx.real(),wnDnCx.imag()),pclsMat2[k+p+s].real(),pclsMat2[k+p+s].imag();
}
k += c;
}
//printf("===============%d-th transfrom ===================\n",i);
arrcpy(pclsMat1, pclsMat2, n);
//display(pclsMat2,n);
//printf("\n");
}
//计算ifft
if(1 == style)
{
for(int i = 0; i < n; i++)
{
pclsMat2[i] /= n;
}
}
delete []pclsW;
return true;
}
int main()
{
int n = 32;
std::complex<double>* pclsMat1 =new std::complex<double>[n];
std::complex<double>* pclsMat2 =new std::complex<double>[n];
/*pclsMat1[0] = 1;
pclsMat1[1] = 2;
pclsMat1[2] = -1;
pclsMat1[3] = 3;*/
for(int i = 0; i < n; i++)
{
pclsMat1[i] = std::complex<double>(i,i);
}
printf("===================source sequence=======================\n");
display(pclsMat1, n);
fft(pclsMat1, pclsMat2, n,0);
printf("===================fft translate=========================\n");
display(pclsMat2, n);
fft(pclsMat2, pclsMat1, n,1);
printf("==================ifft translate=========================\n");
display(pclsMat1, n);
delete []pclsMat1;
delete []pclsMat2;
return 0;
}
[参考文献]:
[1]. 郑君里等.信号与系统(第二版)下册.北京:高等教育出版社
[2]. 奥本海姆著,刘树棠译.离散时间信号处理(第二版).西安:西安交通大学出版社
[3]. 冈萨雷斯著,阮秋琦译.数字图像处理(第三版).北京:电子工业出版社