插头DP——从不会到入门(POJ 2411,HDU 1565,HDU 2167,HDU 1693,Ural 1519)
最近两周一直在刷DP题,前几天接触了插头DP。说实话,直接做“入门”题Ural 1519 Formula 1难度略大,而网上也没有个由浅入深的题表和教程。故总结了一下最近做的、适合作为插头DP专题入门题的题目,专心写一篇博客。大牛见笑。
学习插头DP前,你得搞清楚状态压缩DP是什么。这里推荐AcCry的一篇状态压缩教程:状态压缩总结。刷完教程里的8题之后,状态压缩DP也就是入门了,也就可以开始学习插头DP了。
POJ 2411 Mondriaan's Dream
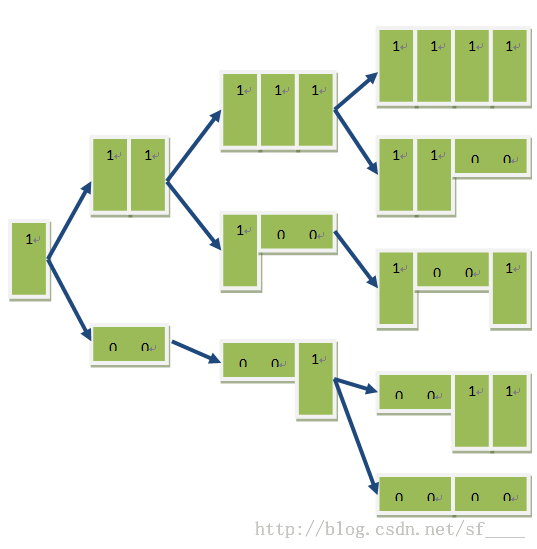
1*2砖填充矩形,问多少种方法。这道题一般想到的方法都是状态压缩DP,上面AcCry的教程中也有这题。但是有更快的方法(不是打表= =),我们可以不按照一行一行匹配、转移的做法,而是一格一格直接转移。这是我第一次接触插头DP,在这篇解题报告上看到的:http://blog.csdn.net/fp_hzq/article/details/6427072。他写的代码很短,POJ上16MS搞定,让我顿时来了兴趣。不过他的代码真的不好理解。研究了很久,画个图给大家看吧。我们可以用1表示该处竖着放一块砖,用0表示横着放的砖,或者竖着放的第二行。或者这样说,1表示下一行此处不可以放砖,0表示下一行此处可以放砖。状态的转移有两种。见下图。
然后,代码如下:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
long long dp[2][1<<11];
int main()
{
int n,m;
while(scanf("%d%d",&n,&m),(n||m))
{
int total=1<<m;
int pre=0,now=1;
memset(dp[now],0,sizeof(dp[now]));
dp[now][0]=1;
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
{
swap(now,pre);
memset(dp[now],0,sizeof(dp[now]));
for(int S=0;S<total;S++) if( dp[pre][S] )
{
dp[now][S^(1<<j)]+=dp[pre][S];
if( j && S&(1<<(j-1)) && !(S&(1<<j)) )
dp[now][S^(1<<(j-1))]+=dp[pre][S];
}
}
printf("%lld\n",dp[now][0]);
}
} 这是初学的时候写的代码,下面给出模板化的代码:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define LL long long
const int maxn=2053;
struct Node
{
int H[maxn];
int S[maxn];
LL N[maxn];
int size;
void init()
{
size=0;
memset(H,-1,sizeof(H));
}
void push(int SS,LL num)
{
int s=SS%maxn;
while( ~H[s] && S[H[s]]!=SS )
s=(s+1)%maxn;
if(~H[s])
{
N[H[s]]+=num;
}
else
{
S[size]=SS;
N[size]=num;
H[s]=size++;
}
}
LL get(int SS)
{
int s=SS%maxn;
while( ~H[s] && S[H[s]]!=SS )
s=(s+1)%maxn;
if(~H[s])
{
return N[H[s]];
}
else
{
return 0;
}
}
} dp[2];
int now,pre;
int get(int S,int p,int l=1)
{
if(p<0) return 0;
return (S>>(p*l))&((1<<l)-1);
}
void set(int &S,int p,int v,int l=1)
{
S^=get(S,p,l)<<(p*l);
S^=(v&((1<<l)-1))<<(p*l);
}
int main()
{
int n,m;
while( scanf("%d%d",&n,&m),n||m )
{
if(n%2 && m%2) {puts("0");continue;}
int now=1,pre=0;
dp[now].init();
dp[now].push(0,1);
for(int i=0;i<n;i++) for(int j=0;j<m;j++)
{
swap(now,pre);
dp[now].init();
for(int s=0;s<dp[pre].size;s++)
{
int S=dp[pre].S[s];
LL num=dp[pre].N[s];
int p=get(S,j);
int q=get(S,j-1);
int nS=S;
set(nS,j,1-p);
dp[now].push(nS,num);
if(p==0 && q==1)
{
set(S,j-1,0);
dp[now].push(S,num);
}
}
}
printf("%lld\n",dp[now].get(0));
}
} 按照Kuangbin大神说的,自己慢慢形成自己的模板风格就好了。
这一题,主要学习逐格递推的方式。状态压缩DP是枚举两行的状态,找到匹配的状态后转移,复杂度为n*2^2n。而逐格转移省去了很多无用的状态,复杂度也小了很多,为n^2*2^n。
HDU 1565 方格取数(1)
依旧是状态压缩DP可以做的题目。取一个数字,周围四个数字不可取。做法类似于上题。取数字的位置标记为1,不取标记为0。转移时,我一定可以不取。如果当前行上一行没有取数字,左边的一格没有取数字,这一格我可以取。代码如下:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int dp[2][1<<20];
int main()
{
int n;
while(~scanf("%d",&n))
{
int total=1<<n;
int now=1,pre=0;
for(int S=0;S<total;S++)
dp[now][S]=-1;
dp[now][0]=0;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
{
swap(now,pre);
for(int S=0;S<total;S++)
dp[now][S]=-1;
int v;
scanf("%d",&v);
for(int S=0;S<total;S++) if(~dp[pre][S])
{
int not=S&(~(1<<j));
dp[now][not]=max(dp[now][not],dp[pre][S]);
if(!(S&(1<<j)) && ( j==0 || (j>0 && !(S&(1<<(j-1)))) ))
dp[now][S^(1<<j)]=max(dp[pre][S]+v,dp[now][S^(1<<j)]);
}
}
int ans=0;
for(int S=0;S<total;S++) if(~dp[now][S])
ans=max(ans,dp[now][S]);
printf("%d\n",ans);
}
} 模板化代码:
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
#define LL long long
const int maxn=10011;
struct Node
{
int H[maxn];
int S[maxn];
int N[maxn];
int size;
void init()
{
size=0;
memset(H,-1,sizeof(H));
}
void push(int SS,int num)
{
int s=SS%maxn;
while( ~H[s] && S[H[s]]!=SS )
{
s++;
s%=maxn;
}
if(~H[s])
{
N[H[s]]=max(N[H[s]],num);
return;
}
N[size]=num;
S[size]=SS;
H[s]=size++;
}
} dp[2];
int now,pre;
int get(int S,int p,int l=1)
{
return (S>>(p*l))&((1<<l)-1);
}
void set(int &S,int p,int v,int l=1)
{
S^=get(S,p,l)<<(p*l);
S^=(v&((1<<l)-1))<<(p*l);
}
int main()
{
int n;
while(~scanf("%d",&n))
{
now=1;
pre=0;
dp[now].init();
dp[now].push(0,0);
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
{
int v;
scanf("%d",&v);
swap(now,pre);
dp[now].init();
for(int s=0;s<dp[pre].size;s++)
{
int S=dp[pre].S[s];
int num=dp[pre].N[s];
if( get(S,j)==0
&& ( j==0 || get(S,j-1)==0 ) )
{
set(S,j,1);
dp[now].push(S,v+num);
}
set(S,j,0);
dp[now].push(S,num);
}
}
nth_element(dp[now].N,dp[now].N+dp[now].size-1,dp[now].N+dp[now].size);
printf("%d\n",dp[now].N[dp[now].size-1]);
}
}
HDU 2167 Pebbles
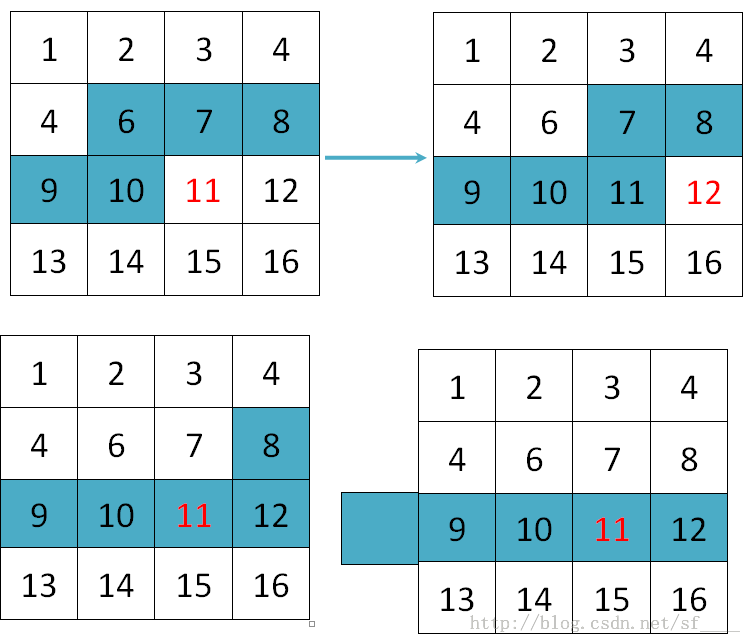
相对上一题方格取数,这一题要高级很多了。首先输入比较难处理,其次周围8格数字不可取,上一题的方法不能直接使用了。因为必须要记录当前格左上角的数字有没有取得情况,我们需要在状态中加一位,并且换行时要更新一下状态。如下图:在取11格的数字时,我们需要判断10,6,7,8格是否有取数字。在更新11格的状态的同时,丢弃掉第6格的状态值。在遇到换行时,第8格的状态可以直接丢弃,但是我们要虚拟出一个新的格,方便下一次的状态转移。这题要理解多加的状态,以及换行时的状态变化。此时的状态记录已经类似于下面说的轮廓线了。代码如下:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int dp[2][1<<16];
int main()
{
while(1)
{
int n=16;
int t=0;
int total=1<<n;
int now=1,pre=0;
for(int S=0;S<total;S++)
dp[now][S]=-1;
dp[now][0]=0;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
{
int v;
char ch;
if(scanf("%d%c",&v,&ch)==-1)
return 0;
t++;
if(ch=='\n' && n==16) n=t,total=1<<(n+1);
swap(now,pre);
for(int S=0;S<total;S++)
dp[now][S]=-1;
for(int S=0;S<total;S++) if(~dp[pre][S])
{
if(j==0)
{
int SS=(S<<1)&(~(1<<(n+1)));
dp[now][SS&(~1)]=max(dp[pre][S],dp[now][SS&(~1)]);
if( !(S&(1<<j)) && !(S&(1<<(j+1))) )
dp[now][SS^(1<<j)]=max(dp[pre][S]+v,dp[now][SS^(1<<j)]);
continue;
}
dp[now][S&(~(1<<j))]=max(dp[pre][S],dp[now][S&(~(1<<j))]);
if(!(S&(1<<j)) && !(S&(1<<(j-1))) && !(S&(1<<(j+1))) && !(S&(1<<(j+2))) )
dp[now][S^(1<<j)]=max(dp[pre][S]+v,dp[now][S^(1<<j)]);
}
}
nth_element(dp[now],dp[now]+total-1,dp[now]+total);
printf("%d\n",dp[now][total-1]);
}
} 模板化代码如下:
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
#define LL long long
const int maxn=100013;
int maze[16][16];
struct Node
{
int H[maxn];
int S[maxn];
int N[maxn];
int size;
void init()
{
size=0;
memset(H,-1,sizeof(H));
}
void push(int SS,int num)
{
int s=SS%maxn;
while( ~H[s] && S[H[s]]!=SS )
{
s++;
s%=maxn;
}
if(~H[s])
{
N[H[s]]=max(N[H[s]],num);
return;
}
N[size]=num;
S[size]=SS;
H[s]=size++;
}
} dp[2];
int now,pre;
int get(int S,int p,int l=1)
{
return (S>>(p*l))&((1<<l)-1);
}
void set(int &S,int p,int v,int l=1)
{
S^=get(S,p,l)<<(p*l);
S^=(v&((1<<l)-1))<<(p*l);
}
int main()
{
while(1)
{
int n=16;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
{
char ch;
if(scanf("%d%c",&maze[i][j],&ch)==-1) return 0;
if(ch=='\n' && n==16) n=j+1;
}
int now=1,pre=0;
dp[now].init();
dp[now].push(0,0);
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
swap(now,pre);
dp[now].init();
for(int s=0;s<dp[pre].size;s++)
{
int S=dp[pre].S[s];
int num=dp[pre].N[s];
if( get(S,j+1)==0
&& (j==0 || (get(S,j)==0 && get(S,j-1)==0))
&& get(S,j+2)==0 )
{
set(S,j,1);
dp[now].push(S,num+maze[i][j]);
}
set(S,j,0);
dp[now].push(S,num);
}
}
for(int s=0;s<dp[now].size;s++)
set(dp[now].S[s],n,0),dp[now].S[s]<<=1;
}
nth_element(dp[now].N,dp[now].N+dp[now].size-1,dp[now].N+dp[now].size);
printf("%d\n",dp[now].N[dp[now].size-1]);
}
}
HDU 1693 Eat the Trees
这题开始,就是真正的插头DP了。要搞清楚插头的概念,仍然建议看2008年国家集训队CDQ的论文:基于连通性状态压缩的动态规划问题
这题也没有那么难。每个插头两种状态,有或者无。用0,1记录即可,按照轮廓线逐格递推即可。代码如下:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
long long dp[2][1<<12];
int main()
{
int T;
int cas=1;
scanf("%d",&T);
while(T--)
{
int n,m;
scanf("%d%d",&n,&m);
int now=1;
int pre=0;
int total=1<<(m+1);
memset(dp[now],0,sizeof(dp[now]));
dp[now][0]=1;
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
int v;
scanf("%d",&v);
swap(now,pre);
memset(dp[now],0,sizeof(dp[now]));
int j0=1<<j;
int j1=j0<<1;
for(int S=0;S<total;S++) if(dp[pre][S])
{
if(v==0)
{
if( (S&j0)==0 && (S&j1)==0 )
dp[now][S]+=dp[pre][S];
continue;
}
dp[now][S^j0^j1]+=dp[pre][S];
if( ((S&j0)!=0)^((S&j1)!=0) )
{
dp[now][S]+=dp[pre][S];
}
}
}
swap(now,pre);
memset(dp[now],0,sizeof(dp[now]));
for(int S=0;S<total/2;S++) if(dp[pre][S])
{
dp[now][(S<<1)&(total-1)]+=dp[pre][S]; // new line
}
}
printf("Case %d: There are %I64d ways to eat the trees.\n",cas++,dp[now][0]);
}
} 模板化代码:
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
#define LL long long
const int maxn=2053;
int maze[16][16];
struct Node
{
int H[maxn];
int S[maxn];
LL N[maxn];
int size;
void init()
{
size=0;
memset(H,-1,sizeof(H));
}
void push(int SS,LL num)
{
int s=SS%maxn;
while( ~H[s] && S[H[s]]!=SS )
{
s++;
s%=maxn;
}
if(~H[s])
{
N[H[s]]+=num;
return;
}
N[size]=num;
S[size]=SS;
H[s]=size++;
}
LL get(int SS)
{
int s=SS%maxn;
while( ~H[s] && S[H[s]]!=SS)
{
s++;
s%=maxn;
}
if(~H[s])
return N[H[s]];
else
return 0;
}
} dp[2];
int now,pre;
int get(int S,int p,int l=1)
{
return (S>>(p*l))&((1<<l)-1);
}
void set(int &S,int p,int v,int l=1)
{
S^=get(S,p,l)<<(p*l);
S^=(v&((1<<l)-1))<<(p*l);
}
int main()
{
int T;
int cas=1;
scanf("%d",&T);
while(T--)
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
scanf("%d",&maze[i][j]);
now=1,pre=0;
dp[now].init();
dp[now].push(0,1);
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
swap(now,pre);
dp[now].init();
for(int s=0;s<dp[pre].size;s++)
{
int S=dp[pre].S[s];
LL num=dp[pre].N[s];
int p=get(S,j);
int q=get(S,j+1);
if(maze[i][j]==0)
{
if(p==0 && q==0)
dp[now].push(S,num);
continue;
}
if(p==0 && q==0)
{
if(maze[i][j+1] && maze[i+1][j])
{
set(S,j,1);
set(S,j+1,1);
dp[now].push(S,num);
}
}
else if(p^q)
{
if(maze[i+p][j+q])
dp[now].push(S,num);
set(S,j,q);
set(S,j+1,p);
if(maze[i+q][j+p])
dp[now].push(S,num);
}
else
{
set(S,j,0);
set(S,j+1,0);
dp[now].push(S,num);
}
}
}
for(int s=0;s<dp[now].size;s++)
dp[now].S[s]<<=1;
}
printf("Case %d: There are %I64d ways to eat the trees.\n",cas++,dp[now].get(0));
}
}
Ural 1519 Formula 1
#include <cstdio>
#include <cstring>
#include <iostream>
#include <map>
#include <algorithm>
using namespace std;
#define LL long long
LL dp[2][1<<24];
int state[2][1<<24];
int top[2];
int now,pre;
int endx,endy;
bool maze[15][15];
int m,n;
LL ans;
const int HASH = 1000037;
int Hash[HASH];
int save[HASH];
void HashIn(int S,LL num)
{
int s=S%HASH;
while(~Hash[s] && save[s]!=S)
{
s++;
s%=HASH;
}
if(Hash[s]==-1)
{
dp[now][top[now]]=num;
state[now][top[now]]=S;
Hash[s]=top[now];
save[s]=S;
top[now]++;
}
else
{
dp[now][Hash[s]]+=num;
}
}
void init()
{
memset(maze,0,sizeof(maze));
endx=-1;
for(int i=0;i<n;i++)
{
char str[200];
memset(str,0,sizeof(str));
scanf("%s",str);
for(int j=0;j<m;j++)
{
if(str[j]=='*')
{
maze[i][j]=0;
}
else if(str[j]=='.')
{
maze[i][j]=1;
endx=i;
endy=j;
}
}
}
}
// 位运算,取S按长度l的第p位
int getV(int S,int p,int l=2)
{
return (S>>(p*l))&((1<<l)-1);
}
// 位运算,设置S按长度l的第p位值为v
void setV(int& S,int p,int v,int l=2)
{
S^=getV(S,p)<<(p*l);
S|=v<<(p*l);
}
void memsetnow()
{
memset(Hash,-1,sizeof(Hash));
top[now]=0;
}
void solve()
{
init();
if(endx==-1)
{
puts("0");
return;
}
now=1;
pre=0;
ans=0;
memsetnow();
dp[now][0]=1;
state[now][0]=0;
top[now]=1;
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
int j2=j+j;
int j22=j2+2;
int j0=(1<<j2);
j0|=j0<<1;
int j1=j0<<2;
swap(now,pre);
memsetnow();
for(int s=top[pre]-1;s>=0;s--) if(dp[pre][s])
{
LL num=dp[pre][s];
int S=state[pre][s];
int p=getV(S,j);
int q=getV(S,j+1);
if(maze[i][j]==0)
{
if(p==0 && q==0)
{
HashIn(S,num);
}
continue;
}
if( (p>0) ^ (q>0) )
{
if(maze[i+(p>0)][j+(q>0)])
{
HashIn(S,num);
}
if(maze[i+(q>0)][j+(p>0)])
{
int nS=S;
setV(nS,j,q);
setV(nS,j+1,p);
HashIn(nS,num);
}
}
else if(p==0 && q==0)
{
if(maze[i+1][j]&&maze[i][j+1])
{
int nS=S;
setV(nS,j,1);
setV(nS,j+1,2);
HashIn(nS,num);
}
}
else if(p==1 && q==1)
{
int find=1;
for(int l=j+2;l<=m;l++)
{
int vv=getV(S,l);
if(vv==1)
find++;
else if(vv==2)
find--;
if(find==0)
{
int nS=S;
setV(nS,j,0);
setV(nS,j+1,0);
setV(nS,l,1);
HashIn(nS,num);
break;
}
}
}
else if(p==2 && q==2)
{
int find=1;
for(int l=j-1;l>=0;l--)
{
int vv=getV(S,l);
if(vv==2)
find++;
else if(vv==1)
find--;
if(find==0)
{
int nS=S;
setV(nS,j,0);
setV(nS,j+1,0);
setV(nS,l,2);
HashIn(nS,num);
break;
}
}
}
else if(p==2 && q==1)
{
int nS=S;
setV(nS,j,0);
setV(nS,j+1,0);
HashIn(nS,num);
}
else if(p==1 && q==2)
{
if(i==endx && j==endy)
ans+=num;
}
}
}
swap(now,pre);
memsetnow();
for(int s=0;s<top[pre];s++) if(dp[pre][s])
{
LL num=dp[pre][s];
int S=state[pre][s]<<2;
HashIn(S,num);
}
}
printf("%I64d\n",ans);
}
int main()
{
while(~scanf("%d%d",&n,&m))
{
solve();
}
}模板化代码如下:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define LL long long
const int maxn=100037; // 可能的最大状态数
struct Node
{
int H[maxn]; // 哈希
int S[maxn]; // 状态
LL N[maxn]; // 状态对应的数量
int size; // 总的状态数量
void init() // 初始化
{
memset(H,-1,sizeof(H));
size=0;
}
void push(int s,LL num) // 将状态压入,根据哈希的结果建立新状态或加在原有的状态上
{
int ss=s%maxn;
while( ~H[ss] && S[H[ss]]!=s )
{
ss++;
ss%=maxn;
}
if(H[ss]==-1)
{
S[size]=s;
N[size]=num;
H[ss]=size++;
}
else
{
N[H[ss]]+=num;
}
}
} dp[2];
int now,pre;
bool maze[13][13];
int endx,endy; // 记录最后一个可行位置
int m,n;
LL ans;
// 取S状态的第p位,每位l(不是1)个bit
int get(int S,int p,int l=2)
{
return (S>>(p*l))&((1<<l)-1);
}
// 置S状态的第p位为v,每位l(不是1)个bit
void set(int &S,int p,int v,int l=2)
{
S^=get(S,p,l)<<(p*l);
S^=(v&((1<<l)-1))<<(p*l);
}
// 输入地图
void input()
{
memset(maze,0,sizeof(maze));
endx=-1;
for(int i=0;i<n;i++)
{
char str[20];
scanf("%s",str);
for(int j=0;j<m;j++)
{
if(str[j]=='*')
{
maze[i][j] = false;
}
else if(str[j]=='.')
{
maze[i][j]=true;
endx=i;
endy=j;
}
}
}
}
void solve()
{
now=1;
pre=0;
ans=0;
dp[now].init();
dp[now].push(0,1);
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
swap(now,pre);
dp[now].init();
for(int s=0;s<dp[pre].size;s++)
{
int S=dp[pre].S[s];
LL num=dp[pre].N[s];
int p=get(S,j);
int q=get(S,j+1);
if(maze[i][j]==0) // 地图中不可走的点
{
if(p==0 && q==0)
{
dp[now].push(S,num);
}
continue;
}
if(p==0 && q==0) // 如果地图允许,构造新的连通块
{
if(maze[i+1][j] && maze[i][j+1])
{
set(S,j,1);
set(S,j+1,2);
dp[now].push(S,num);
}
}
else if( (p>0)^(q>0) ) // 左边和右边有一边有插头
{
if(maze[i+(p>0)][j+(q>0)])
{
dp[now].push(S,num);
}
if(maze[i+(q>0)][j+(p>0)])
{
set(S,j,q);
set(S,j+1,p);
dp[now].push(S,num);
}
}
else if( p==2 && q==1 ) // 结束连通块
{
set(S,j,0);
set(S,j+1,0);
dp[now].push(S,num);
}
else if( p==1 && q==1 ) // 寻找对应的2插头
{
int find=1;
for(int k=j+2;k<=m;k++)
{
int v=get(S,k);
if(v==2)
find--;
else if(v==1)
find++;
if(find==0)
{
set(S,j,0);
set(S,j+1,0);
set(S,k,1);
dp[now].push(S,num);
break;
}
}
}
else if( p==2 && q==2 ) // 寻找对应的1插头
{
int find=1;
for(int k=j-1;k>=0;k--)
{
int v=get(S,k);
if(v==1)
find--;
else if(v==2)
find++;
if(find==0)
{
set(S,j,0);
set(S,j+1,0);
set(S,k,2);
dp[now].push(S,num);
break;
}
}
}
else if( p==1 && q==2 ) // 结束
{
if(i==endx && j==endy)
ans+=num;
}
}
}
for(int s=0;s<dp[now].size;s++) // 换行
dp[now].S[s]<<=2;
}
}
int main()
{
while(~scanf("%d%d",&n,&m))
{
input();
if(endx==-1) {puts("0");continue;}
solve();
printf("%I64d\n",ans);
}
}
只前的模板一直都是用括号法。时间空间上都要比最小表示法好。无奈对于广义路径,括号序列就力不从心了。本题最小表示法如下:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int maxn=29989;
const int L=3;
int now,pre;
bool maze[15][15];
int endx,endy;
int code[15],ch[15];
int n,m;
LL ans;
struct Node
{
int H[maxn];
LL S[maxn];
LL N[maxn];
int size;
void init()
{
memset(H,-1,sizeof(H));
size=0;
}
void push(LL SS,LL num)
{
int s=SS%maxn;
while( ~H[s] && S[H[s]]!=SS )
s=(s+1)%maxn;
if( ~H[s] )
{
N[H[s]]+=num;
}
else
{
S[size]=SS;
N[size]=num;
H[s]=size++;
}
}
} dp[2];
LL encode()
{
memset(ch,-1,sizeof(ch));
ch[0]=0;
int cnt=1;
LL S=0;
for(int i=m;i>=0;i--)
{
if(ch[code[i]]==-1)
ch[code[i]]=cnt++;
code[i]=ch[code[i]];
S<<=L;
S|=code[i];
}
return S;
}
void decode(LL S)
{
for(int i=0;i<=m;i++)
{
code[i]=S&((1<<L)-1);
S>>=L;
}
}
void shift()
{
for(int s=0;s<dp[now].size;s++)
dp[now].S[s]<<=L;
}
void doGrid(int i,int j)
{
for(int s=0;s<dp[pre].size;s++)
{
LL S=dp[pre].S[s];
LL N=dp[pre].N[s];
decode(S);
int left=code[j];
int up=code[j+1];
int mi=min(left,up);
int ma=max(left,up);
if(maze[i][j]==0)
{
if(ma==0) dp[now].push(encode(),N);
continue;
}
if(ma==0)
{
if(maze[i][j+1] && maze[i+1][j])
{
code[j]=code[j+1]=13;
dp[now].push(encode(),N);
}
}
else if(mi==0)
{
if(maze[i+1][j])
{
code[j]=ma;
code[j+1]=0;
dp[now].push(encode(),N);
}
if(maze[i][j+1])
{
code[j]=0;
code[j+1]=ma;
dp[now].push(encode(),N);
}
}
else if(left==up)
{
if(i==endx && j==endy)
ans+=N;
}
else
{
code[j]=code[j+1]=0;
for(int k=0;k<=m;k++)
if(code[k]==up)
code[k]=left;
dp[now].push(encode(),N);
}
}
}
void solve()
{
now=1;
pre=0;
ans=0;
dp[now].init();
dp[now].push(0,1);
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
swap(now,pre);
dp[now].init();
doGrid(i,j);
}
shift();
}
}
void init()
{
memset(maze,0,sizeof(maze));
endx=-1;
char str[20];
for(int i=0;i<n;i++)
{
scanf("%s",str);
for(int j=0;j<m;j++) if(str[j]=='.')
maze[i][j]=1,endx=i,endy=j;
}
}
int main()
{
while(~scanf("%d%d",&n,&m))
{
init();
if(endx==-1) {puts("0");continue;}
solve();
printf("%I64d\n",ans);
}
} 最小表示法,简单来说就是数字相同代表连通。每次通过decode读取状态,通过encode将状态转为二进制数。因为12*12的棋盘最多只有6对插头,所以使用3进制(7个插头)。
结束?
好了,入门结束了,插头DP才刚开始。接下来推荐刷Kuangbin大神的题表:http://www.cnblogs.com/kuangbin/archive/2012/10/02/2710343.html。大家A的开心。
插头DP的广义路径建议看CDQ的论文(非PPT),以及NotOnlySuccess的博客:http://www.notonlysuccess.com/index.php/plug-dp-complete/
转载注明出处:SF-_-: http://blog.csdn.net/sf____