CCActionEase(2)

本文函数图像使用GeoGebra绘制，感谢它才华横溢的作者。

相比之前的速度正弦变化动作（这个东西叫什么更好一些？渐变动画？）与速度指数级变化动作，CCEaseIn/CCEaseOut/CCEaseInOut更具灵活性。你可以设置运动的速率，甚至是在运动的过程中改变速率。它们拥有共同的基类——CCEaseRateAction。不要直接使用CCEaseRateAction，因为它没有实现任何变化效果。

7)CCEaseIn

按照惯例贴出update函数的源代码，以免版本更新导致文不对题。

1 void CCEaseIn::update(ccTime time)
2 {
3     m_pOther->update(powf(time, m_fRate));
4 }

根据此函数的实现推导出以下三个公式：

s(t)=t^r t∈[0,1]
v(t)=s'(t)=r*t^(r-1) t∈[0,1]
a(t)=v'(t)=r*(r-1)*t^(r-2) t∈[0,1]

s:路程 v:速度 a:加速度 t:时间 r:速率参数m_fRate
都是很基本的导函数推导，如果有不清楚的地方，建议先复习下导数。

下面我们着重分析下速率参数，也就是r的取值范围。因为是讨论二元函数，图像是三维的，画出后重叠在一起反而不利于理解，这里就没有作图。

1.r<0

当r<0时，v(t)将始终保持为负数，也就是说速度的方向与设定的方向正好相反。
又因为s(1)=1，这说明精灵最后移动到了目标点坐标，但它是从预设轨迹的延长线上反向移动到这一坐标点的。
这是一个很奇怪的动作行为，跟我们预想的设计不符，所以r的取值不应小于零。

2.r=0

当r=0时，s(t)恒等于1，也就说动作在开始之前就已经达到了完成的状态。我们这里说的是动作的表现，动作原本的执行时间是不受此影响的。
很明显，这与我们的设计不符，所以零也不是r的一个取值。

3.0<r<1

当r的取值范围在(0,1)时，a(t)恒为负数，加速度为负说明速度是越来越慢的，这与CCEaseXxxxIn动作应该由慢至快的设定不符，所以这也不是r应有的取值范围。

4.r=1

当r=1时，a(t)恒等于零，v(t)恒等于一，这说明此时的动作是速度为1的匀速运动。这貌似与设定的有慢至快也不相符。

5.1<r<2

当r的取值范围在(1,2)时，加速度a(t)恒大于零，但呈下降趋势。

6.r=2

当r=2是，a(t)恒等于2，也就是此时为匀加速运动。

7.r>2

当r>2时，加速度a(t)恒大于零，且呈上升趋势。

综上所述，当你使用CCEaseIn时，传入的速率参数应大于1.0f，并且根据取值范围的不同，会呈现出3种不太一样的加速运动。

8)CCEaseOut

我们再来看一下CCEaseOut的update函数。

1 void CCEaseOut::update(ccTime time)
2 {
3     m_pOther->update(powf(time, 1 / m_fRate));
4 }

第一步还是需要推导出路程、速度、加速度的公式：

s(t)=t^(1/r) t∈[0,1]
v(t)=s'(t)=1/r*(t^(1/r-1)) t∈[0,1]
a(t)=v'(t)=1/r*(1/r-1)*(t^(1/r-2)) t∈[0,1]

第二步分析r的取值范围：

1.r<0

当r<0时，CCEaseOut的情况与CCEaseIn一样，运动不在预设轨迹上，排除。

2.r=0

除数不能为零，排除。

3.0<r<1

当r的取值范围在(0,1)时，a(t)恒大于零，这说明速度是越来越快的，这与CCEaseXxxxOut由快至慢的设定不符，排除。

4.r=1

当r=1时，a(t)恒等于零，这说明是匀速运动，不符合设定，排除。

5.r>1

当r>1时，加速度a(t)恒小于零，但呈上升趋势。

综上所述，当你使用CCEaseOut时，传入的速率参数应大于1.0f，与CCEaseIn不同的是，CCEaseOut只有一类加速度变化趋势。

在继续后面的研究之前，我们来做一些额外的思考。CCEaseOut中r的取值为什么与CCEaseIn的有些不一样呢？是不是它的设计存在什么不合理的地方？

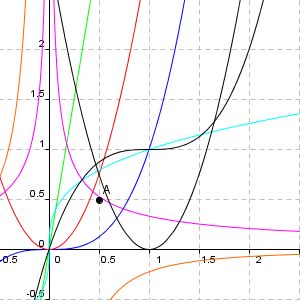
假设我们将r设定为3，同时画出CCEaseIn和CCEaseOut的图像：

颜色有点儿乱，不过没办法，里面包含3套对比数据，我直接说颜色，希望大家别迷糊。

那条红色曲线是CCEaseIn的v(t)函数，那条分数的是CCEaseOut的v(t)函数。
大家都知道CCEaseXxxxIn与CCEaseXxxxOut动作的区别是，前者由慢到快，后者由快到慢。如果说得更精确些，它们的表现应该是对称的——速度函数v(t)按照x=0.5直线轴对称。
但是显而易见的，红色曲线和粉色曲线根本不对称。

如果大家再仔细想想之前正弦变化和指数级变化的图像，这里还存在一处对称。那就是，路程函数s(t)的图像应该是按照点A(0.5,0.5)中心对称的。
那条蓝色曲线是CCEaseIn的s(t)函数，那条兰色的是CCEaseOut的s(t)函数。
可以很明显地看出，它们是按照y=x直线轴对称的，而不是按照点A中心对称。

我们将红色曲线按照x=0.5直线做轴对称镜像，得到那条黑色的抛物线。再对此抛物线求其反导函数图像，得到那条黑色曲线。瞧，它与那条蓝色曲线是不是按照点A中心对称的。
所以，我认为CCEaseOut的update函数应该修改一下。如果你有不同的见解，欢迎在评论区留言。

附上我修改后的代码：

1 void CCEaseOut::update(ccTime time)
2 {
3     m_pOther->update(1.0f - powf((1.0f - time), m_fRate));
4 }

如果按我这样修改，那么速率参数的取值范围与CCEaseIn中是一样的，大于一。

9)CCEaseInOut

好了，继续我们的研究：

 1 void CCEaseInOut::update(ccTime time)
 2 {
 3     int sign = 1;
 4     int r = (int) m_fRate;
 5 
 6     if (r % 2 == 0)
 7     {
 8         sign = -1;
 9     }
10 
11     time *= 2;
12     if (time < 1)
13     {
14         m_pOther->update(0.5f * powf(time, m_fRate));
15     }
16     else
17     {
18         m_pOther->update(sign * 0.5f * (powf(time - 2, m_fRate) + sign * 2));
19     }
20 }

必须指出，这个函数的实现是有问题的。

第一，难道引擎的设计者只希望我们传入整数型的速率吗？
问题出在powf函数调用上。
我们知道传入的time参数范围在[0,1]，即便中间做了一次乘2的操作，到了后面time-2依然是小于等于零的。所以在某些情况下，powf会出现问题。
比如，当m_fRate设置为3.5f之类的小数时，这里的powf会返回"-1.#IND000"。
于是，当动作执行到后半段时，精灵会消失，直到动作全部完成，精灵才会出现在终点上。

第二，那个sign正负标志是用来解决问题的吗？怎么感觉引入后反而将问题复杂化了。
这里其实只需将前半段的函数按照点(0.5,0.5)做一次中点对称就可以了，用不着这么麻烦。
我修改的代码如下：

 1 void CCEaseInOut::update(ccTime time)
 2 {
 3     time *= 2;
 4     if (time < 1)
 5     {
 6         m_pOther->update(0.5f * powf(time, m_fRate));
 7     }
 8     else
 9     {
10         m_pOther->update(0.5f * (2.0f - powf((2.0f - time), m_fRate)));
11     }
12 }

因为CCEaseInOut与CCEaseIn使用相同的算法，所以在这里速率参数的取值范围与CCEaseIn的一样，也是大于一。

小结

到目前为止，我们对CCActionEase的学习已经完成了一半。

我们一共学习了3类，9个动作。它们分别是CCEaseSineIn、CCEaseSineOut、CCEaseSineInOut、CCEaseExponentialIn、CCEaseExponentialOut、CCEaseExponentialInOut、CCEaseIn、CCEaseOut、CCEaseInOut。

它们与之后将要学习的动作的最大区别是，在这些动作的执行过程中，精灵会严格地按照内部动作指定的路径移动，绝对不会超出起始点与终点的范围。

在CCEaseIn/CCEaseOut/CCEaseInOut中，速度的变化范围是[0,m_fRate]，m_fRate>1。

但是，如果cocos2d-x需要与cocos2d-iphone从原则上保持高度一致，即便是存在缺陷也不能破坏原则的话，那么我推测官方在短时间内是不会修改这个问题的。因为，在大约6个月之前，有朋友提出过此问题，但似乎被无视了。
http://www.cocos2d-iphone.org/forum/topic/20979
http://code.google.com/p/cocos2d-iphone/issues/detail?id=1248

所以，在官方正式修正此问题之前，我建议大家只使用大于1的整数作为速率的参数，以提高兼容性。