数据结构基础 之 图 的 邻接矩阵实现与邻接表实现

【邻接矩阵】

邻接矩阵，就是一个反应边与边之间联系的二维数组。这个二维数组我们用matrix[numV][numV]表示，其中numV是顶点数。

对于无权图

若顶点Vi和Vj之间有边，则matrix[Vi][Vj]=1;否则matrix[Vi][Vj]=0。

对于有权图

若顶点Vi和Vj之间有边，且权值为weight，则matrix[Vi][Vj]=weight;否则matrix[Vi][Vj]=0或MAXWEIGHT(取最小权值或最大权值)。

【邻接表】

当图中的边数较少时，用邻接矩阵来实现图结构，则会浪费很多内存空间。因此，考虑另一种实现图结构的方法：邻接表。在邻接表中主要有两种节点结构体：

顶点节点（（vertex）表示节点数据，也可以是节点下标；以及下一节点地址（next））

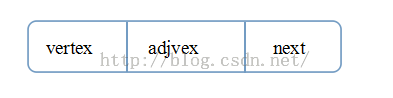
边节点（（vertex）表示节点数据，也可以是节点下标；（adjvex）通俗理解就是（vertex）节点出度表；以及出度表中下一出度节点地址（next））

【源码示例】

• 邻接矩阵建图

void Graph::createGraph()  
{  
    cout << "输入边数 ";  
    while (cin >> numE && numE < 0)  
        cout << "输入有误！，重新输入 ";  
  
    int i, j, w;  
    if (!isWeighted)  //无权图  
    {  
        if (!isDirected)  //无向图  
        {  
            cout << "输入每条边的起点和终点：\n";  
            for (int k = 0; k < numE; k++)  
            {  
                cin >> i >> j;  
                while (!check(i, j))  
                {  
                    cout << "输入的边不对！重新输入\n";  
                    cin >> i >> j;  
                }  
                matrix[i][j] = matrix[j][i] = 1;  
            }  
        }  
        else  //有向图  
        {  
            cout << "输入每条边的起点和终点：\n";  
            for (int k = 0; k < numE; k++)  
            {  
                cin >> i >> j;  
                while (!check(i, j))  
                {  
                    cout << "输入的边不对！重新输入\n";  
                    cin >> i >> j;  
                }  
                matrix[i][j] = 1;  
            }  
        }  
    }  
    else  //有权图  
    {  
        if (!isDirected)   //无向图  
        {  
            cout << "输入每条边的起点、终点和权值：\n";  
            for (int k = 0; k < numE; k++)  
            {  
                cin >> i >> j >> w;  
                while (!check(i, j, w))  
                {  
                    cout << "输入的边不对！重新输入\n";  
                    cin >> i >> j >> w;  
                }  
                matrix[i][j] = matrix[j][i] = w;  
            }  
        }  
        else  //有向图  
        {  
            cout << "输入每条边的起点、终点和权值：\n";  
            for (int k = 0; k < numE; k++)  
            {  
                cin >> i >> j >> w;  
                while (!check(i, j, w))  
                {  
                    cout << "输入的边不对！重新输入\n";  
                    cin >> i >> j >> w;  
                }  
                matrix[i][j] = w;  
            }  
        }  
    }  
} 

• 邻接表建图

void Graph::createGraph()  
{  
    //用一个新的变量表示边数，numE的修改则留到insertedge()中  
    int numEdge = 0;  
    cout << "输入边数 ";  
    while (cin >> numEdge && numEdge < 0)  
        cout << "输入有误！，重新输入 ";    
    int i, j, w;  
    if (!isWeighted)  //无权图  
    {  
        cout << "输入每条边的起点和终点：\n";  
        for (int k = 0; k < numEdge; k++)  
        {  
            cin >> i >> j;  
            while (!check(i, j))  
            {  
                cout << "输入的边不对！重新输入\n";  
                cin >> i >> j;  
            }  
            insertEdge(i, j);  
        }  
    }  
    else  //有权图  
    {  
        cout << "输入每条边的起点、终点和权值：\n";  
        for (int k = 0; k < numEdge; k++)  
        {  
            cin >> i >> j >> w;  
            while (!check(i, j, w))  
            {  
                cout << "输入的边不对！重新输入\n";  
                cin >> i >> j >> w;  
            }  
            insertEdge(i, j, w);  
        }  
    }  
}  
void Graph::insertEdge(int vertex, int adjvex, int weight)  
{  
    insertedge(vertex, adjvex, weight);  
    if (!isDirected)  //无向图  
        insertedge(adjvex, vertex, weight);  
}  
void Graph::insertedge(int vertex, int adjvex, int weight)  
{  
    EdgeNode *p, *q, *r;
    p = q = r = NULL;  
    if (adjList[vertex].next)   //非第一个节点  
    {  
        p = adjList[vertex].next;  
        //移动p到合适位置  
        while (p && (p->adjvex < adjvex))  
        {  
            q = p;  
            p = p->next;  
        }  
        if (p && (p->adjvex == adjvex))  //修改已有边权值  
            p->weight = weight;  
        else  
        {  
            r = new EdgeNode;  
            r->adjvex = adjvex;  
            r->weight = weight;  
            r->next = p;  
            //当加入的新节点位于表的第一个位置  
            if (adjList[vertex].next == p)  
                adjList[vertex].next = r;  
            else  
                q->next = r;  
            numE++;  
        }  
    }  
    else  
    {  
        p = new EdgeNode;  
        p->adjvex = adjvex;  
        p->weight = weight;  
        p->next = NULL;  
        adjList[vertex].next = p;  
        numE++;  
    }  
}  

【详细源码详址】

http://blog.csdn.net/zhangxiangdavaid/article/details/38321327

http://blog.csdn.net/zhangxiangdavaid/article/details/38323593

【最后的话】

很明显的发现，邻接矩阵和邻接表一个是以矩阵数组的形式记录了图中边的关系，一个是以链表数组的形式记录边的关系。无它，链表肯定比数据更节省空间，但是，查找操作数组往往比链表更快捷。如果，还有兴趣可以用STL的 list 实现，这样将尽收二者之长，鉴于实现非常简单，此处代码就不再给出。

【注】

list，vector是push_back，queue和stack是push 。