哈夫曼树详解<续>
上面介绍到最小堆的模板实现以及模板的使用情况,这篇中就如何构造 一个哈夫曼树的核心算法思想作介绍。
一棵哈夫曼树的结点有带不带权值之分,也就是内外结点之分,所以在这里用了一个枚举类型enum_modes,标示内外结点的。
在构造哈夫曼树(HuffmanTree<T>)时,定义了一个最小堆,类型就是哈夫曼树结点(HuffmanTreeNode<T>)类型。
下面贴源码:
首先是枚举类型:
#pragma once
enum position_modes{inside, outside};哈夫曼树结点类型:
仍然是大量的重载函数,不过这里有一些没用到
#pragma once
#include<iostream>
#include"enum_modes.h"
using namespace std;
template<class T>
class HuffmanTreeNode
{
public:
T data; //HuffmanTree的虚拟类型
position_modes flag; //位置标示,表明该结点是扩充二叉树中是外结点还是内结点
HuffmanTreeNode<T> *LeftChild, *RightChild, *Parent; //结点的左右孩子和双亲
public:
HuffmanTreeNode();
HuffmanTreeNode(T elem, position_modes fg, HuffmanTreeNode<T> *left = NULL, HuffmanTreeNode<T> *right = NULL, HuffmanTreeNode<T> *par = NULL);
bool operator<= (HuffmanTreeNode<T> &HTNode);
bool operator>= (HuffmanTreeNode<T> &HTNode);
bool operator> (HuffmanTreeNode<T> &HTNode);
bool operator< (HuffmanTreeNode<T> &HTNode);
void operator= (HuffmanTreeNode<T> &HTNode); //赋值重载
template<class T> friend ostream& operator<< (ostream &output, HuffmanTreeNode<T> &HTNode);
};
template<class T>
HuffmanTreeNode<T>::HuffmanTreeNode()
{
flag = inside;
LeftChild = NULL;
RightChild = NULL;
Parent = NULL;
}
template<class T>
HuffmanTreeNode<T>::HuffmanTreeNode(T elem, position_modes fg = inside, HuffmanTreeNode<T> *left = NULL, HuffmanTreeNode<T> *right = NULL, HuffmanTreeNode<T> *par = NULL)
{
data = elem;
flag = fg
LeftChild = left;
RightChild = right;
Parent = par;
}
template<class T>
bool HuffmanTreeNode<T>::operator<= (HuffmanTreeNode<T> &HTNode)
{
return ((this->data <= HTNode.data) ? true : false);
}
template<class T>
bool HuffmanTreeNode<T>::operator>= (HuffmanTreeNode<T> &HTNode)
{
return ((this->data >= HTNode.data) ? true : false);
}
template<class T>
bool HuffmanTreeNode<T>::operator> (HuffmanTreeNode<T> &HTNode)
{
return ((this->data > HTNode.data) ? true : false);
}
template<class T>
bool HuffmanTreeNode<T>::operator< (HuffmanTreeNode<T> &HTNode)
{
return ((this->data < HTNode.data) ? true : false);
}
template<class T>
void HuffmanTreeNode<T>::operator= (HuffmanTreeNode<T> &HTNode)
{
this->data = HTNode.data;
this->flag = HTNode.flag;
this->LeftChild = HTNode.LeftChild;
this->RightChild = HTNode.RightChild;
this->Parent = HTNode.Parent;
}
template<class T>
ostream& operator<< (ostream &output, HuffmanTreeNode<T> &HTNode)
{
output<<HTNode.data<<" "<<HTNode.flag<<" "<<HTNode.LeftChild<<" "<<HTNode.RightChild<<" "<<HTNode.Parent;
return output;
}
#pragma once
#include"HuffmanTreeNode.h"
#include"MinHeap.h"
#include<iostream>
using namespace std;
template<class T>
class HuffmanTree
{
protected:
HuffmanTreeNode<T> *root; //HuffmanTree的根结点
void Display(ostream& output, HuffmanTreeNode<T> *subTree); //输出一棵哈夫曼树
void DeleteTree(HuffmanTreeNode<T> *subTree); //销毁一棵哈夫曼树
void MergeTree(HuffmanTreeNode<T> htNode1, HuffmanTreeNode<T> htNode2, HuffmanTreeNode<T> * &parent); //合并两颗子树
public:
HuffmanTree();
HuffmanTree(T arr[], int elemnum); //构造出来一棵哈夫曼树
~HuffmanTree();
template<class T> friend ostream& operator<< (ostream &output, HuffmanTree<T> &HT); //标准输出重载
};
template<class T>
void HuffmanTree<T>::Display(ostream& output, HuffmanTreeNode<T> *subTree)
{
if(subTree != NULL)
{
//if(subTree->flag == inside)
//{
output<<subTree->data<<" "; //输出结点
output<<subTree->flag<<endl; //输出内或外结点标示
//}
Display(output, subTree->LeftChild);
Display(output, subTree->RightChild);
}
}
template<class T>
void HuffmanTree<T>::DeleteTree(HuffmanTreeNode<T> *subTree)
{
if(subTree != NULL)
{
DeleteTree(subTree->LeftChild);
DeleteTree(subTree->RightChild);
delete subTree;
}
}
template<class T>
HuffmanTree<T>::HuffmanTree()
{
//
}
template<class T>
HuffmanTree<T>::~HuffmanTree()
{
DeleteTree(root);
}
template<class T>
HuffmanTree<T>::HuffmanTree(T arr[], int elemnum) //接受的是一个自定义类型的数组
{
MinHeap<HuffmanTreeNode<T>> mhp(elemnum); //在这里 先需要一个小顶堆 用来存储森林(即为每一个HuffmanTreeNode)
HuffmanTreeNode<T> *parent = NULL, first_min, second_min, temp; //一个用于牵引两个最小子树的结点父指针,当前最小的树,次小的树,一个临时结点变量
for(int idx = 0; idx < elemnum; idx++)
{
temp.data = arr[idx]; //先把结点数据赋进去
temp.flag = inside; //这里的标示都要是 内结点
temp.LeftChild = NULL; //刚开始 所有的内结点的三个指针域全为NULL
temp.RightChild = NULL;
temp.Parent = NULL;
mhp.Insert(temp); //把这么一个已处理好的HuffmanTreeNode放进堆中
}
for(int i = 0; i < elemnum - 1; i++) //N个树的森林 需要做N-1次就能构造出一棵哈夫曼树
{
mhp.RemoveMinelem(first_min);
mhp.RemoveMinelem(second_min); //获取堆中当前两个较小的HuffmanTreeNode
MergeTree(first_min, second_min, parent); //把两个较小的拿来进行合并成一棵树,用parent指针做牵引
mhp.Insert(*parent); //新生成的parent指针指向的HuffmanTreeNode也要放进小顶堆中 进行排序
}
root = parent; //当森林中只剩下一棵树的时候,这棵树就是哈夫曼树了,把此时的parent指针赋给root
}
template<class T>
void HuffmanTree<T>::MergeTree(HuffmanTreeNode<T> htNode1, HuffmanTreeNode<T> htNode2, HuffmanTreeNode<T> * &parent)
{ //在这里要强调的是:两个结点变量一定要用值传递的形式,因为外面的两个实参变量是地址不变的,不能拿来用,只能拷贝一份用
//这里的父指针,一定要用指针类型的引用才行,即为合并函数中的parent与外部实参parent实质上是一个值 这样才能做到正确的牵引
parent = new HuffmanTreeNode<T>; //开辟一个结点给外部实参parent
parent->LeftChild = new HuffmanTreeNode<T>(htNode1); //这里要强调的是,不能直接把形参表里的结点拿来赋地址,因为形参表中的是局部变量,当这个合并函数调用结束后,他们就释放掉了,所以在这里要根据形参值深度拷贝一份一样的,把返回的指针赋给父指针
parent->RightChild = new HuffmanTreeNode<T>(htNode2);
parent->flag = outside; //这里的父指针所指向的结点都是外结点
parent->data = htNode1.data + htNode2.data; //数据相加
parent->LeftChild->Parent = parent->RightChild->Parent = parent; //将两个子树结点的父指针域赋上当前的parent(就是牵引他们的指针)
}
template<class T>
ostream& operator<< (ostream &output, HuffmanTree<T> &HT)
{
HT.Display(output, HT.root); //内部调用 递归输出一棵哈夫曼树
return output;
}
下面是自定义类:
#pragma once
#include<iostream>
#include<fstream>
using namespace std;
class Code
{
private:
char ch_code; //字符码
float probability; //使用概率
public:
Code();
Code(char ch, float pro);
friend ostream& operator<< (ostream &output, Code &C);
friend istream& operator>> (istream &input, Code &C);
friend ofstream& operator<< (ofstream &foutput, Code &C);
friend ifstream& operator>> (ifstream &finput, Code &C);
bool operator<= (Code &C);
bool operator>= (Code &C);
bool operator> (Code &C);
bool operator< (Code &C);
friend Code operator+ (Code &C1, Code &C2);
void operator= (Code &C);
};
#include"Code.h"
#include<fstream>
using namespace std;
Code::Code()
{
}
Code::Code(char ch, float pro)
{
ch_code = ch;
probability = pro;
}
ostream& operator<< (ostream &output, Code &C)
{
output<<"编码值:"<<C.ch_code<<" "<<"编码值使用概率:"<<C.probability;
return output;
}
istream& operator>> (istream &input, Code &C)
{
input>>C.ch_code>>C.probability;
return input;
}
ofstream& operator<< (ofstream &foutput, Code &C)
{
foutput<<C.ch_code<<" "<<C.probability;
return foutput;
}
ifstream& operator>> (ifstream &finput, Code &C)
{
finput>>C.ch_code>>C.probability;
return finput;
}
Code operator+ (Code &C1, Code &C2)
{
return Code('#',(C1.probability + C2.probability));
}
void Code::operator= (Code &C)
{
this->ch_code = C.ch_code;
this->probability = C.probability;
}
bool Code::operator<= (Code &C)
{
return ((this->probability <= C.probability) ? true : false);
}
bool Code::operator>=(Code &C)
{
return ((this->probability >= C.probability) ? true : false);
}
bool Code::operator> (Code &C)
{
return ((this->probability > C.probability) ? true : false);
}
bool Code::operator<(Code &C)
{
return ((this->probability < C.probability) ? true : false);
}
下面是主函数调用代码:
Code c[5]; //自定义类对象数组
ifstream in("CODE.txt"); //依旧存在文件中
for(int i = 0; i < 5; i++)
{
in>>c[i]; //文件输入流
}
HuffmanTree<Code> ht1(c, 5); //传输组 构造哈夫曼树
cout<<ht1<<endl; //输出一棵哈夫曼树
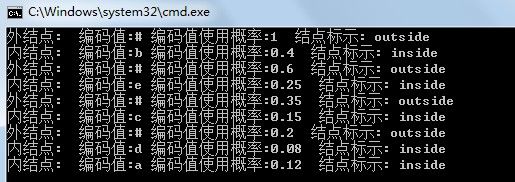
图中的外结点没有意义,只有内结点才是目标结点。
最后分享一下关于C++内存管理的心得吧,我想让任何一个C++程序员说出其在学习C++的过程中最痛苦的是什么,我想大部分应该会说是C++的内存管理吧。确实,相对于Java与C#这些语言来说,C++被定义为不安全的语言。然而哲学上相当讲究的就是一个事物的两面性,C++也不例外,他的内存管理过于繁琐,因此也有不少的C++程序员为之“倾倒”。但这也注定会带来开发过程中的好处,至于这些好处身在学生时代的我是感受颇少,但我相信好处是有的,要不然C++也不会从80年代初期问世以来一直是有用武之地的。
最近一段时间,看了很多的树的代码,也写了很多,过程中思考了更多。在这里做个总结
就以二叉树为例,前序递归遍历生成一棵二叉树的算法中,看这段代码
template<class T>
void BinTree<T>::CreateBinTree_(ifstream& in,BT_Node<T> * &subTree) //文件流输入重载 适用于从文件中读进内存
{
T item;
if(!in.eof())//不到文件的末尾 执行
{
in>>item;
if(item != endflag_value)
{
subTree = new BT_Node<T>(item);//调用含参 构造函数 指针域为NULL
if(subTree == NULL)
{
cout<<"内存分配错误!"<<endl;
exit(1);//强制结束进程
}
CreateBinTree_(in,subTree->leftchild);//递归调用 建立当前结点为根结点的左右子树
CreateBinTree_(in,subTree->rightchild);
}
else
subTree = NULL;//把当前参数中的指针置为NULL 封闭子树指针域
}
}参数中的子树指针用的是引用形式,大家有没有试过把那个引用去掉呢?我就在刚开始写的过程中没有注意那么多,想当然的忽略掉了,然而造成的后果却是致命的。
分析如下:这就是函数的参数是否为引用的一个区别了,如果没有这个引用的话,每次递归的时候把当前函数中的subTree->leftchild放进参数列表进行递归,仅仅是简单的值传递。在栈中处理函数递归的这个非引用形参是一个局部变量,把一个新开辟空间给了一个局部变量这是一个很可怕的事情,当递归回到上一层,这个局部变量也就消失了,那么这块内存就成为内存“黑洞”了。最后的结果是虽然没有语法错误,运行起来也没错,但是当你输出一棵二叉树的时候会发现,内存访问冲突,这种问题十有八九就是访问了不存在的内存地址。
现在换成引用会怎么样呢?在当前函数中,把subTree->leftchild以引用的形式传递给下一层函数,那么在下一层函数中开辟的空间就赋给了这个引用,也就是下层节点空间空间与上层指针真正建立了联系。以此递归下去,一棵树就这么出来了。在递归的时候参数使用指针的引用形式一般是为了上下层之间正确的建立关系。
再来说说我在写哈夫曼树的时候的窘境吧:
看这段代码:也是上下层之间建立联系的
template<class T>
void HuffmanTree<T>::MergeTree(HuffmanTreeNode<T> htNode1, HuffmanTreeNode<T> htNode2, HuffmanTreeNode<T> * &parent)
{ //在这里要强调的是:两个结点变量一定要用值传递的形式,因为外面的两个实参变量是地址不变的,不能拿来用,只能拷贝一份用
//这里的父指针,一定要用指针类型的引用才行,即为合并函数中的parent与外部实参parent实质上是一个值 这样才能做到正确的牵引
parent = new HuffmanTreeNode<T>; //开辟一个结点给外部实参parent
parent->LeftChild = new HuffmanTreeNode<T>(htNode1); //这里要强调的是,不能直接把形参表里的结点拿来赋地址,因为形参表中的是局部变量,当这个合并函数调用结束后,他们就释放掉了,所以在这里要根据形参值深度拷贝一份一样的,把返回的指针赋给父指针
parent->RightChild = new HuffmanTreeNode<T>(htNode2);
parent->flag = outside; //这里的父指针所指向的结点都是外结点
parent->data = htNode1.data + htNode2.data; //数据相加
parent->LeftChild->Parent = parent->RightChild->Parent = parent; //将两个子树结点的父指针域赋上当前的parent(就是牵引他们的指针)
}
参数列表中的最后一个参数用的是指针的引用形式和二叉树递归建立的目的是一样的,不使用的后果也是严重的。
我们的数据结构教材是C++版《殷人昆》的,感觉不是一般的坑,所有只是看里面的思想,一般代码都是按照自己的风格与习惯敲的,再加上百度这个神器。教材上的代码中,参数列表中的HuffmanTreeNode类对象用的是引用,后来发现这是错误的。
为什么不能用引用?分析如下,在HuffmanTree的构造函数中,有两个变量first_min,second_min。这两个是用来接受最小堆中的两个较小的元素的,这没有错,错就在下一步
MergeTree(first_min, second_min, parent); //把两个较小的拿来进行合并成一棵树,用parent指针做牵引如果是引用,那么形参实参共用内存段,在将htNode1与htNode2的地址赋给parent时,赋的就是这两个first_min,second_min的地址。结果是,很多父结点所指向的都是这两个变量的地址。然而也不能用htNode1与htNode2的地址,因为这两个变量仍然是局部函数变量,一旦函数生命周期结束,在栈中的变量就会被释放掉的。所以,最后想了一下用了一个深度复制来解决这个问题。这样子,尽管htNode1与htNode2被释放掉了,还是有一个拷贝的空间存在的,而这个空间存在于堆区,只能被手动释放,系统触碰不到的。