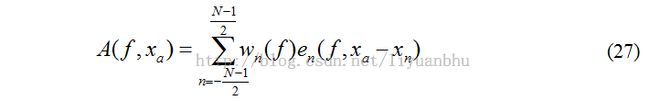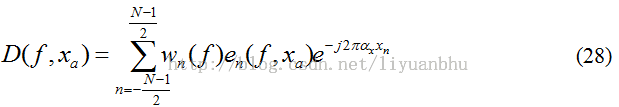麦克风阵列技术入门(3)
1.4. 离散传感器阵列
传感器阵列可以认为是对连续孔径的空间采样。每一个传感器可以看做是一个连续孔径。阵列的响应为所有传感器响应的叠加。
1.4.1. 一维传感器阵列
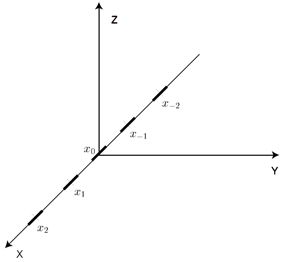
我们这里考虑一种特殊的一种最简单的离散传感器阵列,一维传感器阵列,传感器的数量为奇数,如图6所示。
图 6 离散麦克风阵列
每一个传感器的频率响应为en(f,x),传感器阵列的响应为每一个传感器响应的叠加。
在这里wn(f)是传感器的权重,xn 是第n个传感器在x轴上的位置。将这个式子带入公式15,可以得到远场的Directivity Pattern为:
如果所有的传感器都有相同的频率响应,那么孔径函数可以简化为:
相应的Directivity Pattern为:
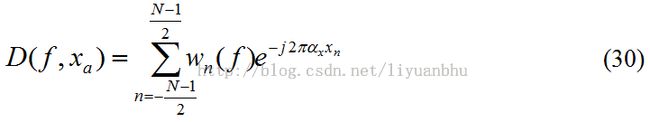
公式30给出了远场条件下具有N个传感器的一维线性传感器阵列的Directivity Pattern,当传感器等间距分布时,Directivity Pattern可以写为:
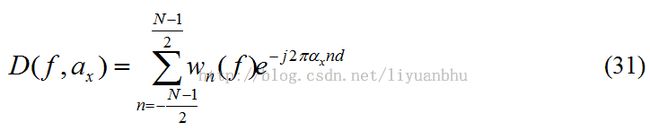
如果只考虑水平方向的Directivity Pattern,那么可以进一步写为:
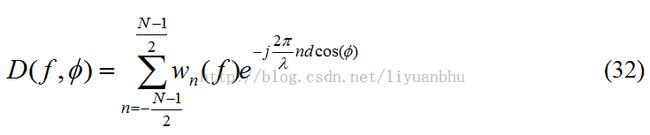
或者将上式中λ明确写为f的函数:

公式33给出了线性、等间距分布的麦克风阵列的Directivity Pattern,从这个公式中,我们可以看出Directivity Pattern取决于如下几个条件:
l 传感器的数量N
l 传感器间的间距d
l 声波的频率f
离散传感器阵列是连续孔径的一种近似。有一点需要注意的是,传感器阵列的有效长度定义为相应的连续孔径的长度,为L=Nd,而传感器阵列的实际长度是d(N-1)。
将Directivity Pattern画出,我们可以获得许多有用的信息。下面分三种情况画出图形。
1. 不同传感器数量。(L和f固定)
2. 不同的传感器阵列长度 L=Nd(N和f固定)
3. 不同的频率f(N和L固定)

图 7 不同传感器数量对应的Directivity Pattern(f=1KHz,L=0.5m)

图 8 不同的传感器阵列长度 L=Nd(N和f固定)

图 9 不同的频率,f 在400Hz到3000Hz之间(N和L固定)
从图7可以看出,随着空间采样频率的升高,sidelobe 逐渐减小。也就是说传感器用的越多,sidelobe 越小。图8可以看出,传感器阵列的长度越长,主峰的宽度越小。实际上,波束的宽度反比与fL,对于N 固定的场合,波束的宽度取决于fd。通常我们希望形成的波束的宽度固定,也就是要保证fd是固定的。图9给出了对于一个结构固定的麦克风阵列,形成的波束的宽度与信号频率之间的关系。