最小生成树之prime算法实现

prime算法的精髓在于：

每次选取一条边。

该边满足：1、一端已选，一端未选；2、该边权值最小。

直到选取n-1条边或选取n个顶点算法结束，求出MST或者判断出不存在MST。

 

代码设计：

1、利用两个集合存放已选顶点和未选顶点

（choosed[]存放已选顶点，unchoosed[]存放未选顶点）

2、每次选取的边都是一端在choosed[]中，另一端在unchoosed[]中的权值最小的边

3、利用STL中vector可以方便的实现图的临界表存储

4、记录组成MST的每条边很方便，只要在选取到一条满足条件的边时记录下起点、终点、权值即可

 

代码：

#include<iostream>
#include<cstring>
#include<vector>
using namespace std;

const int maxn=101;    //顶点数 
const int INF=0x7fffffff;

struct edge  //边 
{
    int to;    //到达的点 
    int cost;  //边的花费 
    bool flag; //是否入选 
};

int choosed[maxn];      //已选顶点 
int unchoosed[maxn];    //未选顶点 
int nodeNum,edgeNum,MST;  //顶点数、边数、最小生成树 
bool choose[maxn];     //顶点是否已选 
vector<edge> myV[maxn];  //图的邻接表 

/* 
  //这是无向图有重复边的建图，取重复边中最小的边存储 
bool exist(int from,int to,int cost)
{
    bool existFlag=false,smallFlag=false;
    
    for(int i=0;i<myV[from].size();i++)
    {
        if(myV[from][i].to==to)
        {
            existFlag=true;
            
            if(myV[from][i].cost>cost)
            {
                smallFlag=true;
                myV[from][i].cost=cost;
                break;
            }
        }
    }
    
    if(smallFlag)
    {
        for(int j=0;j<myV[to].size();j++)
        {
            if(myV[to][j].to==from)
            {
                myV[to][j].cost=cost;
                break;
            }
        }
    }
    
    if(existFlag) return true;
    return false;
}
             
void storeMap()   //邻接表存图 
{
    for(int j=0;j<maxn;j++)  //清空 
    {
        myV[j].clear();
    }
    
    memset(choose,false,sizeof(choose));  //标志图的各个点是否被选，不能重复 
    
    int from,to,cost,num=0;  //从from到to花费cost的边 
    
    for(int i=0;i<edgeNum;i++)
    {
        scanf("%d%d%d",&from,&to,&cost);
        
        //把图上的所有点不重复的放到unchoosed[]表中
        if(!choose[from])
        {
            unchoosed[num++]=from;
            choose[from]=true;
        }
        if(!choose[to])
        {
            unchoosed[num++]=to;
            choose[to]=true;
        }              
        
        if(!exist(from,to,cost))  //图中存在重复边的处理 
        {
            edge tmp;
            
            tmp.flag=false;
            tmp.cost=cost;
            
            //无向图 
            tmp.to=to;
            myV[from].push_back(tmp);
            
            tmp.to=from;
            myV[to].push_back(tmp);
        }
    }
}
*/
//无向图，无重复边的建图 
void storeMap()   //邻接表存图 
{
    for(int j=0;j<maxn;j++)  //清空 
    {
        myV[j].clear();
    }
    
    memset(choose,false,sizeof(choose));  //标志图的各个点是否被选，不能重复 
    
    int from,to,cost,num=0;  //从from到to花费cost的边 
    
    for(int i=0;i<edgeNum;i++)
    {
        scanf("%d%d%d",&from,&to,&cost);
        
        //把图上的所有点不重复的放到unchoosed[]表中
        if(!choose[from])
        {
            unchoosed[num++]=from;
            choose[from]=true;
        }
        if(!choose[to])
        {
            unchoosed[num++]=to;
            choose[to]=true;
        }              
        
        edge tmp;  
        tmp.flag=false;
        tmp.cost=cost;
            
        //无向图 
        tmp.to=to;
        myV[from].push_back(tmp);
            
        tmp.to=from;
        myV[to].push_back(tmp);
    }
}
 
void prime()  //prime算法 
{
    //初始化一些信息 
    MST=0;
    memset(choose,false,sizeof(choose));
    choosed[0]=unchoosed[0];
    choose[unchoosed[0]]=true;
    
    int choosedNum=1,from,to,cost,index;
    
    while(choosedNum<nodeNum)
    {
        cost=INF;
         
        //从所有已选顶点中，找一条费用最小，且没选的边 
        for(int i=0;i<choosedNum;i++)
        {
            for(int j=0;j<myV[choosed[i]].size();j++)
            {
                edge tmp=myV[choosed[i]][j]; 
                if(!choose[tmp.to] && !tmp.flag && tmp.cost<cost)
                {
                    from=choosed[i];
                    to=tmp.to;
                    cost=tmp.cost;
                    index=j; 
                }
            }
        }
         
        myV[from][index].flag=true;  //将找到的边标志为已选 
        
        //无向图，从from->to的边已选，那么从to->from的边也已选 
        for(int k=0;k<myV[to].size();k++)
        {
            if(myV[to][k].to==from)
            {
                myV[to][k].flag=true;
                break;
            }
        }
        
        choosed[choosedNum++]=to;  //将选择的顶点放到已选点集合中 
        choose[to]=true;
        
        MST+=cost;   //最小生成树费用增加 
    }
    
    printf("%d\n",MST);
}  
      
int main()
{
    while(scanf("%d%d",&nodeNum,&edgeNum)==2)  //输入图的点数、边数 
    {
        storeMap();         

        prime();
    }
    
    system("pause");
    return 0;
} 

 

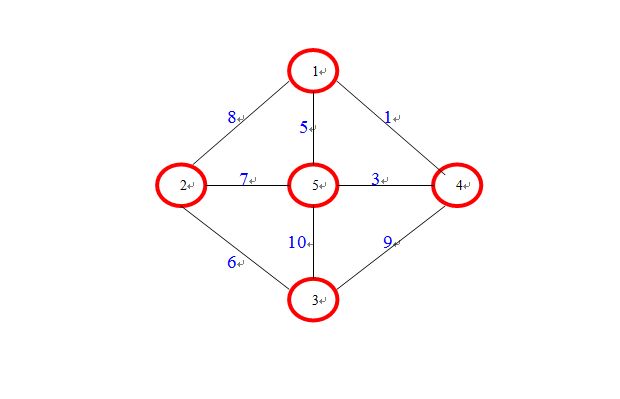
测试实例：

1、图形：

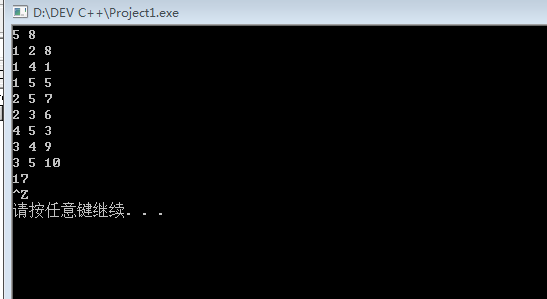
2、输入及结果：

 

问题：

如何利用prime算法求解有向图的MST？

先留在这吧。。。