STL set深入分析
其实写出一个set的程序很简单。但是这里面的东西可把我搞糊涂了一天，现在总算有点眉目了。写篇博客，希望后来者可以轻松的解决烦恼。
首先我们从set的构造函数开始，set<key,Compare&,Alloc>,第一个参数为元素类型，第二个为比较大小的，第三个为分配内存的。
元素类型我们可以是我们自己定义的类型，比较大小的函数也是可以我们自己定义的。至于内存分配，我们不用管，stl中有默认内存分配器。
为了从本质来分析set，我打算自己用自己定义的类型(一个结构体)，这样才有价值嘛。
struct Node
{
Node(int v=0,string s=" "):num(v),name(s){}
int num;
string name;
};
这就是我们的自定义类型。
但是set不知道怎么给我们的类型比较大小啊，不像int那些可以直接用。所以我们还欠缺一步就是写出比较元素大小的函数。
这里有两种方法：
方法一：(在自定义的结构体内定义)
struct Node
{
Node(int v=0,string s=" "):num(v),name(s){}
int num;
string name;
bool operator<(const Node& r) const
{
return strcmp(name.data(),r.name.data())<0;
}
};
这里是重载<，注意后面的const，至于函数体细节目前可以暂时不管。方法二：(在别的结构体内定义)
struct NodeLess
{
bool operator()(const Node& a,const Node& b) const
{
return strcmp(a.name.data(),b.name.data())<0;
}
};
这里是重载()，注意后面的const。
接下来来关注一下函数体的细节处理：
用于对关联容器排序的比较函数必须为它们所比较的对象定义一个‘严格的弱序化’(strick weak ordering)”。什么是严格的弱序化？让我们看看wiki上的定义：
严格弱序化拥有如下属性。对于集合S中所有的x，y，z，
对于所有的x，不存在x < x （非自反性 - 21条标题说的就是这个）
对于所有x不等于y，如果x < y那么不存在y < x （不对称性）
对于所有的x，y和z，如果x < y并且y < z，那么x < z（传递性）
如果x < y，那么对于所有的z，要么x < z要么z < y（或者两者都成立）
!cmp(key1,key2)&&!cmp(key2,key1)，如果key1==key2那么返回true,插入失败。
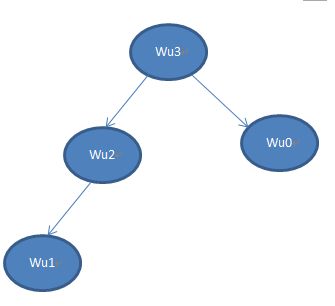
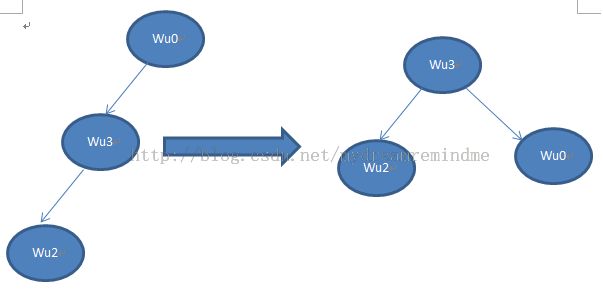
所以上面是return strcmp(name.data(),r.name.data())<0;而不仅仅是return strcmp(name.data(),r.name.data());因为并不能判定大小，而只是能判断是否是相同。让我们来分析一下吧。我们依次插入：Node(1,"wu0")，Node(4,"wu3")，Node(3,"wu2")，Node(2,"wu1")，Node(5,"wu4")，Node(5,"wu5")。
下面都是基于我用return strcmp(name.data(),r.name.data())来插入的。只是为了理解插入元素的思路。
====================》
===================================================================》
============================================》
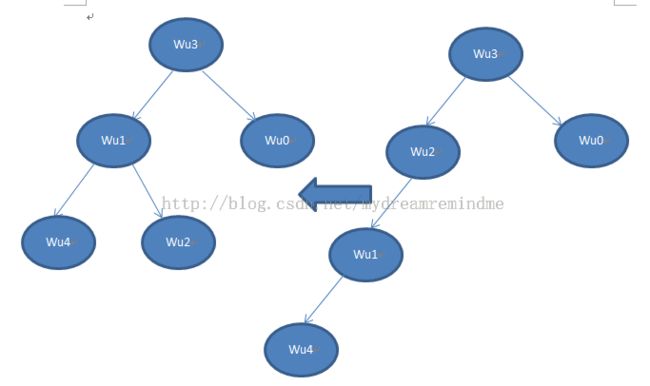
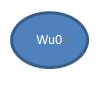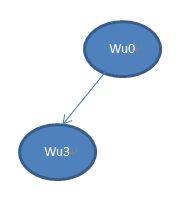这是根据红黑树来分析的，应该没错吧。。我也是临时看的红黑树。
通过分析，我们知道每次都是在节点的左边插入，因为每次返回的都是true,-1也是true啊，只有0才是false，而0是相等的元素的情况。所以我们应该要用return strcmp(name.data(),r.name.data())<0;以满足不对称性原则。
提供一个用法的例子吧。。
#include<iostream>
#include<string>
#include<set>
using namespace std;
struct Node
{
Node(int v=0,string s=" "):num(v),name(s){}
int num;
string name;
bool operator<(const Node& r) const
{
return strcmp(name.data(),r.name.data())<0;
}
};
void main()
{
set<Node>mySet;
set<Node>::iterator iter;
pair<set<Node>::iterator,bool> pairs;
pairs=mySet.insert(Node(1,"wu0"));
cout<<pairs.second<<endl;
pairs=mySet.insert(Node(4,"wu3"));
cout<<pairs.second<<endl;
pairs=mySet.insert(Node(3,"wu2"));
cout<<pairs.second<<endl;
pairs=mySet.insert(Node(2,"wu1"));
cout<<pairs.second<<endl;
pairs=mySet.insert(Node(5,"wu4"));
cout<<pairs.second<<endl;
pairs=mySet.insert(Node(5,"wu5"));
cout<<pairs.second<<endl;
pairs=mySet.insert(Node(4,"wu1"));
cout<<pairs.second<<endl;
for (iter = mySet.begin(); iter != mySet.end(); iter++)
cout<<(*iter).num<<" "<<(*iter).name<<endl;
iter=mySet.find(Node(3,"wu0"));
if(iter!=mySet.end())
cout<<((*iter).num)<<" "<<((*iter).name)<<endl;
else
cout<<"没找到"<<endl;
cout<<endl;
}
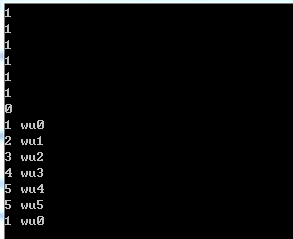
可以发现最后一个插入元素操作没有成功，因为set中已经有了一个wu1。
如果你还是用return strcmp(name.data(),r.name.data())来慢慢调试这个程序的话，可以得到很多东西，有兴趣的可以试试。