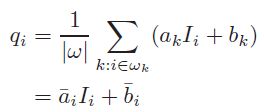引导滤波的opencv实现

from： http://blog.csdn.net/aichipmunk/article/details/21163543

引导滤波可以写出时间复杂度与窗口大小无关的算法，现在就来使用C++并借助OpenCV实现这一算法。

实现这种算法的关键思想是盒式滤波（box filter），而且必须是通过积分图来实现的盒式滤波，否则不可能与窗口大小无关，好在OpenCV的boxFilter函数满足这个要求。

再看看引导滤波的公式

先计算a_k的分子，Ip 在窗口w_k中的和，再除以窗口中像素的个数，刚好就是盒式滤波，因此我们可以将输入的引导图像 I 和滤波图像 p 相乘，并对相乘后的图像做box filtering，即得第一项的结果。后面的和分别为 I 和 p 在窗口w_k中均值，因此分别对 I 和 p 进行box filtering，再将box filtering之后的结果相乘即可。实际上，a_k的分子就是 Ip 在窗口w_k中的协方差。

接下来计算a_k的分母部分。是引导图 I 在窗口w_k中的方差，学过概率论与数理统计的朋友应该知道，方差和期望（均值）之间是有关系的，如下式

因此在计算 I 的方差时，我们可以先计算 I*I 的均值，再减去 I 均值的平方即的平方。在方法上，计算 I*I 的均值和计算 Ip 的均值是一样的。最后，对计算出来的方差图像，加上常量e（每个元素都加e），分母就计算完了，自然，a_k在所有窗口中的值也就得到了。b_k的计算太简单了，大家都懂的。

注意，我们的计算都是对整个图像的，以图像为单位进行计算，所以最后算出的也是两张图，a_k的图（左边）和b_k的图（右边），如下

在图中可以看到，在边缘部分或变化剧烈的部分，a的值接近于1（白色），b的值接近为0（黑色），而在变化平坦的区域，a的值接近0（黑色），b的值为平坦区域像素的均值。这与上一篇文章中所说的规律是一致的。

下面看第二个公式

输出值q又与两个均值有关，分别为a和b在窗口w_i中的均值（不是w_k），所以还是box filtering，我们将上一步得到两个图像都进行盒式滤波，得到两个新图：a_i和b_i，然后用a_i乘以引导图像 I ，再加上b_i，即得最终滤波之后的输出，如下（左边为原图，右边为滤波之后的图像，其中滤波窗口半径为8，e的值为500）：

下面是整个算法的代码，仅供参考

 void guidedFilter(Mat& source, Mat& guided_image, Mat& output, int radius, float epsilon)
 {
     CV_Assert(radius >= 2 && epsilon > 0);
     CV_Assert(source.data != NULL && source.channels() == 1);
     CV_Assert(guided_image.channels() == 1);
     CV_Assert(source.rows == guided_image.rows && source.cols == guided_image.cols);

     Mat guided;
     if (guided_image.data == source.data)
     {
         //make a copy
         guided_image.copyTo(guided);
     }
     else
     {
         guided = guided_image;
     }

     //将输入扩展为32位浮点型，以便以后做乘法
     Mat source_32f, guided_32f;
     makeDepth32f(source, source_32f);
     makeDepth32f(guided, guided_32f);

     //计算I*p和I*I
     Mat mat_Ip, mat_I2;
     multiply(guided_32f, source_32f, mat_Ip);
     multiply(guided_32f, guided_32f, mat_I2);

     //计算各种均值
     Mat mean_p, mean_I, mean_Ip, mean_I2;
     Size win_size(2*radius + 1, 2*radius + 1);
     boxFilter(source_32f, mean_p, CV_32F, win_size);
     boxFilter(guided_32f, mean_I, CV_32F, win_size);
     boxFilter(mat_Ip, mean_Ip, CV_32F, win_size);
     boxFilter(mat_I2, mean_I2, CV_32F, win_size);

     //计算Ip的协方差和I的方差
     Mat cov_Ip = mean_Ip - mean_I.mul(mean_p);
     Mat var_I = mean_I2 - mean_I.mul(mean_I);
     var_I += epsilon;

     //求a和b
     Mat a, b;
     divide(cov_Ip, var_I, a);
     b = mean_p - a.mul(mean_I);

     //对包含像素i的所有a、b做平均
     Mat mean_a, mean_b;
     boxFilter(a, mean_a, CV_32F, win_size);
     boxFilter(b, mean_b, CV_32F, win_size);

     //计算输出 (depth == CV_32F)
     output = mean_a.mul(guided_32f) + mean_b;
 }

 void makeDepth32f(Mat& source, Mat& output)
 {
     if (source.depth() != CV_32F ) > FLT_EPSILON)
         source.convertTo(output, CV_32F);
     else
         output = source;
 }