/*
poj3422 Kaka's Matrix Travels
题意:有个方阵,每个格子里都有一个非负数,从左上角走到右下角,每次走一步,只能往右或往下走,经过的数字拿走
每次都找可以拿到数字和最大的路径走,走k次,求最大和
这是 最大费用最大流 问题 每次spfa都找的是一条和最大的路径 s--到左上角的边流量是K限制增广次数
求最大费用最大流只需要把费用换成相反数,用最小费用最大流求解即可
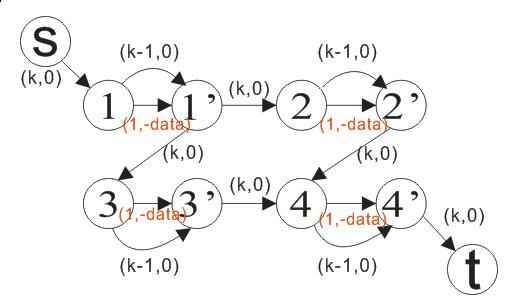
构图过程:如上图
每个点拆分成两个 a a' 之间建两条边(当然还要建退边),分别是 (费用为该点相反数,流量为1) (费用为0,流量为k-1)
路过这点时,可以通过前边那条边拿到数字,
以后再从这儿过,就没有数字可拿了,走的就是第二条边
然后是 没点向 右和下 建一条边 费用0,流量k
然后s、t连接左上角和右下角即可
求最小费用最大流的方法和EK求最大流的方法类似,
都是找一条增广路径,然后把流加进去
只不过EK找的是路径最短的增广路(广搜即可得)
而最小费用最大流 找的是费用最小的路径(对费用求最短路)
*/
#include<stdio.h>
#include<queue>
using namespace std;
struct node
{
int u,v,f,c,next;
}e[100000];
int n,k,head[5010],yong,s,t,maxflow;
int map[55][55];
int pre[5010],dist[5010],vis[5010];
void adde(int u,int v,int c,int f)//加边
{
e[yong].u=u,e[yong].v=v,e[yong].c=c,e[yong].f=f;
e[yong].next=head[u],head[u]=yong++;
e[yong].u=v,e[yong].v=u,e[yong].c=-c,e[yong].f=0;//这是它的退边
e[yong].next=head[v],head[v]=yong++;
}
int spfa()//spfa求最短路
{
int i,u,v;
for(i=0;i<=t;i++)
pre[i]=-1,vis[i]=0,dist[i]=0x7fffffff;
dist[s]=0;
vis[s]=1;
queue<int>q;
q.push(s);
while(!q.empty())
{
u=q.front();
q.pop();
for(i=head[u];i!=-1;i=e[i].next)
{
v=e[i].v;
if(e[i].f>0&&dist[u]+e[i].c<dist[v])
{
dist[v]=dist[u]+e[i].c;
pre[v]=i;//标记的是走到这儿的那条边
if(!vis[v])
{
vis[v]=1;
q.push(v);
}
}
}
vis[u]=0;
}
if(dist[t]==0x7fffffff)
return 0;
return 1;
}
int min(int a,int b){return a<b?a:b;}
void add()//加流 修改残留网络
{
int v;
int mm=0x7fffffff;
for(v=pre[t];e[v].u!=s;v=pre[e[v].u])//求最小的 可增流
mm=min(mm,e[v].f);
for(v=pre[t];e[v].u!=s;v=pre[e[v].u])
{
e[v].f-=mm;//修改残留网络
e[v^1].f+=mm;
maxflow+=mm*e[v].c;//加到费用里边
}
}
int main()
{
int i,j,b;
while(scanf("%d%d",&n,&k)!=EOF)
{
maxflow=0;//初始化
s=n*n*2;
t=s+1;
yong=0;
memset(head,-1,sizeof(head));
for(i=1;i<=n;i++)//读数据
for(j=1;j<=n;++j)
scanf("%d",&map[i][j]);
for(i=1;i<=n;i++)//拆点建边
for(j=1;j<=n;++j)
{
b=(i-1)*n+j-1;//点的编号是0~n*n-1
adde(b*2,b*2+1,-map[i][j],1);//
adde(b*2,b*2+1,0,k-1);
}
for(i=1;i<=n;i++)向右建边
for(j=1;j<n;j++)
{
b=(i-1)*n+j-1;
adde(b*2+1,2*(b+1),0,k);
}
for(i=1;i<n;++i)向下建边
for(j=1;j<=n;++j)
{
b=(i-1)*n+j-1;
adde(b*2+1,2*(b+n),0,k);
}
adde(s,0,0,k);//头
adde(n*n*2-1,t,0,k);//尾
while(spfa())
add();
printf("%d\n",-maxflow);//再取相反数
}
return 0;
}
