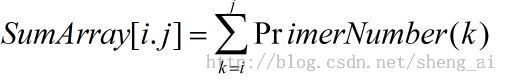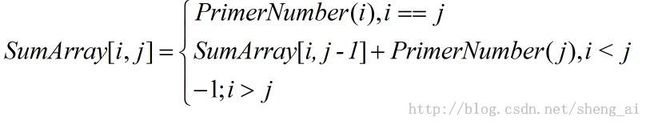POJ_2739

一.题目

Sum of Consecutive Prime Numbers

Time Limit: 1000MS

Memory Limit: 65536K

Description

Some positive integers can be represented by a sum of one or more consecutive prime numbers. How many such representations does a given positive integer have? For example, the integer 53 has two representations 5 + 7 + 11 + 13 + 17 and 53. The integer 41 has three representations 2+3+5+7+11+13, 11+13+17, and 41. The integer 3 has only one representation, which is 3. The integer 20 has no such representations. Note that summands must be consecutive prime 
numbers, so neither 7 + 13 nor 3 + 5 + 5 + 7 is a valid representation for the integer 20. 
Your mission is to write a program that reports the number of representations for the given positive integer.

Input

The input is a sequence of positive integers each in a separate line. The integers are between 2 and 10 000, inclusive. The end of the input is indicated by a zero.

Output

The output should be composed of lines each corresponding to an input line except the last zero. An output line includes the number of representations for the input integer as the sum of one or more consecutive prime numbers. No other characters should be inserted in the output.

Sample Input

2
3
17
41
20
666
12
53
0

Sample Output

1
1
2
3
0
0
1
2

二.解题技巧

     由于本题是给定一个整数，计算存在多少种将该整数分解为连续质数之和的方法，对于该问题，主要是解题思路类似于动态规划中的子串和问题，不同的是，这里是给定一个值，查找有多少个子串的和等于给定的值，可以参考动态规划来实现。

    主要解题思路是，由于给定的输入的范围为2-10000，因此，首先计算2-10000中的所有质数，存放在PrimerNumber中，然后，计算从第i个质数到第j个质数的和，将其保存在SumArray中，最后，根据输入的值的大小，在质数的和里面查找有多少个和与其相等，然后输出即可。

    如果只是单纯地按照上面的想法进行实现，有下面两个问题：  

    1.每次计算从第i个质数到第j个质数的和的时候，如果单纯地按照下面的式子进行计算的话，得到所有的从第i个到第j个质数的和的算法复杂度为。

    2.由于10000以内的只是的个数大约有1200多个，如果使用数组来表示从第i个质数到第j个质数的和的话，数组的大小大概为1200*1200，这样的实现会导致内存消耗特别大，我提交过一个这种实现的版本，内存消耗大概为6000多k，远远大于其他人提交的版本；

    对于问题1，利用动态规划的思想，可以将计算从第i个质数到第j个质数的计算公式转化为下面的形式：

    在转化为上述形式之后，就可以充分利用前面的计算结果，从而减少重复计算的次数，降低计算复杂度。

    对于问题2而言，按照问题1的解决方法，如果使用数组来保存第i个质数到第j个质数的和时，通过画图，可以知道，这个二维数组有一半的位置的值都为-1，同时，我们也可以发现，每一行真正有意义的值，都是从i==j位置开始的，也就是说，其实根据问题1的解决方法，对于每一个i的值是，当i==j时，可以直接得到质数和为该质数的值，当i<j是，可以根据公式计算得到，而且该计算公式并没有用到i>j的情况的结果，因此，在实现过程中，我们完全没有必要将i>j的情况的值保持下来，因此，不需要用二维数组来存储这些质数的值。

    为了便于实现，我们可以使用vector来存储质数的和，由于在i<j时，计算质数的和需要前面的一个计算的结果，因此，只需要使用一个变量将前面的结果保存下来即可，同时，考虑到输入的最大值为10000，因此，在计算完质数和之后，可以比较该质数和与10000的关系，如果该质数和已经大于10000了，则可以提前结束j的循环了。

三.实现代码

老版本（数组版本）

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

void MakePrimeNumber(vector<int>& PrimeNumbers, int Max)
{
    PrimeNumbers.clear();
    PrimeNumbers.push_back(2);

    for (int i = 3; i < Max; i = i + 2)
    {
        bool IsPrimer = true;
        if ( 0 == (i % 2))
        {
            IsPrimer = false;
        }

        for (int j = 3; j < i; j = j + 2)
        {
            if (i % j == 0)
            {
                IsPrimer = false;
                break;
            }
        }

        if (IsPrimer)
        {
            PrimeNumbers.push_back(i);
        }
    }


}


void MakeSum(const vector<int>& PrimeNumbers, int* SumArray)
{
    int Size = PrimeNumbers.size();
    for (int Index = 0; Index < Size; Index++)
    {
        for (int IndexJ = 0; IndexJ < Size; IndexJ++)
        {
            if (Index < IndexJ)
            {
                SumArray[Index * Size +IndexJ] =
                SumArray[Index * Size +IndexJ - 1] + PrimeNumbers[IndexJ];
            }
            if (Index > IndexJ)
            {
                SumArray[Index * Size + IndexJ] = -1;
            }
            if (Index == IndexJ)
            {
                SumArray[Index * Size + IndexJ] = PrimeNumbers[Index];
            }
        }
    }
}


int main()
{
    int Max = 10000;
    vector<int> PrimerNumbers;
    MakePrimeNumber(PrimerNumbers, Max);

    int Size = PrimerNumbers.size();
    int* SumArray = new int[Size * Size];
    MakeSum(PrimerNumbers, SumArray);

    int i = 0;
    int Result = 0;

    while(true)
    {
        cin >> i;
        if (i == 0)
        {
            break;
        }

        Result = count(SumArray, SumArray + Size * Size, i);
        cout << Result << endl;




    }

    delete[] SumArray;
    return 0;
}

新版本

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

void MakePrimeNumber(vector<int>& PrimeNumbers, int Max)
{
    PrimeNumbers.clear();
    PrimeNumbers.push_back(2);

    for (int i = 3; i < Max; i = i + 2)
    {
        bool IsPrimer = true;
        if ( 0 == (i % 2))
        {
            IsPrimer = false;
        }

        for (int j = 3; j < i; j = j + 2)
        {
            if (i % j == 0)
            {
                IsPrimer = false;
                break;
            }
        }

        if (IsPrimer)
        {
            PrimeNumbers.push_back(i);
        }
    }


}


void MakeSum(const vector<int>& PrimeNumbers, vector<int>& SumVec, int Max)
{
    SumVec.clear();
    int Size = PrimeNumbers.size();
    int PreValue = 0;
    for (int Index = 0; Index < Size; Index++)
    {
        for (int IndexJ = Index; IndexJ < Size; IndexJ++)
        {
            if (Index == IndexJ)
            {
                PreValue = PrimeNumbers[Index];
                SumVec.push_back(PreValue);
            }
            else
            {
                PreValue = PreValue + PrimeNumbers[IndexJ];

                if (PreValue > Max)
                {
                    break;
                }
                SumVec.push_back(PreValue);
            }
        }
    }
}


int main()
{
    int Max = 10000;
    vector<int> PrimerNumbers;
    MakePrimeNumber(PrimerNumbers, Max);

    vector<int> SumVec;
    MakeSum(PrimerNumbers, SumVec, Max);

    int i = 0;
    int Result = 0;

    while(true)
    {
        cin >> i;
        if (i == 0)
        {
            break;
        }

        Result = count(SumVec.begin(), SumVec.end(), i);
        cout << Result << endl;




    }

    return 0;
}

四.体会

    虽然这是一道比较水的题目，但是，里面也有些技巧，例如选择容器来保存质数和比单纯使用二维数组来保存质数和更加节省内存，以及对于i<j的情况的处理，同时，可以根据题目的限制，来减少保存的质数和的个数等。

版权所有，欢迎转载，转载请注明出处，谢谢