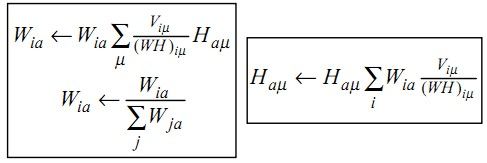Learning the parts of object by NMF

本文为Letters to nature上文章Learning the parts of objects by non-negativematrix factorization的读书笔记，针对如何基于NMF在神经网络中学习一个object的各层part做出理论上的分析，并在人脸part学习和text语义特征学习上做了相应实验。本文不含如何去解NMF，只给出非负约束下矩阵分解的结果。

 

Learning the parts of object by NMF

Rachel Zhang

 

1. Theoretical basis and Motivation

1. Part-based representation

    There is psychological and physiological evidence for parts-based representations in the brain, and certaincomputational theories of object recognition rely on such representations.

2. What is NMF? Why use NFM in NeuralNetwork?

    NMF: non-negative matrix factorization

    Difference: PCA, VQ learn holistic, not part-based representations, NMFdifferent from them via non-negative constrains.

    Virtue in Neural Network:

                1. Firing rates(number of spikes in a window) of neurons are nevernegative. 

                2. Synaptic strengths do not changesign.

 

 

2. Applied Experiments

3. Applied result of PCA, VQ and NMF

    Figure 1 shows the 3 methods learn to represent a face as a linearcombination of basis images.

    VQ: discovers a basisconsisting of whole-face prototypes.

    PCA: discovers a basis of ‘eigenfaces’,some of which resemble distorted versions of wholefaces.

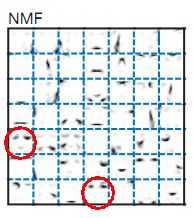
    NMF: discovers a basis consisting localized features that correspond better withintuitive notions of the parts of faces.

Figure 1.Basis of NMF, VQ and PCA

对于图中的encoding，红色表示负数，灰黑表示正数，颜色程度表示大小。

    

 

    4. Matrix Factorization framework

    为什么NMF会得出与PCA和VQ迥然不同的基呢？我们这里将这三种方法展示在Matrix factorizationframework里，首先看一下这个框架。图像数据库用n*m的矩阵V表示，每列包括m张人脸图中一张的n个非负像素值。这三种方法构造近似矩阵分解：V≈WH，or

V_iu≈(WH)_iu≈Σ_aW_iaH_au

    W∈R^n*r中的r列是basis images. H∈R^r*m中的每一列是编码，对应V中的一张脸。秩r的选择遵循(n+m)r<nm。下面说说VQ，PCA和NMF的区别。

 

    5. Difference in MF framework

    In VQ，each column in H is constrained to be a unary vector(一个非0元),也就是说每张脸只由一个基进行估计。PCA 在VQ的基础上做了松弛, it constrains the column of W to be orthonormal and the rows of H to beorthogonal to each other. 这样的松弛就允许了每张脸可以由一些基图像（即eigenface）通过线性组合生成了。尽管eigenfaces在统计上有最大variance的解释，但由于PCA对矩阵W和H的赋值是任意sign的，所以从视觉角度去想还不是很说得通。

     与一元向量约束的VQ不同，非负矩阵分解约束允许多个基图像组成一张人脸，但由于约束了W和H都非负，所以只允许增加基（不许减少）。所以基于NMF的方法可以构造出一个parts-based representation，这刚好符合了将不同parts组成一个整体的直觉想法。从图1中就可以看出，NMF的基和编码包含了一个大片0系数，或者说basis和encoding都是稀疏的。Basis的稀疏性源于基是局部信息（嘴巴、鼻子和其他人脸部分）在不同位置、形态的版本；由于不同人脸对这些versionsof faces’ parts 进行了组合、重用，所以encoding也是稀疏的，这和unaryencoding的VQ与fully distributed PCA都有很大不同。

 

    6. NMF的优化函数

    NMF优化目标函数：

该函数中，V_iu表示一个pixel，它由加入泊松噪声的（WH）_iu而得。因此目标函数实际上表示由基W和编码H产生图像V的概率。通过update算法，F将达到一个局部极大值。关于update的具体说明请见[2,3].

Figure 3. Iterativeupdate algorithm for NMF

图3中为updata算法，其单调收敛可以通过类似EM算法的收敛证明。更新算法保证了W和H的非负性及正交性（和W的标准正则性）。

 

 

    7. image pixels和编码变量的依赖关系：

    

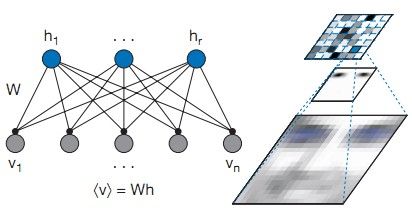
Figure 4. Probabilistichidden variables model underlying NMF

图4这个网络描述了底层可见变量Vi如何由生成高层隐变量生成。根据这个模型，V_i由Σ_aW_iaH_a生成。或者说H_a对V_i的影响可以用权值W_ia表示。在人脸图像应用中（右图），Vi就是V的第i列像素（底层的一个单元），隐变量（顶层）H_a(H的第a列)为第a个part-based基图像（中层，如某特定形态的眼睛）的编码. 给定a，W_1a…W_na就构成了一个特定basis image(中层)，和其他basis images一起构成了一个完整的人脸图像。

PS：[1]illustrate the versatility of NMF by applying NMF to the semantic analysis oftext documents. Refer to [1] ,P3, left part.

    

3. Method Analysis

8. 用NMF处理复杂问题<重点分析>

     尽管NMF在人脸识别和语义topic分析中比较成功，但这不表示它可以用于任何数据，比如采集到非固定点拍摄的图像，或者高清晰物体就不适合用NMF做。对于这种复杂问题part学习的处理，就需要一个多层隐变量的结构模型(类似DL)，而不像NMF中只用一层表示隐变量。另外，尽管非负这个约束可以进行part-based representation的学习，它们在编码的相关性方面也是有不足的，NMF只约束了W和H的非负性（这是唯一先验，只要求满足这个），而没有考虑到对于该先验，H内部元素间的相关性。比如，第一列第5幅，跟第4列最后一幅，那两列是有重合的地方：眼睛。它们线性组合表达人脸的时候，h对应这两位置的码应该相互间“有所协调”，否则就“重复”了。但是NMF不考虑的那么复杂，简单起见，假设他们不相关了。考虑的话是更复杂，更完善的模型，已有不少工作就是在这样方向上的改进，包括sparse的|X|1，|X|0。

     需要注意的是，这样无相关性仅仅是先验的无相关性，在v=Wh的或min |v-Wh|约束下h内部还是相互影响，相互制约的。有人叫你用W表达一幅人脸，但他先不给你看到那幅人脸，人脸V=Wh，表达人脸的码只事先要求是非负的，没有其它要求。所以你知道了客户没有关心h内部元素相关性，在先验里头它们是相互独立的。然后，他把人脸给你了，要满足你写的约束，这里h内部要相互协调线性组合出V来，所以约束下（而非先验下）还是有相关性的。

     9. ICA

     ICA是PCA的变种，假设隐变量相互独立且非高斯分布。将ICA用于人脸图像学出来的基是整体的(类似PCA)。ICA的独立假设不适于part-basedrepresentation学习，因为很多部分可能会同时出现，假设h内部元素独立就不能表示比较复杂的相关性。

 

 

     10．神经科学上的应用总结

     1). The consequence of non-negative constraints is that synapses are either excitatory or inhibitory,but do not change sign.

     2). In neural science, the non-negativity of the hidden and visible variables corresponds to the physiological fact that firing rates of neurons cannot be negative.

     3). One-sided constraints on neural activity and synaptic strengths in the brain may be important for developing sparsely distributed, parts-based representations for perception.

      这里解释下第一条，在神经元产生的时候，excitatory为正，inhibitory为0（而不为负）。因为如果刺激成功，产生spike，否则正常波动firing=0。所以在非负约束下H要么>0要么=0，不改变sign，使得NMF适用于神经信号firing rate矩阵分解。

  

Appendix - Code: implemented in MATLAB

1. Gradient Descent. 这个代码是台湾大学林智仁老师写的。

 function [W,H] = nmf(V,Winit,Hinit,tol,timelimit,maxiter)

 % NMF by alternative non-negative least squares using projected gradients
 % Author: Chih-Jen Lin, National Taiwan University

 % W,H: output solution
 % Winit,Hinit: initial solution
 % tol: tolerance for a relative stopping condition
 % timelimit, maxiter: limit of time and iterations

 W = Winit; H = Hinit; initt = cputime;

 gradW = W*(H*H') - V*H'; gradH = (W'*W)*H - W'*V;
 initgrad = norm([gradW; gradH'],'fro');
 fprintf('Init gradient norm %f\n', initgrad);
 tolW = max(0.001,tol)*initgrad; tolH = tolW;

 for iter=1:maxiter,
   % stopping condition
   projnorm = norm([gradW(gradW<0 | W>0); gradH(gradH<0 | H>0)]);
   if projnorm < tol*initgrad | cputime-initt > timelimit,
     break;
   end

   [W,gradW,iterW] = nlssubprob(V',H',W',tolW,1000); W = W'; gradW = gradW';
   if iterW==1,
     tolW = 0.1 * tolW;
   end

   [H,gradH,iterH] = nlssubprob(V,W,H,tolH,1000);
   if iterH==1,
     tolH = 0.1 * tolH;
   end

   if rem(iter,10)==0, fprintf('.'); end
 end
 fprintf('\nIter = %d Final proj-grad norm %f\n', iter, projnorm);

 function [H,grad,iter] = nlssubprob(V,W,Hinit,tol,maxiter)

 % H, grad: output solution and gradient
 % iter: #iterations used
 % V, W: constant matrices
 % Hinit: initial solution
 % tol: stopping tolerance
 % maxiter: limit of iterations

 H = Hinit; WtV = W'*V; WtW = W'*W;

 alpha = 1; beta = 0.1;
 for iter=1:maxiter,
   grad = WtW*H - WtV;
   projgrad = norm(grad(grad < 0 | H >0));
   if projgrad < tol,
     break
   end

   % search step size
   for inner_iter=1:20,
     Hn = max(H - alpha*grad, 0); d = Hn-H;
     gradd=sum(sum(grad.*d)); dQd = sum(sum((WtW*d).*d));
     suff_decr = 0.99*gradd + 0.5*dQd < 0;
     if inner_iter==1,
       decr_alpha = ~suff_decr; Hp = H;
     end
     if decr_alpha,
       if suff_decr,
     H = Hn; break;
       else
     alpha = alpha * beta;
       end
     else
       if ~suff_decr | Hp == Hn,
     H = Hp; break;
       else
     alpha = alpha/beta; Hp = Hn;
       end
     end
   end
 end

 if iter==maxiter,
   fprintf('Max iter in nlssubprob\n');
 end

2. Multiplier Update

multiplier update对应上面本文提到的更新方程。

 function [A, S] = nmf(X, K, type)
 NMF  Nonnegative Matrix Factorization.

 [A, S] = NMF(X, K, TYPE) performs nonnegative matrix factorization on the
 nonnegative M-by-N matrix X using K components. The M-by-K matrix A and
 the K-by-N matrix S are computed such that a divergence between X and A*S
 is minimized while preserving element-wise nonnegativity of both
 matrices.

 [A, S] = NMF(X, K, 'euc') uses the Euclidean distance.
 [A, S] = NMF(X, K, 'kl') uses the Kullback-Leibler divergence.
 [A, S] = NMF(X, K, 'is') uses the Itakura-Saito divergence.

 Author: Steve Tjoa
 Institution: University of Maryland (Signals and Information Group)
 Created: July 1, 2009
 Last modified: July 2, 2009

 This code was written during the workshop on Music Information Retrieval
 at the Center for Computer Research in Music and Acoustics (CCRMA) at
 Stanford University.

 Initialize parameters.
 maxiter = 100;
 [M, N] = size(X);
 O = ones(M, N);
 c = 1;  % safety parameter

 % Initialize outputs.
 A = rand(M, K);
 S = rand(K, N);

 if strcmp(type, 'euc')
     for iter=1:maxiter
         % Euclidean distance
         A = A.*(X*S' + c)./(A*(S*S') + c);
         S = S.*(A'*X + c)./((A'*A)*S + c);
         [A, S] = rescaledict(A, S);
     end

 elseif strcmp(type, 'kl')
     for iter=1:maxiter
         % KL Divergence
         A = A.*((X./(A*S))*S' + c)./(O*S' + c);
         S = S.*(A'*(X./(A*S)) + c)./(A'*O + c);
         [A, S] = rescaledict(A, S);
     end

 elseif strcmp(type, 'is')
     for iter=1:maxiter
         % IS Divergence
         A = A.*((X./(A*S).^2)*S' + c)./((1./(A*S))*S' + c);
         S = S.*(A'*(X./(A*S).^2) + c)./(A'*(1./(A*S)) + c);
         [A, S] = rescaledict(A, S);
     end
 end

 function [A, S] = rescaledict(A,S)
 % RESCALEDICT  Rescale dictionary.
 %
 % Author: Steve Tjoa
 % Institution: University of Maryland (Signals and Information Group)
 % Created: July 1, 2009
 % Last modified: July 2, 2009
 %
 % This code was written during the workshop on Music Information Retrieval
 % at the Center for Computer Research in Music and Acoustics (CCRMA) at
 % Stanford University.

 if nargin==2
     K = size(A,2);

     for k=1:K
         g = norm(A(:,k));
         A(:,k) = A(:,k)./g;
         S(k,:) = S(k,:).*g;
     end
 end
 end

 

    11. Reference

[1]. Daniel D.Lee* & H. Sebastian Seung* Learningthe parts of objects by Non-negative Matrix Factorization

[2]. Daniel D.Lee* & H. Sebastian Seung* Algorithms for Non-negative Matrix Factorization

[3]. Chih-Jen Lin On the Convergence of Multiplicative Update Algorithms for Non-negative Matrix Factorization

[4]. Phoyer U. NMF with sparse constraints. 论文中matlab代码实现 和 这只牛的主页。

本文尚不成熟，希望大家提出宝贵意见。

关于Machine Learning更多的学习资料与相关讨论将继续更新，敬请关注本博客和新浪微博Rachel____Zhang.

转自http://blog.csdn.net/abcjennifer/article/details/8579104