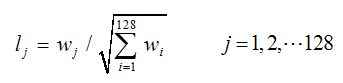从SIFT到SURF

1 SIFT

SIFT的原理详解见http://blog.csdn.net/zddblog/article/details/7521424（迄今为止，见过的SIFT最完全的原理推导和证明）

SIFT通俗易懂的证明和实现：http://blog.csdn.net/abcjennifer/article/details/7639681

Lindeberg等人在其尺度空间相关文献中证明尺度正则化的拉普拉斯高斯算子具有真正的尺度不变性，不过其需要计算二阶偏导数，而图像的高斯残差（Differnce ofGaussian）能够很好的对其进行近似。

       SIFT特征值提取出来之后同时具有2D、尺度、方向以及其局部矩形邻域的梯度信息。具体计算过程如下：

       （1）尺度空间极值点检测

       （2）关键点定位

       （3）关键点方向分配

       （4）关键点描述

       详细介绍如下：

       1、尺度空间极值点检测

       此处选用的尺度空间为高斯变尺度空间，L(x,y,sigma),通过sigma的变化来体现尺度的变化.而变尺度高斯函数与原始图像卷积得到图像为该尺度下的高斯模糊图像，即该图像在高斯变尺度空间下的图像。而不同尺度下的图像的差值即为DOG函数。为了保证尺度空间的连续性，通过缩放来实现整数级别的尺度变化，定义为一个变程域；在同一个组内通过高斯模糊来实现。

       1.1局部极值点检测

       局部极值是指在2D，尺度维度上相邻的26个点比较其是否为极值。

       1.2尺度域的取样频率

       试验确定

       1.3空间域的取样频率

       试验确定

       2、关键点精确定位

       在极值点（关键点候选点）进行DOG函数的Taylor展开，进行曲线逼近，对极值点的DOG值进行修正。

       2.1消除不稳定的边界相应

       DOG函数在图像边缘上有较大的相应，即便是该边缘点自身都不稳定，因此很容易受到噪声的影响。

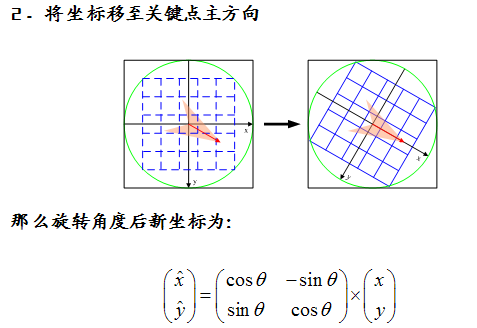
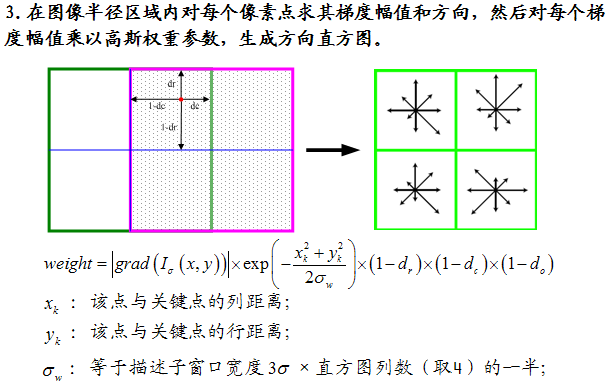
       3、为关键点分配方向

       根据关键点邻域内的梯度信息确定关键点的主方向。

       4、为关键点添加局部描述信息

总结SIFT思路：

1.       输入图像，建议做double(width*=2, height*=2, size*=4), 并高斯过滤进行平滑。

2.       由图片size决定建几个塔，每塔几层图像(一般3-5层)。0塔的第0层是原始图像(或你double后的图像)，往上每一层是对其下一层进行Laplacian变换（高斯卷积，其中sigma值渐大，例如可以是sigma, k*sigma, k*k*sigma…），直观上看来越往上图片越模糊。塔间的图片是降采样关系，例如1塔的第0层可以由0塔的第3层down sample得到，然后进行与0塔类似的高斯卷积操作。

3.       构建DoG金字塔。DoG金字塔由上一步生成的Gauss金字塔计算得到，塔数相同，每塔层数少1，因为DoG的每一层由Gauss的相邻两层相减得到。

4.       在DoG塔里进行极值点检测，并根据用户预设的对比度阈值、主曲率阈值去除不合法特征点。极值点检测用的Non-Maximal Suppression，即在3*3*3个点中进行灰度值比较，最小或最大才过关。

5.       计算每个特征点的尺度。注意塔间尺度关系，sigma*2.0^(octvs+intvl/intvls)

6.       计算每个特征点的梯度模值和方向。用特征点周围一个矩阵区域(patch)内的点来描述该特征点，用的直方图进行模值统计并寻找主方向，主方向可以不止一个。

7.       最后要生成64D或128D的特征描述符了。对齐主方向，计算方向直方图2D数组，假如每个直方图有8bin，那么64D(2*2*8bin)或128D(4*4*8bin)。

2 PCA-SIFT

PCA-SIFT (Principle Component Analysis), Y.ke, 2004

　•PCA-SIFT与标准SIFT有相同的亚像素位置，尺度和主方向。但在第4步计算描述子的设计，采用的主成分分析的技术。

　　•下面介绍一下其特征描述子计算的部分：

　　　　•用特征点周围的41×41的像斑计算它的主元，并用PCA-SIFT将原来的2×39×39维的向量降成20维，以达到更精确的表示方式。

　　　　•它的主要步骤为，对每一个关键点：在关键点周围提取一个41×41的像斑于给定的尺度，旋转到它的主方向 ；计算39×39水平和垂直的梯度，形成一个大小为3042的矢量；用预先计算好的投影矩阵n×3042与此矢量相乘；这样生成一个大小为n的PCA-SIFT描述子。

===============================

辅助资料：

3  SURF

SURF基于integral image，利用determination of Hessian matrix来描述极值点，也就是可能的特征点。

4 比较

共同点：

SIFT/SURF为了实现不同图像中相同场景的匹配，主要包括三个步骤：

1、尺度空间的建立；

2、特征点的提取；

3、利用特征点周围邻域的信息生成特征描述子

4、特征点匹配。

博客上看到一片文章，http://blog.csdn.net/cy513/archive/2009/08/05/4414352.aspx，这一段的大部分内容源于这篇文章，推荐大家去看看。

如果两幅图像中的物体一般只是旋转和缩放的关系，加上图像的亮度及对比度的不同，要在这些条件下要实现物体之间的匹配，SIFT算法的先驱及其发明者想到只要找到多于三对物体间的匹配点就可以通过射影几何的理论建立它们的一一对应。

如何找到这样的匹配点呢？SIFT/SURF作者的想法是首先找到图像中的一些“稳定点”，这些点是一些特殊的点，不会因为视角的改变、光照的变化、噪音的干扰而消失，比如角点、边缘点、暗区域的亮点以及亮区域的暗点。这样如果两幅图像中有相同的景物，那么这些稳定点就会在两幅图像的相同景物上同时出现，这样就能实现匹配。因此，SIFT/SURF算法的基础是稳定点。

SIFT/SURF提取的稳定点，首先都要求是局部极值。但是，当两个物体的大小比例不一样时，大图像的局部极值点在小图像的对应位置上有可能不是极值点。于是SIFT/SURF都采用图像金字塔的方法，每一个截面与原图像相似，这样两个金字塔中就有可能包含大小最近似的两个截面了。

这样找到的特征点会比较多，经过一些处理后滤掉一些相对不稳定的点。

接下来如何去匹配相同物体上对应的点呢？SIFT/SURF的作者都想到以特征点为中心，在周围邻域内统计特征，将特征附加到稳定点上，生成特征描述子。在遇到旋转的情况下，作者们都决定找出一个主方向，然后以这个方向为参考坐标进行后面的特征统计，就解决了旋转的问题。

 

共同的大问题有以下几个：

1、为什么选用高斯金字塔来作特征提取？

为什么是DOG的金字塔？因为它接近LOG，而LOG的极值点提供了最稳定的特征，而且DOG方便计算（只要做减法。）

为什么LOG的极值点提供的特征最稳定，有参考文献，未看。

 (7.12补充：)直观理解：特征明显的点经过不同尺度的高斯滤波器进行滤波后，差别较大，所以用到的是DOG。

但是直观上怎么理解？如果相邻Octave的sigma不是两倍关系还好理解：如果两幅图像只是缩放的关系，那么假设第一个Octave找到了小一倍图像的极值点，那么大一倍图像的极值点会在下一个Octave找到相似的。但是现在，如果把大一倍图像进行一次下采样（这样和小的图像就完全一样了），进行Gauss滤波时，两个图像滤波系数（sigma）是不一样的，不就找不到一样的极值点了么？不理解。

2、Hessian矩阵为什么能用来筛选极值点？

SIFT先利用非极大抑制，再用到Hessian矩阵进行滤除。SURF先用Hessian矩阵，再进行非极大抑制。SURF的顺序可以加快筛选速度么？（Hessian矩阵滤除的点更多？）

至于SURF先用Hessian矩阵，再进行非极大抑制的原因，是不管先极大值抑制还是判断Hessian矩阵的行列式，金字塔上的点的行列式都是要计算出来的。先判断是否大于0只要进行1次判断，而判断是否是极大值点或者极小值点要与周围26个点比较，只比较1次肯定快。

而在SIFT中，构建的高斯金字塔只有一座（不想SURF是有3座），要进行非极大抑制可以直接用金字塔的结果进行比较。而如果计算Hessian矩阵的行列式，还要再计算Dxx、Dxy、Dyy。因此先进行非极大抑制。这两个步骤的先后与SIFT/SURF的实际计算情况有关的，都是当前算法下的最佳顺序，而不是说哪种先计算一定更好。

3、为什么采用梯度特征作为局部不变特征？

这与人的视觉神经相关。采用梯度作为描述子的原因是，人的视觉皮层上的神经元对特定方向和空间频率的梯度相应很敏感，经过SIFT作者的一些实验验证，用梯度的方法进行匹配效果很好。

4、为什么可以采用某些特征点的局部不变特征进行整幅图像的匹配？

我在一份博客上找到这样一句话：（http://apps.hi.baidu.com/share/detail/32318290，大家可以看看这篇文章。）

从直观的人类视觉印象来看，人类视觉对物体的描述也是局部化的，基于局部不变特征的图像识别方法十分接近于人类视觉机理，通过局部化的特征组合，形成对目标物体的整体印象，这就为局部不变特征提取方法提供了生物学上的解释，因此局部不变特征也得到了广泛应用。

还有：

图像中的每个局部区域的重要性和影响范围并非同等重要，即特征不是同等显著的，其主要理论来源是Marr的计算机视觉理论和Treisman的特征整合理论，一般也称为“原子论”。该理论认为视觉的过程开始于对物体的特征性质和简单组成部分的分析，是从局部性质到大范围性质。

SIFT/SURF都是对特征点的局部区域的描述，这些特征点应该是影响重要的点，对这些点的分析更加重要。所以在局部不变特征的提取和描述时也遵循与人眼视觉注意选择原理相类似的机制，所以SIFT/SURF用于匹配有效果。

不同点的比较：

从博客上看到一个总结，我修改了一些内容。大家可以参看以下链接：

http://blog.csdn.net/ijuliet/archive/2009/10/07/4640624.aspx

SIFT	SURF
尺度空间	DOG与不同尺度的图片卷积	不同尺度的box filters与原图片卷积
特征点检测	先进行非极大抑制，再去除低对比度的点。再通过Hessian矩阵去除边缘的点	先利用Hessian矩阵确定候选点，然后进行非极大抑制
方向	在正方形区域内统计梯度的幅值的直方图，找max对应的方向。可以有多个方向。	在圆形区域内，计算各个扇形范围内x、y方向的haar小波响应，找模最大的扇形方向
特征描述子	16*16的采样点划分为4*4的区域，计算每个区域的采样点的梯度方向和幅值，统计成8bin直方图，一共4*4*8=128维	20*20s的区域划分为4*4的子区域，每个子区域找5*5个采样点，计算采样点的haar小波响应，记录∑dx, ∑dy,∑|dx|,∑|dy|，一共4*4*4=64维

SURF—金字塔仅仅是用来做特征点的检测。在计算描述子的时候，haar小波响应是计算在原图像（利用积分图）。而SIFT是计算在高斯金字塔上（注意不是高斯差分金字塔。）

性能的比较：

论文：A comparison of SIFT, PCA-SIFT and SURF  对三种方法给出了性能上的比较，源图片来源于Graffiti dataset，对原图像进行尺度、旋转、模糊、亮度变化、仿射变换等变化后，再与原图像进行匹配，统计匹配的效果。效果以可重复出现性为评价指标。

比较的结果如下：

method	Time	Scale	Rotation	Blur	Illumination	Affine
Sift	common	best	best	common	common	good
Pca-sift	good	good	good	best	good	best
Surf	best	common	common	good	best	good

 

 

 

 

 

 

由此可见，SIFT在尺度和旋转变换的情况下效果最好，SURF在亮度变化下匹配效果最好，在模糊方面优于SIFT，而尺度和旋转的变化不及SIFT，旋转不变上比SIFT差很多。速度上看，SURF是SIFT速度的3倍。

Luo Juan对这三种算法进行了实验比较，衡量参数有Processing time/ scale / changes/ rotation/ blur/ illumination/ affine，衡量指标有重复度或RANSAC内点概率，图片库来自这里。下面是大体赛况，您可以搜索"A comparison of SIFT, PCA-SIFT and SURF"看直播。

 

method	Time	Scale	Rotation	Blur	Illumination	Affine
Sift	common	best	best	common	common	good
PCA-sift	good	good	good	best	good	best
Surf	best	common	common	good	best	good

 

 

 

 

另外，SIFT、SURF也分别有了GPU实现，欢迎一起探讨学习！

SIFT on GPU, S.Heymann, 2005

SIFT on GPU(2), Sudipta N.Sinha, 2006

SURF on GPU, Nico Cornelis, 2008

 参考：http://blog.csdn.net/ijuliet/article/details/4640624

http://blog.csdn.net/abcjennifer/article/details/7639681

http://blog.csdn.net/cy513/article/details/4414352