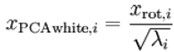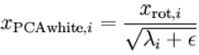PCA ,PCAWhitening ,ZCAWhitening
白化的目的:
举例来说,假设训练数据是图像,由于图像中相邻像素之间具有很强的相关性,所以用于训练时输入是冗余的。白化的目的就是降低输入的冗余性;更正式的说,我们希望通过白化过程使得学习算法的输入具有如下性质:(i)特征之间相关性较低;(ii)所有特征具有相同的方差
一、Pca白化 PcaWhitening
(1)消除数据的相关性
介绍的主成分分析Pca中,通过转化矩阵U,把原始数据映射到新的数据上;即Xrot=U*X;原始数据X经过转换后,得到的新的矩阵Xrot的各个维数的数据之间的相关性已经被消除;Xrot的协方差矩阵为对角阵,即表示其各个数据维度间无相关性;
(2)所有特征具有相同的方差
为了使每个输入特征具有单位方差,我们可以直接使用作为缩放因子来缩放每个特征。
白化后数据现在的协方差矩阵为单位矩阵 I。我们说白化是数据经过PCA后在缩放的版本;白化后数据中不同的特征之间不相关并且具有单位方差。
二、Zca白化,ZcaWhitening
最后要说明的是,使数据的协方差矩阵变为单位矩阵I的方式并不唯一。具体地,如果R是任意正交矩阵,即满足R*R'=I (说它正交不太严格, 可以是旋转或反射矩阵),那么经过R变换后的数据仍然具有单位协方差。在ZCA白化中,令R=U 。我们定义ZCA白化的结
果为:
![]()
可以证明,对所有可能的R,这种旋转使得Zca白化后的数据,尽可能地接近原始输入数据x。
三、正则化
实践中需要实现PCA白化或ZCA白化时,有时一些特征值在数值上接近于0,这样在缩放步骤时我们除以将导致除以一个接近0的值;这可能使数据上溢 (赋为大数值)或造成数值不稳定。因而在实践中,我们使用少量的正则化实现这个缩放过程,即在取平方根和倒数之前给特征值加上一个很小的常数:
当x在区间[-1,1]上时, 一般ε取值为 10-5。对图像来说, 这里加上ε,对输入图像也有一些平滑(或低通滤波)的作用。这样处理还能消除在图像的像素信息获取过程中产生的噪声,改善学习到的特征。
四:对图像应用主成分分析PCA on Images
为使PCA算法能有效工作,通常我们希望所有的特征都有相似的取值范围(并且均值接近于0)。如果你曾在其它应用中使用过PCA算法,你可能知道有必要单独对每个特征做预处理,即通过估算每个特征的均值和方差,而后将其取值范围规整化为零均值和单位方差。
在自然图像上进行训练时,对每一个像素单独估计均值和方差意义不大,因为(理论上)图像任一部分的统计性质都应该和其它部分相同,图像的这种特性被称作平稳性(stationarity)。具体而言,为使PCA算法正常工作,我们通常需要满足以下要求:
(1)特征的均值大致为0;
(2)不同特征的方差值彼此相似。
对于自然图片,即使不进行方差归一化操作,条件(2)也自然满足,故而我们不再进行任何方差归一化操作(对音频数据,如声谱,或文本数据,如词袋向量,我们通常也不进行方差归一化)。
实际上,PCA算法对输入数据具有缩放不变性,无论输入数据的值被如何放大(或缩小),返回的特征向量都不改变。更正式的说:如果将每个特征向量都乘以某个正数(即所有特征量被放大或缩小相同的倍数),PCA的输出特征向量都将不会发生变化。
既然我们不做方差归一化,唯一还需进行的规整化操作就是均值规整化,其目的是保证所有特征的均值都在0附近。根据应用,在大多数情况下,我们并不关注所输入图像的整体明亮程度。比如在对象识别任务中,图像的整体明亮程度并不会影响图像中存在的是什么物体。更为正式地说,我们对图像块的平均亮度值不感兴趣,所以可以减去这个值来进行均值规整化。
如果你处理的图像并非自然图像(比如,手写文字,或者白背景正中摆放单独物体),其他规整化操作就值得考虑了,而哪种做法最合适也取决于具体应用场合。但对自然图像而言,对每幅图像进行上述的零均值规整化,是默认而合理的处理。
PCA/Whitening部署
代码详解:
Step1:提取图片片段
x = sampleIMAGESRAW();![]()
%1000个样本图片片段,每个片段有144个特征维度。
[m n]=size(x);
x=x-repmat(mean(x,1),m,1);
%分别对每个样本进行0均值处理。
Step2:主成分计算
xRot = zeros(size(x));
sigma=x*x'/n; %计算协方差矩阵
[u s v]=svd(sigma);%矩阵的svd分解,u为一个正交矩阵(矩阵的行和列,线性无关),每一列为一个特征向量,s为特征值矩阵,v为另一个正交矩阵;由于此处sigma为对称的协方差矩阵(对称的方阵)。所以此处u和v互为转制,即u=v’;
xRot=u'*x; %数据的变化,变换后,xRot无相关性。
Step3:主成分计算检验
covar = zeros(size(x, 1));%covar为相关系数矩阵
covar = (1./m)*xRot*xRot';%计算相关系数矩阵
figure('name','Visualisation of covariance matrix');
imagesc(covar);%imagesc函数可以可视化相关系数矩阵,主对角线以外的矩阵区域为0,对应蓝色;主对角线上,为一套从上到下逐渐变暗的斜线;特征值逐渐减小
Step4:提取主成分
k = 0;
ss = diag(s);%把特征值矩阵,向量化
k = length(ss((cumsum(ss)/sum(ss))<=0.99));
注释:
%其中cumsum(ss)求出的是一个累积向量,也就是说ss向量值的累加值
>> a=[1 2 3 4 5];
>> cumsum(a)=1 3 6 10 15
%(cumsum(a)/sum(a))<=0.6 ;一个向量,值为0或者1的向量,为1表示该元素满足条件,值为0表示不满足这个条件。
>> (cumsum(a)/sum(a))<=0.6=1 1 1 0 0
>> b=a((cumsum(a)/sum(a))<=0.6)=1 2 3
xHat = zeros(size(x));
xHat = u*[u(:,1:k)'*x;zeros(m-k,n)]; %提取前k个主成分
Step5:PCAWhitening
epsilon = 0.1;%正则系数
xPCAWhite = zeros(size(x));
xPCAWhite = diag(1./sqrt(diag(s)+epsilon))*u'*x; %方差归一化
Step6:ZCAWhitening
xZCAWhite = u*xPCAWhite;
结果分析,源码:http://www.cnblogs.com/tornadomeet/archive/2013/03/22/2975456.html
Andrew ng 教程:http://deeplearning.stanford.edu/wiki/index.php/Exercise:PCA_and_Whitening