B-spline曲面的法线贴图

*原创文章，转载请注明出处*

 

B-spline曲面的法线贴图

Normal Mapping on B-spline Surface

 

在openGL Cg系列教程中，有一篇文章详细的介绍了法线贴图的原理和实现。这种法线贴图的实现是基于平面的，也就是最常看到的在四边形上的法线贴图。如果想在一些几何体上贴图，比如torus，我们可以利用torus的参数方程进行法线贴图。对于曲面，可以通过tessellation技术，将曲面用很多三角形网格来表示，然后再将三角形用两个参数s和t的参数方程来表示后，即可对该曲面进行法线贴图。对于B-spline曲面，这里介绍一种使用B-spline曲面方程来进行法线贴图的方法。

 

在这之前，有必要先来了解一下B-spline曲面。给定m+1行，每行n+1个控制点(control points)P_i,j，并且给定在u方向的h+1个knot序列U={u₀,u₁,…,u_h}，V方向上的k+1个knot序列V={v₀,v₁,…,v_k}，如果u方向的次数为p，v方向的次数q，那么该B-spline曲面S(u,v)的定义为：

 

 

 

这里N_i,p(u)表示p次第i个B-spline基函数(basis function)， N_j,q(v)表示q次第j个B-spline基函数。从B-spline公式中可以看出，B-spline曲面是由u方向上的B-spline曲线和v方向上的B-spline曲面的线性组合。关于B-spline基函数的定义，可以参考文章Introduction to B-Spline Curves。下面来看一个B-spline曲面的例子。

 

例：

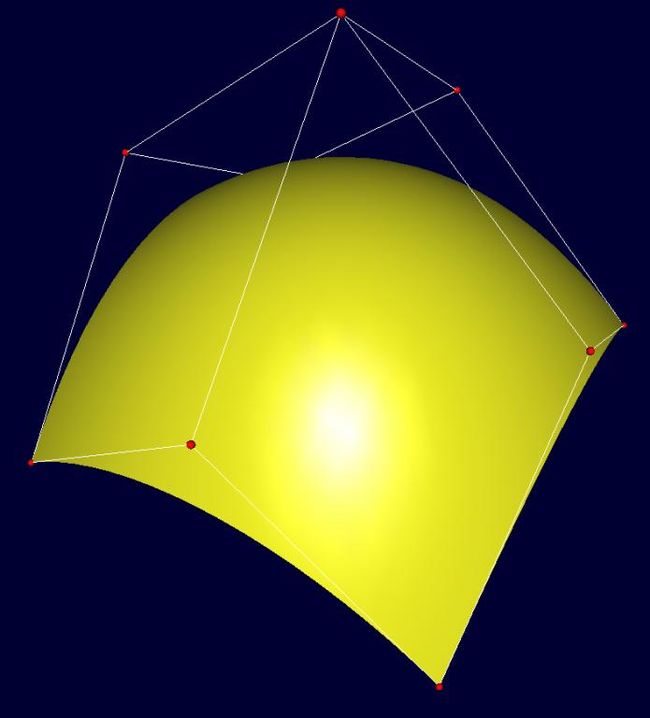
已知u方向knot序列U={0,0,0,1,1,1}，基函数次数p=2，v方向knot序列V={0,0,0,1,1,1}，基函数次数q=2，曲面的控制点为{(-10,0,-10),(0,10,-10),(10,0,-10),(-10,10,0),(0,20,0),(10,10,0),(-10,0,10),(0,10,10),(10,0,10)}。

 

 

Fig1 B-spline曲面

 

既然B-spline曲面公式中含有两个参数u和v，而参数的范围是可以任意指定的，只要满足

 

 

这个条件即可。如果将B-spline曲面的u和v方向的knot序列看作是参数空间，并将两个参数的范围都指定在0和1之间，我们完全可以让这个参数和纹理坐标对应。

 

 

Fig2 B-spline曲面参数空间和纹理坐标的对应

 

上图中显示了B-spline曲面参数和纹理坐标的对应关系。我们利用这种对应关系就可以在B-spline曲面上实现法线贴图。

 

在介绍法线贴图的那篇教程中提到过，要将法线贴图应用到任意物体的表面，光照计算必须在纹理空间中进行，这就要求计算出物体顶点的Frenet Frame，然后将该坐标系作为纹理坐标系来计算。Frenet Frame是由顶点切向量T，法向量N和第二法向量B组成的坐标系。

 

F = [ T N B ]

 

下面来看看怎样计算B-spline曲面的纹理坐标系。上面已经提到，在B-spline曲面的参数空间中有两个方向u和v，那么我们就可以分别在这两个方向上求偏导数，

 

 

这个公式表示曲面S(u,v)的k+l阶偏导数等于曲面对u求k阶偏导数然后再对v求l阶偏导数。和分别表示B-spline基函数的k阶导数和l阶导数。为了构造纹理坐标系，只需要1阶偏导数就足够了，于是上面的公式可以写为：

 

 

 

这里

 

 

 

现在我们需要分别在u和v方向上的偏导数

 

 

求出曲面u和v方向上的偏导数后，于是可以像下面一样构建纹理坐标系

 

 

 

 

很明显，这里纹理坐标系是由曲面u方向一阶导数和v方向一阶导数所组成，其中的乘号表示向量的外积。在Fig3中可以看到B-spline曲面上每个顶点的纹理坐标系，红色线表示u方向一阶导数，蓝色线表示v方向一阶导数，绿色线表示它们的外积。

 

 

Fig3 B-spline曲面上顶点的纹理坐标

 

一旦构建好纹理坐标后，光照的计算都转换到该坐标下计算即可。下面是B-spline曲面使用法线贴图的例子。

 

(a)

(b)

 

Fig4 B-spline曲面上的法线贴图

 

Fig4(a)和(b)可以看出光源在不同位置时，法线贴图的效果。Fig4中只使用了diffuse和法线贴图合成的效果，当然我们也可以用纹理和法线贴图合成，如下面的Fig5。

 

(a)

(b)

Fig5 B-spline 

 

 

 

 

曲面上的法线贴图和纹理贴图

*原创文章，转载请注明出处*