红黑树代码

为了能更好的理解红黑树，我把我写的关于红黑树代码放在博客里，如果有什么问题，欢迎大家留言，谢谢

 定义一个结点部分

enum COLOR{RED, BLACK};

class CRB_Node
{
	

public:
	CRB_Node(void);
	CRB_Node(const int item, CRB_Node * lch,CRB_Node * rch, CRB_Node *par );
	~CRB_Node(void);

	friend ostream& operator<<(ostream &output, const CRB_Node & node);
	friend ostream& operator<<(ostream &output, const COLOR & color);
public:
	COLOR RB_COLOR;
	CRB_Node *left;
	CRB_Node *right;
	CRB_Node *parent;
	int key;

};
CRB_Node::CRB_Node(void)
{
	RB_COLOR = BLACK;
	right = NULL;
	left = NULL;
	parent = NULL;
	key = -1;	//-1代表是空节点
}

CRB_Node::CRB_Node(const int item, CRB_Node * lch,CRB_Node * rch, CRB_Node *par )
{
	RB_COLOR = RED;
	right = rch;
	left = lch;
	parent = par;
	key = item;
}

CRB_Node::~CRB_Node(void)
{
}

	//这个重载必须放在.cpp中
ostream& operator<<(ostream &output, const CRB_Node & node)
{

	output<<node.key<<node.RB_COLOR<<",";

	return output;
}


ostream& operator<<(ostream &output, const COLOR & color)
{
	if ( color == RED )
	{
		output<<"(红)";
	}
	else 
	{
		output<<"(黑)";
	}
	return output;
}

红黑树的类操作

class CRB_Tree
{
public:
	CRB_Tree(void);
	~CRB_Tree(void);

	void CreateRBT(void);
	bool Insert(const int item);
	bool IsEmpty(void);		//判断是否为空
	CRB_Node* Find(const int item);		//查找关键字item
	void OutPut(void);
	bool Delete();
	int GetHeight();

	CRB_Node* InOrderSuccessor(CRB_Node* pNode);

public:		//内部调用
	int _Height(CRB_Node *pNode);
	void _DeleteFixUp(CRB_Node * pNode);
	void  _rbInsertFixUp(CRB_Node * pInsertNode);
	void _leftRotate(CRB_Node * pNode);
	void _rightRotate(CRB_Node * pNode);


public:
	CRB_Node * m_pRoot;
	CRB_Node * m_pNullNode;		//记录一个空指针,将树中的空指针都直到这个位置
}；
CRB_Tree::CRB_Tree(void)
{
	m_pNullNode = new CRB_Node();
	m_pRoot = m_pNullNode;

}

CRB_Tree::~CRB_Tree(void)
{
	delete m_pNullNode;
}

bool CRB_Tree::IsEmpty(void)
{
	if ( m_pRoot == m_pNullNode )
	{
		return true;
	}
	else
	{
		return false;
	}
}

void CRB_Tree::CreateRBT(void)
{
	cout<<"请输入数字(-1结束)："<<endl;
	int item = 0;
	while ( cin>>item && item != -1 )
	{
		Insert(item);
	}
}

bool CRB_Tree::Insert(const int item)
{
	CRB_Node * t = m_pRoot; 
	CRB_Node * pInsertNode = new CRB_Node(item, m_pNullNode, m_pNullNode, m_pNullNode);	//要插入的节点,初始化
	CRB_Node * pInsertParent = m_pNullNode;	//记录父亲节点

	while ( t != m_pNullNode )
	{
		pInsertParent = t;
		if ( t->key > item )
		{
			t = t->left;
		}
		else if ( t->key < item )
		{
			t = t->right;
		}
		else
		{
			return false;	//树中找到相等的节点，则插入失败
		}
	}
	
	pInsertNode->parent = pInsertParent;	//插入节点的父亲赋值

	if ( pInsertParent == m_pNullNode )		//树为空
	{
		m_pRoot = pInsertNode;
	}
	else if ( item < pInsertParent->key )
	{
		pInsertParent->left = pInsertNode;
	}
	else
	{
		pInsertParent->right = pInsertNode;
	}
	_rbInsertFixUp( pInsertNode );	//调整树，使它满足红黑树的性质
	return true;
}

void CRB_Tree::_rbInsertFixUp( CRB_Node * pInsertNode)
{
	CRB_Node * pUncleNode = m_pNullNode;	//插入节点的叔叔，初始化

	//插入节点的父节点如果是黑色，则无需处理满足性质，只有当父节点是红色时，才处理 
	while ( pInsertNode->parent->RB_COLOR == RED )
	{
		if ( pInsertNode->parent == pInsertNode->parent->parent->left )	//如果插入节点的父亲是插入节点的祖父的左子树
		{
			pUncleNode = pInsertNode->parent->parent->right;	//叔叔为祖父的右子树
			if ( pUncleNode->RB_COLOR == RED )	//插入节点的叔叔也是红色
			{
				pInsertNode->parent->RB_COLOR = BLACK;
				pUncleNode->RB_COLOR = BLACK;
				pUncleNode->parent->RB_COLOR = RED;
				pInsertNode =  pInsertNode->parent->parent ;	//当前处理节点变为祖父节点
			}
			else if (pInsertNode == pInsertNode->parent->right)	//插入节点的叔叔是黑色，且为祖父的右子树,且插入节点为父节点的右子树
			{
				pInsertNode = pInsertNode->parent;
				_leftRotate(pInsertNode);	//以当前节点为跟，进行左枝旋转				
			}
			else if (pInsertNode == pInsertNode->parent->left)	//插入节点的叔叔是黑色，且为祖父的右子树，且插入节点为父节点的左子树
			{
				pInsertNode->parent->RB_COLOR = BLACK;
				pInsertNode->parent->parent->RB_COLOR = RED;
				_rightRotate(pInsertNode->parent->parent);	//以当前接节点为跟，进行右枝旋转；
			}
		}
		else	//如果插入节点的父亲是插入节点的祖父的右子树
		{
			pUncleNode = pInsertNode->parent->parent->left;	//插入节点的叔叔为祖父的左子树
			if ( pUncleNode->RB_COLOR == RED )
			{
				pInsertNode->parent->RB_COLOR = BLACK;
				pUncleNode->RB_COLOR = BLACK;
				pUncleNode->parent->RB_COLOR = RED;
				pInsertNode = pInsertNode->parent->parent;
			}
			else if (pInsertNode == pInsertNode->parent->right)	//插入节点的叔叔是黑色，且为左子树,且插入节点为父节点的右子树
			{
				pInsertNode->parent->RB_COLOR = BLACK;
				pInsertNode->parent->parent->RB_COLOR = RED;
				_leftRotate(pInsertNode->parent->parent);	//以当前节点为跟，进行作旋转
			}
			else if (pInsertNode == pInsertNode->parent->left )	//插入节点的叔叔是黑色，且为左子树，且插入节点为父节点的左子树
			{
				pInsertNode = pInsertNode->parent;
				_rightRotate(pInsertNode);	//以当前节点为跟，进行右旋转
			}
		}
	}
	
	m_pRoot->RB_COLOR = BLACK;	//将跟变成黑色, Case1情况
}

void CRB_Tree::_rightRotate(CRB_Node * pNode)
{
	if ( pNode == m_pNullNode || pNode->left == m_pNullNode )
	{
		return;
	}
	CRB_Node * pTempL = pNode->left;

	pNode->left = pTempL->right;
	pTempL->parent = pNode->parent;

	//当pTempL->right不为空时，其父亲指向pNode
	if ( pTempL->right != m_pNullNode )
	{
		pTempL->right->parent = pNode;
	}

	if ( pNode->parent == m_pNullNode )
	{
		m_pRoot = pTempL;
	}
	else
	{
		if ( pNode == pNode->parent->right )//当前pNode为父亲的右子树
		{
			pNode->parent->right = pTempL;
		}
		else
		{
			pNode->parent->left = pTempL;
		}
	}
	pNode->parent = pTempL;
	pTempL->right = pNode;
}

void CRB_Tree::_leftRotate(CRB_Node * pNode)
{
	if ( pNode == m_pNullNode || pNode->right == m_pNullNode )
	{
		return ;	//无法旋转

	}
	CRB_Node * pTempR = pNode->right;
	pNode->right = pTempR->left;
	
	pTempR->parent = pNode->parent;
	//如果当前节点的右子树的左子树不为空，则将其父亲指向当前节点
	if ( pTempR->left != m_pNullNode )
	{
		pTempR->left->parent = pNode;
	}

	//如果当前节点的父亲为空
	if ( pNode->parent == m_pNullNode )
	{
		m_pRoot = pTempR;
	}
	else
	{
		if ( pNode == pNode->parent->left )	//当前节点为父亲左子树
		{
			pNode->parent->left = pTempR;
		}
		else	//当前节点为父亲的右子树
		{
			pNode->parent->right = pTempR;
		}
	}
	pNode->parent = pTempR;
	pTempR->left = pNode;
}

void CRB_Tree::OutPut(void)
{
	CRB_Node * pTemp = NULL;
	list<CRB_Node*> gList;
	gList.push_back(m_pRoot);
	int cur = 0;
	int last = 1;

	cout<<endl<<"树的形状为："<<endl;

	while ( cur < (int)gList.size() )
	{
		last = gList.size();
		while ( cur < last )
		{
			pTemp = *gList.begin();
			gList.pop_front();
			cout<<*pTemp;
			if ( pTemp->key != -1)
			{
				if ( pTemp->left )
				{
					gList.push_back(pTemp->left);
				}
				else	//如果不存在左子树，则插入一个特殊节点
				{
					CRB_Node * pTemp1 = new CRB_Node();
					gList.push_back(pTemp1);
				}
				if ( pTemp->right )
				{
					gList.push_back(pTemp->right);
				}
				else	//如果不存在右子树，则插入一个特殊节点
				{
					CRB_Node * pTemp2 = new CRB_Node();
					gList.push_back(pTemp2);
				}
			}

			cur++;
		}	
		cout<<endl;	//一行结束，换行
		cur = 0;
	}
}

CRB_Node* CRB_Tree::Find(const int item)
{
	CRB_Node * pTemp = m_pRoot;
	while ( pTemp != m_pNullNode )
	{
		if ( pTemp->key == item )
		{
			return pTemp;
		}
		else if ( pTemp->key > item )
		{
			pTemp = pTemp->left;
		}
		else 
		{
			pTemp = pTemp->right;
		}
	}

	return pTemp;	//找不到时，返回指向空节点
}

bool CRB_Tree::Delete()
{
	int item = -1;
	cout<<endl<<"请输入要删除的数：";
	cin>>item;

	if ( item == -1 )
	{
		return false;	//没有找到要删除的结点
	}

	CRB_Node * pDelPoint = Find(item);

	if ( pDelPoint == m_pNullNode )
	{
		cout<<"没有找到要删除结点"<<endl;
		return false;	//没有找到要删除的节点
	}

	//删除节点的左右子树均非空
	if ( pDelPoint->left != m_pNullNode && pDelPoint->right != m_pNullNode )
	{
		//找到要删除节点的后继节点
		CRB_Node * successor = InOrderSuccessor(pDelPoint);
		pDelPoint->key = successor->key;
		
		pDelPoint = successor;
	}

	CRB_Node * pDelPointChild = NULL;	//记录删除节点的孩子节点，先右后左
	if ( pDelPoint->right != m_pNullNode )
	{
		pDelPointChild = pDelPoint->right;
	}
	else if (pDelPoint->left != m_pNullNode )
	{
		pDelPointChild = pDelPoint->left;
	}
	else
	{
		pDelPointChild = m_pNullNode;
	}

	pDelPointChild->parent = pDelPoint->parent;
	if ( pDelPoint->parent == m_pNullNode )	//如果删除的是根节点
	{
		m_pRoot = pDelPointChild;
	}
	else if ( pDelPoint == pDelPoint->parent->right )
	{
		pDelPoint->parent->right = pDelPointChild;
	}
	else
	{
		pDelPoint->parent->left = pDelPointChild;
	}
	//如果删除的黑节点，且删除的结点孩子和父亲至少有一个不为空
	if ( pDelPoint->RB_COLOR == BLACK && 
		!(pDelPointChild == m_pNullNode && pDelPointChild->parent == m_pNullNode) )
	{
		_DeleteFixUp(pDelPointChild);
	}
	delete pDelPoint;
	return true;
}

CRB_Node* CRB_Tree::InOrderSuccessor(CRB_Node *pNode)
{
	//如果pNode 是空节点
	if ( pNode == m_pNullNode )
	{
		return m_pNullNode;
	}

	//找直接后继
	CRB_Node* pResult = pNode->right;
	while ( pResult != m_pNullNode )
	{
		if ( pResult->left != m_pNullNode )
		{
			pResult = pResult->left;
		}
		else
		{
			break;
		}
	}

	//如果删除节点的右子树为空
	if ( pResult == m_pNullNode )
	{
		CRB_Node* pIndex = pNode->parent;
		pResult = pNode;
		//要删除节点是其父亲的左子树，父亲不为空
		while ( pIndex != m_pNullNode && pResult == pIndex->right )
		{
			pResult = pIndex;
			pIndex = pIndex->parent;
		}
		pResult = pIndex;
	}
	return pResult;
}

void CRB_Tree::_DeleteFixUp(CRB_Node *pNode)
{
	//如果删除节点不是跟，且删除节点是黑节点
	while ( pNode != m_pRoot && pNode->RB_COLOR == BLACK )
	{
		//如果删除节点是父亲的左子树
		if ( pNode == pNode->parent->left )
		{
			//兄弟是右子树
			CRB_Node* pBrother = pNode->parent->right;
			if ( pBrother->RB_COLOR == RED )
			{
				pBrother->RB_COLOR = BLACK;
				pNode->parent->RB_COLOR = RED;
				_leftRotate(pNode->parent);
			}
			else
			{
				//兄弟结点为黑色
				//兄弟左右子树都为黑色
				if (pBrother->left->RB_COLOR == BLACK && pBrother->right->RB_COLOR == BLACK )
				{
					pBrother->RB_COLOR = RED;
					pNode = pNode->parent;
				}
				else if ( pBrother->right->RB_COLOR == BLACK )	//兄弟的左子树为红，右子树为黑
				{												//操作:兄弟变红，兄弟左子树变黑		兄弟左旋
					pBrother->left->RB_COLOR = pBrother->parent->RB_COLOR;	//左侄变兄弟父亲颜色
					pBrother->parent->RB_COLOR = BLACK;		//父亲边黑色
					_rightRotate(pBrother);		//兄弟右旋
					_leftRotate(pNode->parent);		//父亲左旋
				}
				else if ( pBrother->right->RB_COLOR == RED )	//兄弟的右子树为红，
				{												//兄弟变父色，父亲边黑色，兄弟右子树变黑	父亲左旋
					pBrother->RB_COLOR = pBrother->parent->RB_COLOR;
					pBrother->parent->RB_COLOR = BLACK;
					pBrother->right->RB_COLOR = BLACK;
					_leftRotate(pBrother->parent);
					pNode = m_pRoot;
				}
			}
		}
		else	//删除节点为父亲的右子树
		{
			CRB_Node* pBrother = pNode->parent->left;
			if ( pBrother->RB_COLOR == RED )
			{
				pBrother->RB_COLOR = BLACK;
				pNode->parent->RB_COLOR = RED;
				_rightRotate(pNode->parent);
			}
			else	//如果兄弟为黑色
			{
				if ( pBrother->left->RB_COLOR == BLACK && pBrother->right->RB_COLOR == BLACK )
				{
					pBrother->RB_COLOR = RED;
					pNode = pNode->parent;
				}
				else if ( pBrother->left->RB_COLOR == BLACK	)	//兄弟的左子树为黑,右子树为红
				{
					pBrother->right->RB_COLOR = pBrother->parent->RB_COLOR;	//左侄变兄弟父亲颜色
					pBrother->parent->RB_COLOR = BLACK;		//父亲边黑色
					_leftRotate(pBrother);		//兄弟右旋
					_rightRotate(pNode->parent);		//父亲左旋
				}
				else if ( pBrother->left->RB_COLOR == RED )		//兄弟的左子树为红色
				{
					pBrother->RB_COLOR = pBrother->parent->RB_COLOR;
					pBrother->parent->RB_COLOR = BLACK;
					pBrother->left->RB_COLOR = BLACK;
					_rightRotate(pBrother->parent);
					pNode = m_pRoot;
				}
			}
		}
	}

	pNode->RB_COLOR = BLACK;
}

int CRB_Tree::_Height(CRB_Node *pNode)
{
	if ( pNode == m_pNullNode )
	{
		return 0;
	}
	else
	{
		return max(_Height(pNode->left),_Height(pNode->right) ) +1;
	}
}

int CRB_Tree::GetHeight()
{
	return _Height(m_pRoot);
}

主函数测试

int _tmain(int argc, _TCHAR* argv[])
{
	CRB_Tree rbTree;
	
	
	rbTree.CreateRBT();

	rbTree.OutPut();
	
	
	cout<<endl<<"树的高度为："<<rbTree.GetHeight()<<endl;
	
	while (rbTree.m_pRoot != rbTree.m_pNullNode )
	{
		rbTree.Delete();
		rbTree.OutPut();
	}


	system("pause");
  	return 0;
}

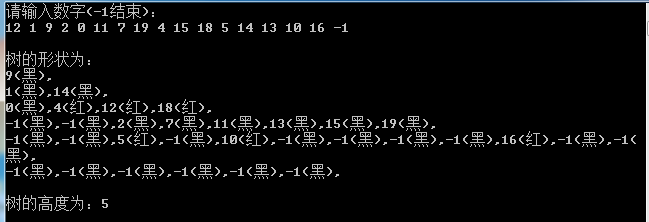
测试结果用图现实

以上是全部代码