算法学习笔记之二：从1到n的正数中1出现的次数

（记）

不能说好久没有学习算法了，应该是说好久没有码算法了。很多问题想着想着就理所当然以为就是如此，等真正码起来才会发现问题。所以对待实际算法问题要多“码”一点，能“码”则“码”

下面直入主题：

题目：输入一个整数n，求从1到n这n个整数的十进制表示中1出现的次数。

例如输入12，从1到12这些整数中包含1 的数字有1，10，11和12，1一共出现了5次。

题目可参见CSDN算法专家JULY的博文：

http://blog.csdn.net/v_JULY_v/article/details/6057286

另外作者也给出了解法参见：http://blog.csdn.net/v_JULY_v/article/details/6126444

今天偶然搜索发现了另一个比较新颖的算法：通过寻找规律，巧妙的利用了递归来求解。

我看到的原文出处是：http://blog.csdn.net/ysu108/article/details/7952455（具体的原作者就不考究了）

（一）思路分析

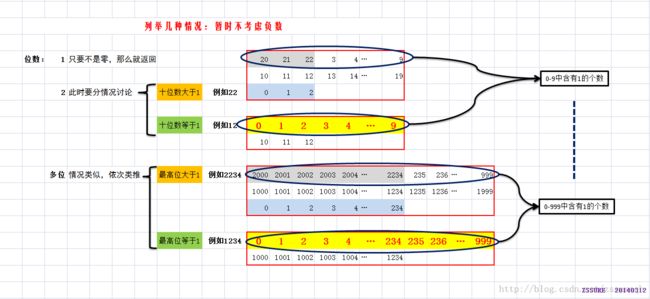
总结一下递归方法的思路：“就是将数字分成有规律的两部分”，如下图所示，通过将包含高位的部分数字移动到最前端，构成完成的0到9、0到99、0到999等等格式，来统计1出现的总个数，然后将去掉最高位后的数字进行递归求解，具体过程如下图所示（如下图中20、21、22、3、4、...、9以及2000、2001、...、2234、235、...、999）：

【图注:如图中椭圆所标记的区域所示，通过将包含最高位的部分数字移动来填补去除最高位后空缺的数字，从而凑成了完成的0-9、0-99、0-999等有规律的数列】

（二）自己码的结果

/*--------------------------------------------
	
	【30】.在从1到n的正数中1出现的次数（数组）
	题目：输入一个整数n，求从1到n这n个整数的十进制表示中1出现的次数。
	例如输入12，从1到12这些整数中包含1 的数字有1，10，11和12，1一共出现了5次。
	分析：这是一道广为流传的google面试题。
	

  --------------------------------------------*/
#include <stdio.h>
#include <cmath>
#include <string>
/*----------字符到数字的转换--------*/
//用字符串来模拟输入的数字可通过指针
//方便的控制位置的转换，便于递归函数实现
int Str2Num(char* str)
{
	if(NULL==str)
		return 0;
	int sum=0;
	while(*str)
	{
		sum=10*sum+(*str-'0');
		++str;
	}
	return sum;
}
/*--------求10的幂--------*/
int PowerOfTen(int n)
{
	int base=1;
	for(int i=0;i<n;++i)
		base*=10;
	return base;
}
/*----计算0-9、0-99、0-999等中数字1出现的个数-----*/
int NumOf9(int n)
{
	if(n==0)
		return 0;
	if(n==1)
		return 1;
	return 10*NumOf9(n-1)+PowerOfTen(n-1);
}
int CountAllOnes(char* strnum/*字符串形式的整数*/)
{
	if(NULL==strnum)
		return 0;
	int len=strlen(strnum);
	//如果是个位数，直接进行判别并返回
	if(len==1)
	{
		if(strnum[0]-'0')
			return 1;
		else
			return 0;
	}

	//不止个位数
	if(strnum[0]-'1')//如果最高位大于1
	{
		return PowerOfTen(len-1)+(strnum[0]-'0')*NumOf9(len-1)+CountAllOnes(strnum+1);
	}
	
	if(strnum[0]=='1')//如果最高位等于1
	{
		return Str2Num(strnum+1)+1+(strnum[0]-'0')*NumOf9(len-1)+CountAllOnes(strnum+1);
	}

};

int main()
{
	printf("请任意输入一个正整数：\n");
	char num[100];
	scanf("%s",num);
	if(num[0]=='-')
		printf("输入错误\n");
	printf("从1到%s中所有整数中1出现的次数为%d\n",num,CountAllOnes(num));
	return 0;
}

Author:zssure

E-mail:[email protected]

Date:2014-03-12