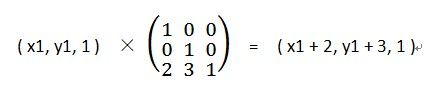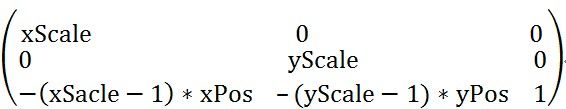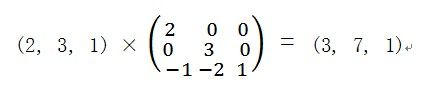Direct2D中的坐标变换
Direct2D中的坐标变换
例程源码下载
在3D世界中,坐标变换无处不在。在2D中,适当的运用坐标变换,可以对你的工作带来事半功倍的效果。我们借助Direct2D来看一下2D世界中的坐标变换。
一、 坐标变换简介
在3D中,坐标变换是通过一个4x4的矩阵来完成的。而在2D世界中,我们用到的矩阵是一个3x3矩阵。如下:
如果我们把这个矩阵当做一个2D矩形的话,其中xPos、yPos就是矩形左上角的坐标,Width、Height分别为矩形的宽和高。最后一列均为“哑元坐标”。
假设我们有一个点,其坐标为(x,y),我们用矩阵表示为: (x, y, 1)。同样1为哑元坐标。对坐标的变换就是对每一个点的变换。比如我们有一个矩形,我们想把它平移(或缩放、旋转、投射)到另一个地方,那么我们要做的只是将矩形的每个点变换到相应的位置就可以了。
比如此矩形上有一个点(x1, y1),我们想把此矩形在X、Y方向分别平移2和3个单位——亦即得到的坐标为(x1 + 2, y1 + 3)。我们就可以通过矩阵来完成了。我们将此坐标用矩阵表示,用如下变换:
可以看出得到的点就是我们要求的点。
二、 D2D坐标变换
知道怎么变换一个点,那么一个图形上的所有点都可以变换到新坐标。幸运的是,在D2D中,我们不必去手动为每一个点执行坐标变换,所有的变换操作都交由D2D完成。我们要做的只是给D2D一个变换矩阵和要操作的变换对象,其余的工作让D2D去做就是了。
现在唯一的关键是找出这样一个3x3的变换矩阵。这也不用担心了,因为D2D已经提供了这样一个类:Matrix3x2F。在实际工作中,我们看到3x3矩阵的最后一列是哑元坐标,所以不予考虑,只用3行2列来表示3x3矩阵。
Matrix3x2F提供了一系列静态方法来得到各种变换矩阵,你可以在http://msdn.microsoft.com/en-us/library/dd372275(v=VS.85).aspx找到此类的详细介绍。主要的一些列举如下:
static Matrix3x2F Matrix3x2F::Identity: 返回一个单位阵;
static Matrix3x2F Matrix3x2F::Translation: 执行平移变换;
static Matrix3x2F Matrix3x2F::Scale: 执行缩放;
static Matrix3x2F Matrix3x2F::Rotation: 执行旋转;
static Matrix3x2F Matrix3x2F::Skew: 执行投射变换。
可以看出,它们都返回一个Matrix3x2F类型的矩阵。
三、几种变换矩阵
我们可以通过上述静态方法得到一个变换矩阵,当然可以手动用代码写出一个变换矩阵。单位矩阵就是主对角线为1,其余全为0的矩阵。其余各种变换矩阵原理如下:
1> 平移矩阵(Translation):
我们已经看到了,平移矩阵只需将px设为X偏移,py设为Y偏移即可。
2> 缩放矩阵(Scale):
其中xScale、yScale分别是X、Y轴的缩放倍数,而xPos、yPos为缩放中心。比如我们有一个点(2, 3),我们要以(1, 1)为中心,分别在X、Y轴缩放2、3倍,那么得到的点如下:
那么我们最终得到的坐标就是(3, 7)。
3> 旋转矩阵(Rotation):
4> 投射矩阵(Skew):
投射的话我们直接用Skew函数就行了。需要注意的是:传递的参数中,X投射角度需要沿X轴逆时针的投射,Y投射角则要沿X轴顺时针投射。
另外我们需要注意的是:SetTransform函数调用后这种变换状态一直不变,直到下次调用SetTransform为止。如果我们想一次性执行多种变换,可以通过Matrix3x2F::SetProduct这个函数来将两次变换的矩阵相乘,来得到最终的变换矩阵。
需要注意的是,Matrix3x2F::SetProduct函数的参数传递次序影响着最终的变换矩阵。
四、Demo
1> 例程预览:
我们通过一个D2D例程来了解各种变换。如果你还没有准备D2D开发环境,请参看我的《Direct2D编程入门》一文,其中详细介绍了D2D入门所必须的知识。我们用C++来演示。先看程序最终截图,以便有个基本的认识:
在灰色背景基线上,我们分别绘制了变换前和变换后的各种图形。最后一个有斜射阴影的字符串绘制结合了投射、缩放、平移三种变换。如果你学会了这个例程,那么D2D的坐标变换大概就掌握了。
我分别用下面函数分次绘制了各个图形:
void DrawBaseLine(); //绘制参考基线. void DrawTranslationRectangle(); //绘制平移矩形. void DrawRotateRectangle(); //绘制一个旋转矩形. void DrawScaleRectangle(); //绘制一个缩放矩形. void DrawSkewText(); //绘制投影字体.
参考基线的绘制很简单,我们不再讲述。上述函数我们只讲述DrawRotateRectangle和DrawSkewText函数。其中DrawSkewText中包含了DrawTranslationRectangle和DrawScaleRectangle的全部知识。其余全部代码看附件,你可以用VS2008或VS2010编译。
2> DrawRotateRectangle函数:
void CD2DDemoApp::DrawRotateRectangle() { D2D1_RECT_F RenderRect = RectF(0.0f, 0.0f, 80.0f, 80.0f); //绘制透明度较大的没有旋转的矩形. m_pSolidBrush->SetColor(ColorF((ColorF::Blue), 0.3f)); m_pRenderTarget->SetTransform(Matrix3x2F::Translation(150.0f, 20.0f)); m_pRenderTarget->DrawRectangle( RenderRect, //要绘制矩形位置. m_pSolidBrush, //绘制所用画刷. 2.0f, //线宽. m_pStrokeStyle //线段风格. ); //先将矩形旋转,然后平移到所需位置. Matrix3x2F TransMatrix; TransMatrix.SetProduct( Matrix3x2F::Rotation(45.0f, Point2F(40.0f, 40.0f)), Matrix3x2F::Translation(150.0f, 20.0f) ); //绘制一个不透明的旋转后矩形. m_pSolidBrush->SetColor(ColorF(ColorF::Blue)); m_pRenderTarget->SetTransform(TransMatrix); m_pRenderTarget->DrawRectangle( RenderRect, m_pSolidBrush, 2.0f ); //绘制旋转提示. static const WCHAR wszText[] = _T("旋转变换示例"); m_pSolidBrush->SetColor(ColorF(ColorF::Red)); m_pRenderTarget->SetTransform(Matrix3x2F::Translation(150.0f, 130.0f)); m_pRenderTarget->DrawTextW( wszText, //提示字符串. wcslen(wszText), //绘制字符串的字符数. m_pDWriteTextFormat, //绘制所用字体格式. RectF(0.0f, 0.0f, 100.0f,10.0f), //绘制位置. m_pSolidBrush //绘制所用画刷. ); }
不难看出,所有的变换操作都是借助ID2D1HwndRenderTarget::SetTransform方法和Matrix3x2F结构来完成的。我们用Matrix3x2F::SetProduct将两个矩阵相乘来完成了旋转、平移的一次性操作。正如前面提到的:参数的传递次序决定着变换的结果。一般而言,我们变换的次序为:旋转(缩放、投射)à平移;即我们完成所有的变换后,再将图形平移到我们需要的地方。在旋转(或缩放、投射)过程中,我们一般以Point2F(0.0f, 0.0f) 来作为中心点(参考点)。
3> DrawSkewText函数:
void CD2DDemoApp::DrawSkewText() { static const WCHAR wszSkewText[] = _T("Hello, D2D!"); D2D1_RECT_F RenderSkewRect = RectF(0.0f, 0.0f, 600.0f, 300.0f); Matrix3x2F SkewScaleMatrix; //投射缩放矩阵. Matrix3x2F TransformMatrix; //最终的变换矩阵. // 先执行投射、缩放. SkewScaleMatrix.SetProduct( Matrix3x2F::Skew(-40.0f, 0.0f, Point2F(0.0f, 0.0f)), Matrix3x2F::Scale(1.0f, 0.6f, Point2F(0.0f, 0.0f)) ); // 再执行平移. TransformMatrix.SetProduct( SkewScaleMatrix, Matrix3x2F::Translation(80.0f, 205.0f) ); //绘制透明度较大的投射字符串. m_pSolidBrush->SetColor(ColorF(ColorF::Green, 0.3f)); m_pRenderTarget->SetTransform(TransformMatrix); m_pRenderTarget->DrawTextW( wszSkewText, //要绘制的宽字符类型字符串. wcslen(wszSkewText), //要绘制的字符个数.不能用-1替代!! m_pLargeTextFormat, //绘制所用字体格式. RenderSkewRect, //绘制位置. m_pSolidBrush //所用画刷. ); // // 再绘制不透明、不投射、不缩放的字符串. // m_pSolidBrush->SetColor(ColorF(ColorF::Blue)); m_pRenderTarget->SetTransform(Matrix3x2F::Translation(10.0f, 175.0f)); m_pRenderTarget->DrawTextW( wszSkewText, wcslen(wszSkewText), m_pLargeTextFormat, RenderSkewRect, m_pSolidBrush ); static const WCHAR wszText[] = _T("投射变换示例"); m_pSolidBrush->SetColor(ColorF(ColorF::Red)); m_pRenderTarget->SetTransform(Matrix3x2F::Translation(200.0f, 270.0f)); m_pRenderTarget->DrawTextW( wszText, wcslen(wszText), m_pDWriteTextFormat, RectF(0.0f, 0.0f, 100.0f, 30.0f), m_pSolidBrush ); }
特别注意的是,我们在绘制字符串时,给ID2D1HwndRenderTarget::DrawTextW函数中传递的字符串时WCHAR宽字符类型,第二个参数是要绘制的字符数。如果你想当然地像GDI+那样直接传递一个-1来表示所有字符的话,那就大错特错了,这样将绘制不出任何字符!!所以我们还是乖乖的传递要绘制的字符个数吧。
我们先执行了投射、缩放变换。我们用一个临时矩阵(SkewScaleMatrix)保存了这个变换结果,然后再在此基础上执行平移变换(通过Matrix3x2F::SetProduct实现)。最后统一用SetTransform执行全部变换。
最后我们绘制出没有执行任何变换的字符串,就出现了阴影效果。试着从各个方向拖动、拉动,没有任何闪烁,很酷,是吧!!
五、小结
通过一些简单的基础知识,介绍了坐标变换的基本内容。然后介绍了D2D中坐标变换的方式,以及Matrix3x2F结构的一些基础方法。最后通过一个C++实现的D2D例程详细实现了各种坐标变换。你可以下载例程源码详细体会D2D变换的各种细节操作。
【转载请注明出处】