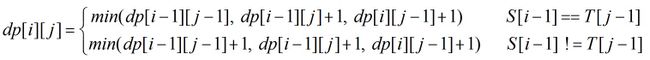浅谈文本的相似度问题

今天要研究的问题是如何计算两个文本的相似度。正如上篇文章描述，计算文本的相似度在工程中有着重要的应用，

比如文本去重，搜索引擎网页判重，论文的反抄袭，ACM竞赛中反作弊等等。

 

上篇文章介绍的SimHash算法是比较优秀的文档判重算法，它能处理海量文本的判重，Google搜索引擎也正是用这

个算法来处理网页的重复问题。实际上，仅拿文本的相似度计算来说，有很多算法都能解决这个问题，并且都达到比

较满意的效果。最常见的几种方法如下

 

   （1）基于最长公共子串

   （2）基于最长公共子序列

   （3）基于最少编辑距离

   （4）基于海明距离

   （5）基于余弦值

   （6）基于Jaccard相似度

 

由于前2种方法很经典，在实际中也用得不多，就不用多讲了。接下来主要介绍后面4种方法。

 

首先来研究基于最少编辑距离的方法。最少编辑距离是这样定义的：指两个字符串之间，由一个转化为另一个所需

要的最少编辑操作次数，允许的操作包括3种：将一个字符替换为另一个字符；插入一个字符；删除一个字符。

 

比如将kitten转换为sitting，则进行如下3步操作

 

    sitten  （k -> s）

    sittin  （e -> i）

    sitting （  + g ）

 

所以kitten与sitting的最少编辑距离就是3。编辑距离又称Levenshtein距离，也叫做Edit Distance，是俄

罗斯科学家Vladimir Levenshtein在1965年提出的。编程之美上的字符串相似度问题实际上就是求最少编辑距

离问题。

 

那么，如何求两个字符串的最少编辑距离？很明显这是一个DP问题，设表示字符串和字符串

的最少编辑距离，那么状态转移方程如下

 

       

 

初始化为

 

代码：

#include <iostream>
#include <string.h>
#include <stdio.h>
 
using namespace std;
const int N = 1005;
 
int dp[N][N];
char S[N],T[N];
 
int Lenv(char S[],char T[])
{
    int n = strlen(S);
    int m = strlen(T);
    for(int i=0; i<=n; i++)
        dp[i][0] = i;
    for(int i=0; i<=m; i++)
        dp[0][i] = i;
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=m; j++)
        {
            dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + 1;
            if(S[i-1] == T[j-1])
                dp[i][j] = min(dp[i][j],dp[i-1][j-1]);
            else
                dp[i][j] = min(dp[i][j],dp[i-1][j-1] + 1);
        }
    }
    return dp[n][m];
}
 
int main()
{
    while(scanf("%s%s",S,T)!=EOF)
        printf("%d\n",Lenv(S,T));
    return 0;
}

计算出两个文本的最少编辑距离之后，如果这个数字越小，那么说明这两篇文章越相似，但是很明显，通过这种方法

计算的时间复杂度为，而且需要两两进行计算，所以只适合处理小数据的文本。

 

对于基于海明距离的文本处理方法，有比较优秀的SimHash算法，上篇文章已经介绍过，不再赘述。

 

接下来研究基于余弦值的方法，其实基于余弦值的方法是依赖于向量空间模型的，它是先把文本进行分词，提取特征

向量，得到一个N维的文本向量，然后统计每个词在文中出现次数，把这个次数作为这个词的权值，某个词出现次数

越多，表示它越重要，得到的权值向量用表示。

 

如果要计算两个文本的相似度，那么应该先得到它们的权值向量和，进而相似度为

 

        

 

所以基于余弦值的相似度计算步骤大致如下

 

   

 

基于Jaccard相似度的度量也是先得到文本向量，这个向量可以看成是词的集合，那么两个集合之间的Jaccard相

似度等于交集大小与并集大小的比例。公式如下

 

       

 

当然在实际处理中计算交集与并集可以用红黑树等数据结构，在C++中直接可以考虑用set集合容器处理。