Ackerman函数以及 Linux环境下的绘图(perl脚本实现)
转自于 http://blog.chinaunix.net/uid-20602285-id-3078231.html
老师用ackerman函数来测试我们的lisp interpreter是否能应付extremely recursive function,虽然我们都不能,但也说明了一个健壮的interpreter是需要优化recursive function的一个道理。
ackerman函数 wiki 上有介绍:http://en.wikipedia.org/wiki/Ackerman_function
我下面记录的是怎么算出来A(4,2)。(如下表述中,ns就代表A)
ns(0,x) = x + 1
ns(1,x) = ns(0, ns(x-1)) && ns(1,0) = 2. so, ns(1,x) = x + 2
ns(2,x) = ns(1, ns(2,x-1)) = ns(2,x-1)+2 && ns(2,0) = ns(1,1) = 3. so, ns(2,x) = 2x+3
ns(3,x) = ns(2,ns(3,x-1)) = 2*ns(3,x-1)+3 && ns(3,0) = ns(2,1)=5. so, ns(3,x) = 2^(x+3) - 3
ns(4,x) = ns(3, ns(x-1)) = 2^(ns(3,x-1)+3) - 3 && ns(4,0) = ns(3,1) = 13
but if we let g(x) = ns(4,x) + 3
we have g(x) = 2^(g(x-1)) && g(0) = 16 = 24
so I think it's the end of this story (unless we use the symbol from knuth, which I just learned from wiki,
but I can manually get ns(4,2) = g(2) -3 = 2^(g(1)) - 3 = 2^(2^(g(0))) - 3 = 2^(216)) - 3 = 265536 - 3
these links may be helpful:
http://www.wolframalpha.com/input/?i=f%28x%29%3Df%28x-1%29%2B1%2Cf%280%29%3D2
http://www.wolframalpha.com/input/?i=f%28x%29+%3D+f%28x-1%29%2B2%2Cf%280%29%3D3
http://www.wolframalpha.com/input/?i=f%28x%29%3D2*f%28x-1%29%2B3%2Cf%280%29%3D5
http://www.wolframalpha.com/input/?i=f%28x%29%3D2^%28f%28x-1%29%2B3%29-3%2Cf%280%29%3D13
http://www.wolframalpha.com/input/?i=log2%28g%28x%29%29%3Dg%28x-1%29%2Cg%280%29%3D16
http://www.wolframalpha.com/input/?i=2^65536-3
当我算出来(4,2)后,我想尝试下得到ackerman函数的通式,结果后来尝试下后也可以了,需要引入wiki里学到的knuth发明的符号。“向上箭头符号”。↑
懂得这个符号以及扩展符号↑↑后,就可以证明ackerman函数的通式了,最傻瓜的方法是用归纳法证明,首先证明base case (1,1)成立,然后证明(1,x)成立;然后假设对于小于等于m的i或小于等于n的j (i,j)都成立,证明(i,j+1)成立。这样归纳法就完整了。
但是归纳法要求事先知道通式,这个不符合认识的流程。认识的流程应该是探索->猜想->证明。
以上我得出(4,2)的过程就是一个探索的过程。但是从中观察出规律确实很难,我也是在得到wiki的启发后知道的,接下来可以证明一下(4,x),有了knuth的符号,很容易证明;接下来再证明(5,x),也是可以的,无非knuth符号多了一层。最后再猜想,便很自然了。
ackerman函数通式的得出就写到这里。
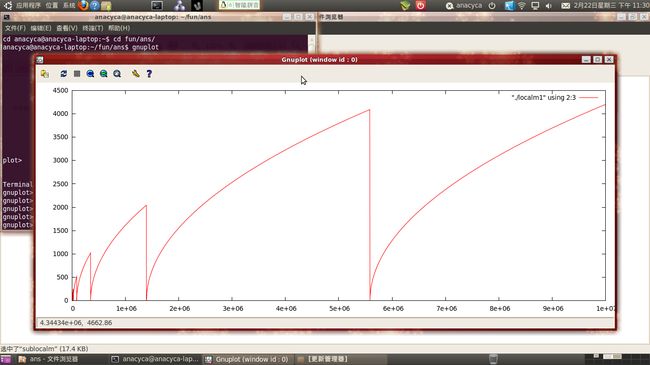
还有一个有趣的现象,是我一个同学冷潇泠想到的,他建议把函数递归过程中的B打印出来,并且配上递归层数i,形成一些(i,B)对,把这个画在坐标系上会形成无数个抛物线,且每个抛物线都是下个抛物线的前面部分。
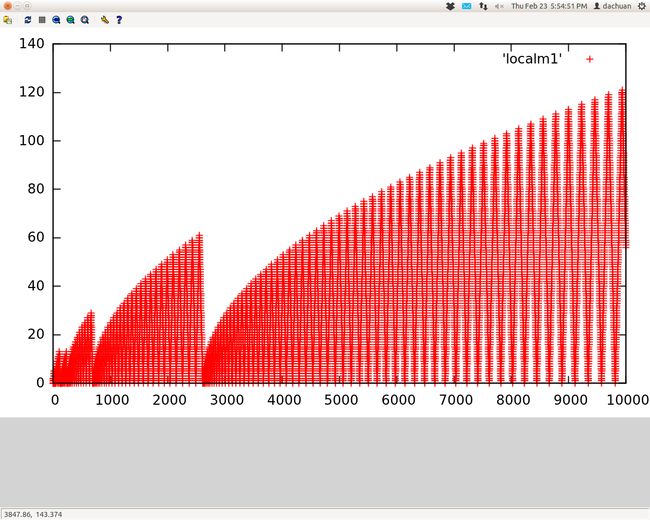
这个图也许还不清晰,把抛物线下的点都删掉,便有更清晰的图
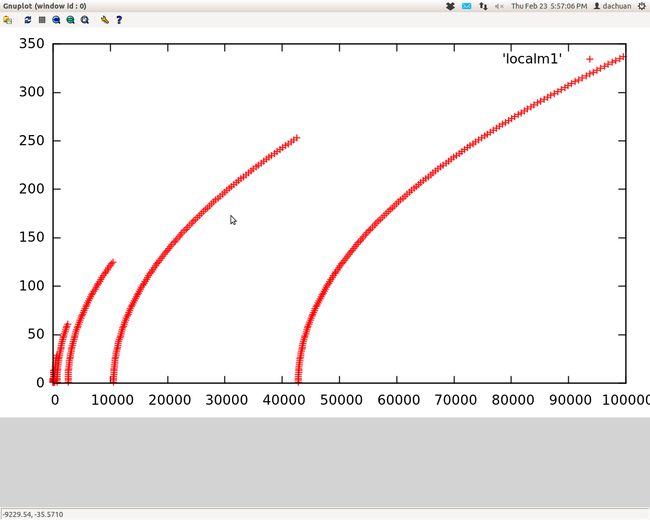
这个现象还是蛮有意思的。
我的ackerman函数实现如下:
- #include <stdio.h>
- #include <stdlib.h>
- int g = 0;
- int ackerman(int a, int b)
- {
- if(g++<100000) {
- printf("%d %d\n",a,b);
- }
- else
- exit(1);
- if(a==0)
- return b+1;
- else if (b==0)
- return ackerman(a-1,1);
- else
- {
- return ackerman(a-1,ackerman(a,b-1));
- }
-
- }
- int main()
- {
- int a,b;
- scanf("%d %d",&a,&b);
- ackerman(a,b);
- }
- #!/usr/bin/perl
- open(INP,"ackerman4.2.txt");
- open(OUT,">localm1");
- $a=0;
- $b=0;
- $c=0;
- $i=0;
- while(defined($line=<INP>))
- {
- @col=split(" ",$line);
- $a=$col[1]; #the 2nd column. B
- if(($a<$b)&&($b>$c))
- {
- #print OUT "$i ${col[0]} $b \n";
- print OUT "$i $b \n";
- #print OUT "$i $b \n";
- }
- $c=$b;
- $b=$a; #b = a. b is the temporary max
- $i++;
- }
- close(INP);
- close(OUT);
>plot 'localm1'
即可得出图片。
图片效果由于我不熟悉gnuplot便用得最原始的。
最后引用冷潇泠画的一个图,这个图更清晰。也是gnuplot。也可以用excel画。我都只知道理论上可画,但实际上都没经验。