2013 ACM-ICPC 亚洲区域赛 成都现场赛E (Exhausted Robot)
成都赛的几何题,现场没敢搞,今天有时间终于写过了
题意大概是给了一个矩形的房间,里面有n个凸多边形的家具,一个凸多边形的Robot,Robot可以任意平移,包括穿过家具,但是不能旋转,当Robot不和任何家具相交,且全部部分在房间内时,他的一个点(输入的第一个点)可以清理房间,然后问这个Robot可以清理的总面积是多少
做法是多边形绕多边形滑动 + 半平面交 + 多边形面积并
当我们正着没思路的时候,就可以反过来考虑,能清理的面积 = 房间总面积 - 不能清理的面积
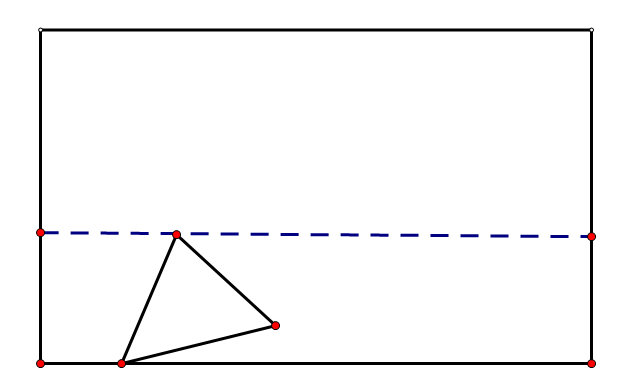
首先,受限于房间的边界,有一部分区域很容易可以判断不可清理,所以为了之后方便处理,我们优先把这些区域去掉,只需要求Robot的第一个点和上下左右四个方向最远点的竖直或水平距离,然后缩小房间边界即可,如下图
四个边都缩小以后,我们就得到了在不考虑家具的情况下,Robot可以清理的区域,同样还是为了方便处理,我把所有坐标平移,把房间的左下角变成(0, 0)
那么到这里,我们对于每一个家具独立考虑,如果能得到一个由该家具导致的不能清理区域,下一步我们只需要把若干个区域并起来就可以得到总的不可清理面积,于是问题的关键转变成了,一个多边形绕另一个多边形滑动一圈,第一个点形成的路径,这个路径其实就是不可清理区域的边界,可是这个区域直接求很麻烦,我们画图可以发现,如果我们让Robot的一个点在家具的边上滑动,或者Robot的一个边靠着家具的点滑动,我们都可以得到一条直线,并且在当前情况下,这个直线的左侧(看怎么画)就是不可达区域,那么我们枚举两个多边形的点和边,判断是否是一个合法的滑动,即如果这样滑动,多边形是否存在交,用叉乘判一下就可以了。这样我们得到若干半平面,求一次半平面交,就得到受某个家具影响所不能达到的区域,当然我们还要加4条边界半平面,就是那个矩形啦。最后把这些个半平面交得到的多边形求个面积并就解决了。
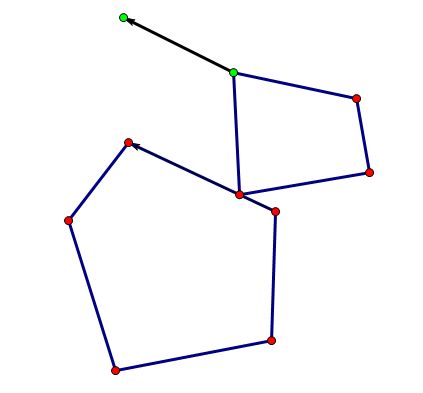
通过画图不难发现滑动的处理
中间那个多边形是我们当前枚举的家具,右上角的是Robot,那个绿点就是输入的第一个点,可以清理的,对于我们当前枚举的家具上的边,和Robot的点,只要这个边向量,叉乘Robot上的枚举点到其他点的向量都为负即可,同时这样滑动的状态下,上方的黑色直线就是所求,很显然他的方向是和我们枚举的边相同的,起点的话用这条边的点和Robot点之间的关系不难求出
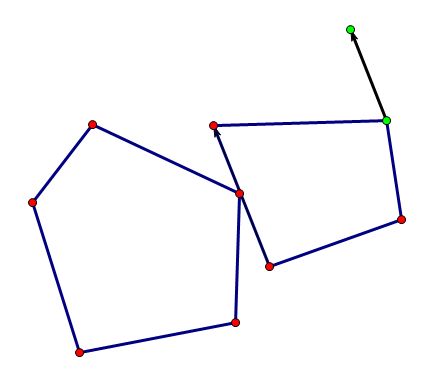
枚举Robot的边靠着家具的点滑动也是类似的,为了顺眼我顺时针枚举的边(不要在意这俩Robot为啥不一样,没画好而已...)
代码写了260行,不过关键的就60多行,其他的都是那些几何的东西,搞几何的都懂得>_<
另外我wa了一下午,特判了一下发现半平面交得到的多边形不严格凸,要求次凸包才可以过,不知道是不是精度误差的问题,如果有大牛知道望指点
下面是代码:
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <vector>
#include <map>
#include <string>
#include <set>
using namespace std;
#define eps 1e-8
#define LL long long
#define MP make_pair
#define mod 1000000007
#define mxn 25
int dcmp( double x ) {
return (x > eps) - (x < -eps);
}
struct point {
double x, y;
point(){}
point(double x, double y):x(x), y(y) {}
point operator + (const point &b) const {
return point(x + b.x, y + b.y);
}
point operator - (const point &b) const {
return point(x - b.x, y - b.y);
}
point operator * (const double &b) const {
return point(x * b, y * b);
}
bool operator < (const point &b) const {
return x < b.x || x == b.x && y < b.y;
}
void input() {
scanf( "%lf%lf", &x, &y );
}
}P[mxn * mxn], BL, TR, pnt[mxn * mxn], res[mxn * mxn];
struct line { //直线是点加方向向量表示
point p, v;
double ang;
line(){}
line( point p, point v ) :p(p), v(v) { ang = atan2(v.y, v.x); }
bool operator < ( const line &b ) const {
return ang < b.ang;
}
bool operator == (const line &b) const {
return dcmp(ang - b.ang) == 0;
}
}L[mxn * mxn], Q[mxn * mxn];
struct polygon {
point p[mxn * mxn];
int sz;
void input() {
scanf( "%d", &sz );
for( int i = 0; i < sz; ++i )
p[i].input();
p[sz] = p[0];
}
}R, F[mxn], g[mxn];
pair<double, int> C[mxn * mxn];
double dot( point a, point b ) {
return a.x * b.x + a.y * b.y;
}
double cross( point a, point b ) {
return a.x * b.y - a.y * b.x;
}
int andrew( int n ) {
sort( pnt, pnt + n );
int m = 0;
for( int i = 0; i < n; ++i ) {
while( m > 1 && dcmp(cross( res[m-1] - res[m-2], pnt[i] - res[m-1] )) <= 0 )
--m;
res[m++] = pnt[i];
}
int k = m;
for( int i = n - 2; i >= 0; --i ) {
while( m > k && dcmp(cross( res[m-1] - res[m-2], pnt[i] - res[m-1] )) <= 0 )
--m;
res[m++] = pnt[i];
}
if( n > 1 ) --m;
return m;
}
//半平面交
bool onleft( line l, point p ) {
return cross( l.v, p - l.p ) > 0;
}
point lineinter( line a, line b ) {
point u = a.p - b.p;
double t = cross( b.v, u ) / cross( a.v, b.v );
return a.p + a.v * t;
}
int halfplane( int n, int k ) {
sort( L, L + n);
int head = 0, tail = 0;
Q[tail] = L[0];
for( int i = 1; i < n; ++i ) {
while( head < tail && !onleft( L[i], P[tail-1] ) ) --tail;
while( head < tail && !onleft( L[i], P[head] ) ) ++head;
Q[++tail] = L[i];
if( dcmp( cross( Q[tail].v, Q[tail-1].v ) ) == 0 ) {
--tail;
if( onleft( Q[tail], L[i].p ) ) Q[tail] = L[i];
}
if( head < tail )
P[tail-1] = lineinter( Q[tail-1], Q[tail] );
}
while( head < tail && !onleft( Q[head], P[tail-1] ) ) --tail;
if( tail - head <= 1 ) return g[k].sz = 0;
P[tail] = lineinter( Q[tail], Q[head] );
int m = 0;
for( int i = head; i <= tail; ++i ) g[k].p[m++] = P[i];
g[k].p[m] = P[0];
return g[k].sz = m;
}
//多边形面积并
double segP( point a, point b, point c ) {
if( dcmp(b.x - c.x) )
return (a.x - b.x) / (c.x - b.x);
return (a.y - b.y) / (c.y - b.y);
}
double polyUnion( int n ) {
double sum = 0;
for( int i = 0; i < n; ++i )
for( int ii = 0; ii < g[i].sz; ++ii ) {
int tot = 0;
C[tot++] = MP(0, 0);
C[tot++] = MP(1, 0);
for( int j = 0; j < n; ++j ) if( i != j )
for( int jj = 0; jj < g[j].sz; ++jj ) {
int d1 = dcmp(cross(g[i].p[ii+1] - g[i].p[ii], g[j].p[jj] - g[i].p[ii]));
int d2 = dcmp(cross(g[i].p[ii+1] - g[i].p[ii], g[j].p[jj+1] - g[i].p[ii]));
if( !d1 && !d2 ) {
point t1 = g[j].p[jj+1] - g[j].p[jj];
point t2 = g[i].p[ii+1] - g[i].p[ii];
if( dcmp( dot(t1, t2) ) > 0 && j < i ) {
C[tot++] = MP(segP(g[j].p[jj], g[i].p[ii], g[i].p[ii+1]), 1);
C[tot++] = MP(segP(g[j].p[jj+1], g[i].p[ii], g[i].p[ii+1]), -1);
}
}
else if( d1 >= 0 && d2 < 0 || d1 < 0 && d2 >= 0 ) {
double d3 = cross(g[j].p[jj+1] - g[j].p[jj], g[i].p[ii] - g[j].p[jj]);
double d4 = cross(g[j].p[jj+1] - g[j].p[jj], g[i].p[ii+1] - g[j].p[jj]);
if( d2 < 0 )
C[tot++] = MP(d3 / (d3 - d4), 1);
else C[tot++] = MP(d3 / (d3 - d4), -1);
}
}
sort(C, C + tot);
double cur = min(max(C[0].first, 0.0), 1.0);
int sgn = C[0].second;
double s = 0;
for( int j = 1; j < tot; ++j ) {
double nxt = min(max(C[j].first, 0.0), 1.0);
if( !sgn ) s += nxt - cur;
sgn += C[j].second;
cur = nxt;
}
sum += cross(g[i].p[ii], g[i].p[ii+1]) * s;
}
return fabs(sum) / 2;
}
//根据Robot的形状缩小房间大小,并把房间左下角移动到(0, 0)
void Relax( int n ){
double dlt;
dlt = 0;
for( int i = 0; i < R.sz; ++i ) dlt = max(dlt, R.p[0].x - R.p[i].x);
BL.x += dlt;
dlt = 0;
for( int i = 0; i < R.sz; ++i ) dlt = max(dlt, R.p[i].x - R.p[0].x);
TR.x -= dlt;
dlt = 0;
for( int i = 0; i < R.sz; ++i ) dlt = max(dlt, R.p[0].y - R.p[i].y);
BL.y += dlt;
dlt = 0;
for( int i = 0; i < R.sz; ++i ) dlt = max(dlt, R.p[i].y - R.p[0].y);
TR.y -= dlt;
for( int i = 0; i < n; ++i )
for( int j = 0; j <= F[i].sz; ++j )
F[i].p[j] = F[i].p[j] - BL;
for( int i = 0; i <= R.sz; ++i )
R.p[i] = R.p[i] - BL;
TR = TR - BL;
BL = point(0, 0);
}
double solve( int n ) {
for( int i = 0; i < n; ++i ) {
polygon &t = F[i];
int m = 0;
L[m++] = line(point(0, 0), point(1, 0));
L[m++] = line(point(TR.x, 0), point(0, 1));
L[m++] = line(TR, point(-1, 0));
L[m++] = line(point(0, TR.y), point(0, -1));
//枚举家具的边和Robot的点
for( int j = 0; j < t.sz; ++j ) {
for( int k = 0; k < R.sz; ++k ) {
bool ok = true;
for( int l = 0; l < R.sz; ++l )
ok &= dcmp(cross(t.p[j+1] - t.p[j], R.p[l] - R.p[k])) <= 0;
if( ok )
L[m++] = line(point(t.p[j] + R.p[0] - R.p[k]), t.p[j+1] - t.p[j]);
}
}
//枚举Robot的边和家具的点
for( int k = 1; k <= R.sz; ++k ) {
for( int j = 0; j < t.sz; ++j ) {
bool ok = true;
for( int l = 0; l < t.sz; ++l )
ok &= dcmp(cross(R.p[k-1] - R.p[k], t.p[l] - t.p[j])) >= 0;
if( ok )
L[m++] = line(t.p[j] + R.p[0] - R.p[k], R.p[k-1] - R.p[k]);
}
}
halfplane(m, i);
//半平面交得到的多边形理论上是凸的,貌似是精度问题,凸的不严格
//不求一下凸包的话,多边形面积并的时候会有问题,卡了我一下午
for( int j = 0; j < g[i].sz; ++j ) pnt[j] = g[i].p[j];
g[i].sz = andrew(g[i].sz);
for( int j = 0; j < g[i].sz; ++j ) g[i].p[j] = res[j];
g[i].p[g[i].sz] = g[i].p[0];
}
return polyUnion(n);
}
int main()
{
int T, cas = 0, n;
scanf( "%d", &T );
while( T-- ) {
scanf( "%d", &n );
for( int i = 0; i < n; ++i )
F[i].input();
R.input();
BL.input(); TR.input();
Relax(n);
double ans = TR.x * TR.y - solve(n);
printf( "Case #%d: %.3lf\n", ++cas, ans );
}
return 0;
}