SimHash算法

首先，SimHash算法主要是用于文本去重的。文本去重的第一步就是判断文本的相似度，如果两个文本的相似度很

高，那么我们可以认为它们是相同的文本。

 

对于文本相似度的计算，传统的方法是使用向量空间模型（Vector Space Model），即VSM，VSM计算文本相似

度的方法是这样的：先对文本进行分词，提取出特征词，然后建立文本向量，把相似度的计算转化成某种特征向量

距离的计算，比如余弦夹角，欧氏距离计算等等。这样做结果就是，如果文本向量的维度很高，那么计算的代价会

很大，所以必须另辟蹊径。

 

可以看出，VSM计算文本的相似度是两两文本进行计算比较，对于小数量文本处理是可以的。但对于百度，Google这

样的搜索引擎，爬虫每天爬取的网页数目大得惊人，对于新爬取的网页，为了防止重复收录网页，需要对网页进行判

重处理，对于这样的海量数据，VSM无能为力。所以针对这种海量文本的去重，Google提出了SimHash算法，它把高

维度的文本向量映射成一个指纹，进行降维，从而减少计算量。

 

SimHash算法的步骤如下

 

  （1）输入一个N维的文本特征向量V，每个特征具有一定权重

  （2）初始化一个C维的向量Q为0，C位的二进制签名S为0

  （3）对于向量V的每一个特征，使用传统Hash算法计算出一个C位的散列值H。对1<=i<=C，如果H的第i位

      为1， 则Q的第i个元素加上该特征的权重；否则，Q的第i个元素减去该特征的权重。

  （4）如果Q的第i个元素大于0，则S的第i位为1，否则为0

  （5）返回这个C位的二进制签名S

 

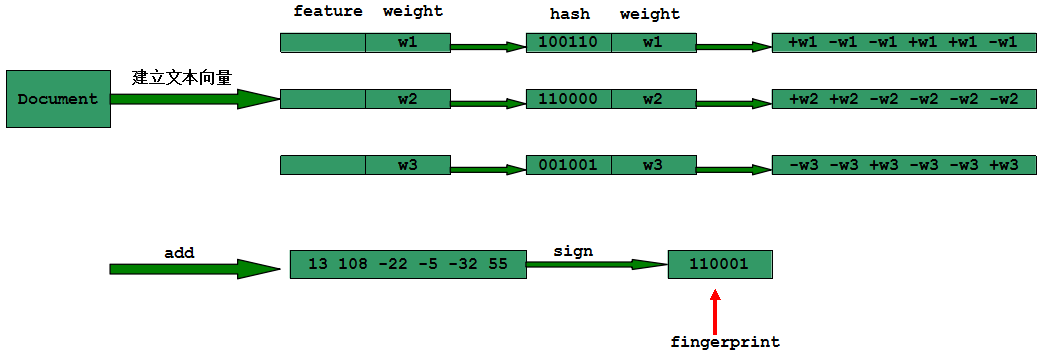
下面以N = 3为例进行如图说明

 

 

对每篇文档根据SimHash算出签名S后，再计算两个签名的海明距离，海明距离等于这两个二进制数异或后1的个数。根据经验，对于64位的SimHash，海明距离在3以内的都可以认为相似度比较高。

 

可以看出经过SimHash算法得到的是一个文档的指纹，我们根据这个指纹来判断文档的相似度，前面说过，如果海明

距离在3以内，那么就认为这两个文档基本是相同的。以64位的指纹来说，把它以每16位划分块，如果两个指纹海明

距离小于等于3，那说明至少有一个16位块完全相同（组合数学里的鸽巢原理）。但是我们不知道具体是哪两个块相

同，所以要进行枚举，这里只需要枚举4次。

 

以8位的数字指纹01100011来说明

我们划分为4块，每块两位，即01 10 00 11，然后在所有的8位二进制签名中分别查找以01，10，00，11开始的签

名。当然在这所有的8位二进制签名数据中，我们可以以前两位进行索引，比如把01000000和01111111放在一个簇

中，如果找不到以01，10，00，11开始的二进制签名，说明海明距离肯定大于3，这样就直接可以判断这两个文本不

相似，否则再比较后面的部分。

 

以上是8位二进制签名的比较方法，64位的签名类似方法处理。

 

假如现在有10亿个签名，约为2^34，那么每个块最多可能有2^(34-16)=262144个结果，那么4个块最终比较次数为

4*262144，大约为100万，这样原本需要比较10亿次，现在只需要比较100万次，可以看出计算量大大减少。

 

问题：有10亿个不重复的64位01串，再另给一个64位的01串str，如何快速从这10亿个串中找出与str的海明距离小

     于等于3的字符串？

 

代码：

#coding:utf-8
 
class SimHash:
 
    def __init__(self, tokens='', hashbits=128):
        self.hashbits = hashbits
        self.hash = self.simhash(tokens)
 
    def __str__(self):
        return str(self.hash)
 
    def simhash(self, tokens):
        v = [0] * self.hashbits  #等价于定义一个长度为hashbits的列表，列表中的元素全为0
        for t in [self.string_hash(x) for x in tokens]:
            for i in range(self.hashbits):
                bitmask = 1 << i
                if t & bitmask:
                    v[i] += 1
                else:
                    v[i] -= 1
        fingerprint = 0
        for i in range(self.hashbits):
            if v[i] >= 0:
                fingerprint += 1 << i
        return fingerprint
 
    def hamming_distance(self,other):
        x = (self.hash^other.hash ) & ((1 << self.hashbits) - 1)
        cnt = 0
        while x:
            cnt += 1
            x &= x - 1
        return cnt
 
    def similarity(self,other):
        a = float(self.hash)
        b = float(other.hash)
        if a > b:
            return b / a
        else:
            return a / b
 
    def string_hash(self,source):
        if source == '':
            return 0
        else:
            x = ord(source[0]) << 7
            m = 1000003
            mask = 2 ** self.hashbits - 1
            for c in source:
                x = ((x * m) ^ ord(c)) & mask
            x ^= len(source)
            if x == -1:
                x = -2
            return x
 
if __name__ == '__main__':
    s = 'This is a test string for testing'
    hash1 = SimHash(s.split())
 
    s = 'This is a test string for testing also'
    hash2 = SimHash(s.split())
 
    s = 'Hello ,World!!!'
    hash3 = SimHash(s.split())
 
    print hash1.hamming_distance(hash2),'  ',hash1.similarity(hash2)
    print hash1.hamming_distance(hash3),'  ',hash1.similarity(hash3)