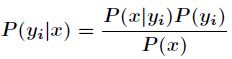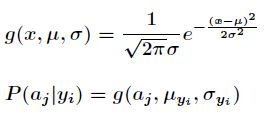朴素贝叶斯分类

今天，我学习了朴素贝叶斯分类，接下来，我会详细讲述它的原理以及在文本分类中的应用。

 

Contents

 

  1. 分类问题的定义

  2. 贝叶斯定理

  3. 贝叶斯分类原理

  4. 特征属性划分的条件概率及Laplace校准

  5. 贝叶斯文本分类实例

 

 

1. 分类问题的定义

 

   已知集合和集合，确定映射规则，使得任意，有

   且仅有一个使得成立。其中叫做类别集合，每一个元素是一个类别；叫做项集合，每一

   个元素是一个待分类的项；叫做分类器。分类算法的任务就是构造分类器。

 

 

2. 贝叶斯定理

  

   朴素贝叶斯分类是基于贝叶斯定理的，定理表述如下

     

       

 

   此公式证明如下，因为

 

       

 

   联立两式消去，得到

 

       

 

   贝叶斯定理为我们打通了从获得的道路。

 

 

3. 贝叶斯分类原理

 

   朴素贝叶斯分类的原理是这样的：对于给定的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大

   就认为此待分类项属于哪个类别。

 

   朴素贝叶斯分类的正式定义如下

 

   （1）设为一个待分类项，其中为的一个特征属性，一共有个特征属性。

   （2）类别集合为

   （3）分别计算

   （4）如果，则。

 

   可以看出最关键的问题是如何求出（3）中的各个条件概率。关于这个关键问题，可以这样做

 

   （1）找到一个已知分类的待分类项集合，这个集合叫做训练样本集。

   （2）统计各个类别下各个特征属性的条件概率估计。即得到

 

      

 

   （3）如果各个特征属性是条件独立的，则根据贝叶斯定理有如下推导

 

       

 

       分母对所有类别来说为常数，只需考虑分子的最大值即可，又因为各特征属性是条件独立的，所以

 

       

      

   所以综上，朴素贝叶斯分类的流程大致可以用下图来描述

 

   

 

 

4. 特征属性划分的条件概率及Laplace校准

 

   现在来讨论如何计算

 

   当特征属性为离散值时，只要统计出训练样本中各个属性在每个类别中出现的频率即可用来估计。

   当特征属性为连续性时，情况又是怎样的呢？当特这属性为连续性时，假设其值服从高斯分布，即

 

    

 

   那么，只要计算出训练样本中类别中特征的均值和标准差，那么带入上式便可得到条件概率的估计值。

 

   比如特征属性为身高或者体重等等，就不是简单地统计出现次数来估计概率了。需要计算均值和标准差来估计。

 

   接下来，考虑当怎么办？ 这种情况的出现是因为某个类别下某个特征属性没有出现，这种情况的

   出现会导致分类器的质量大大降低。为了解决这个问题，就引入了Laplace校准，核心思想就是如果某个类别

   下某个特征属性没有出现，那么就让它的计数器加1，即让它出现一次。这样就避免了的局面。

 

 

5. 贝叶斯文本分类实例

 

   利用朴素贝叶斯分类的实例有很多，比如文本分类，检测SNS社区中不真实的账号，根据人体特征预测性别等等。

   在进行文本分类之前，需要对文本的特征属性进行选择，这一步很关键，关于文本的特征属性选择参考之前的文

   章《文本特征属性选择》。

 

   在朴素贝叶斯文本分类问题中，与两个重要的模型，即多项式模型和伯努利模型。其实这两种模型并不高深，只

   是在计算先验概率和条件概率时有差别，多项式模型会统计词频，而伯努利模型针对出现过的词仅标记为1，没有

   出现过就标记为0，可以看出一个是基于词频，一个是基于文档频率。在计算条件概率时，当待分类文本中的某个

   词没有出现在词库中时，概率为零，会导致严重的问题，需要考虑拉普拉斯平滑，将所有词出现的次数都加1。再

   进行统计。如果概率太小而词数太多，可能会超double，那么可以取对数将乘法改为加法计算。

 

   当然在朴素贝叶斯分类中，如果特征属性是连续的值，比如身高，那么就用高斯分布来处理。从整体来说，朴素

   贝叶斯算法是比较好简单的，所以就不用C++实现了。