POJ 1609 Tilining Up Blocks

 

Tiling Up Blocks

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 3016		Accepted: 1148

Description

Michael The Kid receives an interesting game set from his grandparent as his birthday gift. Inside the game set box, there are n tiling blocks and each block has a form as follows: 

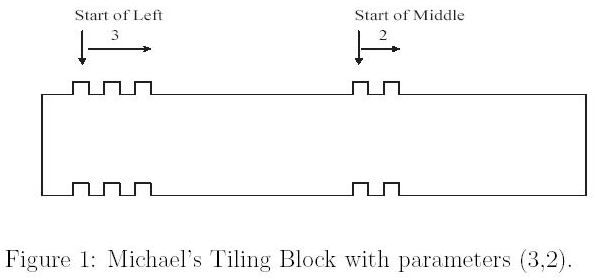
Each tiling block is associated with two parameters (l,m), meaning that the upper face of the block is packed with l protruding knobs on the left and m protruding knobs on the middle. Correspondingly, the bottom face of an (l,m)-block is carved with l caving dens on the left and m dens on the middle. 
It is easily seen that an (l,m)-block can be tiled upon another (l,m)-block. However,this is not the only way for us to tile up the blocks. Actually, an (l,m)-block can be tiled upon another (l',m')-block if and only if l >= l' and m >= m'. 
Now the puzzle that Michael wants to solve is to decide what is the tallest tiling blocks he can make out of the given n blocks within his game box. In other words, you are given a collection of n blocks B = {b1, b2, . . . , bn} and each block bi is associated with two parameters (li,mi). The objective of the problem is to decide the number of tallest tiling blocks made from B. 

Input

Several sets of tiling blocks. The inputs are just a list of integers.For each set of tiling blocks, the first integer n represents the number of blocks within the game box. Following n, there will be n lines specifying parameters of blocks in B; each line contains exactly two integers, representing left and middle parameters of the i-th block, namely, li and mi. In other words, a game box is just a collection of n blocks B = {b1, b2, . . . , bn} and each block bi is associated with two parameters (li,mi). 
Note that n can be as large as 10000 and li and mi are in the range from 1 to 100. 
An integer n = 0 (zero) signifies the end of input.

Output

For each set of tiling blocks B, output the number of the tallest tiling blocks can be made out of B. Output a single star '*' to signify the end of 
outputs.

Sample Input

3
3 2
1 1
2 3
5
4 2
2 4
3 3
1 1
5 5
0

Sample Output

2
3
*

Source

Asia Kaohsiung 2003

 

 

/* 这题主要是求最大升序子序列，但是由于数据规模是n = 10000，所以 如果用常规dp时间复杂度为n ^ 2很容易从超时，所以就想到了二分法DP，时间 复杂度是nlgn 二分法DP查询主要需要维护两个数组: 一个是 longgest[i] 记录以第i个元素结尾可以构成的最长上升子序列 另一个是smallest[l][2] 记录长度为l的最长上升子序列结尾值的最小可能值 先对输入数据排序，然后一次处理每一个元素，当处理到元素i的时候，需要 用二分法去查询i可以插入的合适位置，假设i的查询最终落在k位置上 1)如果k < i，则需要判断i是否可以更新smallest[l] 因为这时input[i]和input[k]有两种大小关系，input[i]不一定比input[k]更小, 由于整个序列 已经按照l进行排序了，所以l不用比较，我们所要做的就是使right值更小，较input[i].r和smallest[k][1]， 如果前者小于后者则更新 另外需要更新longest[i] = k; 2)如果k == i，则表示数据i是当前最大的数据 所以置longest[i] = i, smallest[i] = input[i]即可 */ #include <iostream> #include <algorithm> #define MAX_N 10000 using namespace std; struct input { int l, r; }inputs[MAX_N + 1]; bool compare(const input &i1, const input &i2) { if(i1.l < i2.l) return true; else if(i1.l == i2.l) { if(i1.r <= i2.r) return true; else return false; } else return false; } int longgest[MAX_N + 1]; //lonngest[i] 记录以第i个元素结尾可以构成的最长上升子序列 int smallest[MAX_N + 1][2]; //smallest[l] 记录长度为l的最长上升子序列结尾值的最小可能值 int n; int main() { int i, maxLen; while(scanf("%d", &n) && n != 0) { maxLen = INT_MIN; for(i = 1; i <= n; i++) scanf("%d%d", &inputs[i].l, &inputs[i].r); sort(&inputs[1], &inputs[1] + n, compare); int curLen = 0, left, right, lval, rval, mid; for(i = 1; i <= n; i++) { lval = inputs[i].l; rval = inputs[i].r; left = 1; right = curLen; while(left <= right) { mid = (left + right) / 2; if(smallest[mid][1] <= rval) left++; else right--; } longgest[i] = left; if(curLen == 0 || (lval <= smallest[left][0] && rval < smallest[left][1])) smallest[left][0] = lval; smallest[left][1] = rval; if(left > curLen) curLen = left; if(longgest[i] > maxLen) maxLen = longgest[i]; } printf("%d/n", maxLen); } printf("*/n"); return 0; }