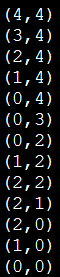迷宫问题(栈，递归，队列)

这个迷宫问题的解答，主要参考了《LINUX一站式编程》中的第12章“栈与队列”的正文和习题。

 假设有这样一个迷宫，用一个5*5的数组来表示，其中0表示有路可走，1表示无路可走。那么，如何找到一个通路，使得可以从左上角的(0,0)点走到右下角的(4,4)点？

迷宫

0	1	0	0	0
0	1	0	1	0
0	0	0	0	0
0	1	1	1	0
0	0	0	1	0

分成三个办法来解决这个问题。堆栈，递归和队列。

第一种，使用堆栈进行深度优先搜索。堆栈的先进后出实现了深度优先搜索。其中，如果一个点被探测过了，就标记为2，避免以后重复探索。为了记载历史路径信息，使用了predecessor数组。代码和解如下：

//堆栈版迷宫问题
struct point{int row, col;} stack[512];
int top = 0;
int LEN=5;
int maze[5][5] = {
    0,1,0,0,0,
    0,1,0,1,0,
    0,0,0,0,0,
    0,1,1,1,0,
    0,0,0,1,0,
 };
void push(struct point p)
{
    stack[top++] = p;
    return;
}
struct point pop()
{
    return stack[--top];
}
int is_empty()
{
    return top == 0;
}
void print_maze()
{
    int i,j;
    for(i=0;i<LEN;i++)
    {
        for(j=0;j<LEN;j++)
            printf("%d",maze[i][j]);
        putchar('\n');
    }
    printf("**********\n");
}
struct point predecessor[5][5] = {
    {{-1,-1},{-1,-1},{-1,-1},{-1,-1},{-1,-1}},
    {{-1,-1},{-1,-1},{-1,-1},{-1,-1},{-1,-1}},
    {{-1,-1},{-1,-1},{-1,-1},{-1,-1},{-1,-1}},
    {{-1,-1},{-1,-1},{-1,-1},{-1,-1},{-1,-1}},
    {{-1,-1},{-1,-1},{-1,-1},{-1,-1},{-1,-1}},
};
void visit (int row, int col, struct point pre)
{
    struct point visit_point = {row, col};
    maze[row][col] = 2;
    predecessor[row][col] = pre;
    push(visit_point);
}
int main()
{
    struct point p = {0,0};
    int MAX_ROW = 5;
    int MAX_COL = 5;
    maze[p.row][p.col] = 2;
    push(p);
    while(!is_empty()) {
        p = pop();
        if(p.row ==  MAX_ROW -1 && p.col == MAX_COL -1)
            break;
        if(p.col+1< MAX_COL && maze[p.row][p.col+1] == 0)
            visit(p.row,p.col+1,p);
        if(p.row+1< MAX_ROW && maze[p.row+1][p.col] == 0)
            visit(p.row+1,p.col,p);
        if(p.col-1>=0 && maze[p.row][p.col-1] == 0)
            visit(p.row,p.col-1,p);
        if(p.row-1>=0 && maze[p.row-1][p.col] == 0)
            visit(p.row-1,p.col,p);
        print_maze();
    }
    if(p.row == MAX_ROW -1 && p.col == MAX_COL -1) {
        printf("(%d,%d)\n",p.row,p.col);
        while(predecessor[p.row][p.col].row != -1) {
            p = predecessor[p.row][p.col];
            printf("(%d,%d)\n",p.row,p.col);
        }
    } else {
        printf("No Path\n");
    }
    return 0;
}

运行结果如下

第二种，使用递归(系统帮你进行了深度优先搜索)

系统在递归调用时，系统内部有一个堆栈，所以使用递归时，虽然你没有显示地使用堆栈，但是系统内部的堆栈也能起到和第一种方法相同的功能。代码和的解答如下：

//递归版迷宫问题
struct point{int row, col;} stack[512];
int top = 0;
int MAX_ROW=5, MAX_COL=5;
int maze[5][5] = {
    0,1,0,0,0,
    0,1,0,1,0,
    0,0,0,0,0,
    0,1,1,1,0,
    0,0,0,1,0,
 };
void push(struct point p)
{
    stack[top++] = p;
    return;
}
struct point pop()
{
    return stack[--top];
}
int is_empty()
{
    return top == 0;
}
void print_maze()
{
    int i,j;
    for(i=0;i<MAX_ROW;i++)
    {
        for(j=0;j<MAX_COL;j++)
            printf("%d",maze[i][j]);
        putchar('\n');
    }
}
struct point predecessor[5][5] = {
    {{-1,-1},{-1,-1},{-1,-1},{-1,-1},{-1,-1}},
    {{-1,-1},{-1,-1},{-1,-1},{-1,-1},{-1,-1}},
    {{-1,-1},{-1,-1},{-1,-1},{-1,-1},{-1,-1}},
    {{-1,-1},{-1,-1},{-1,-1},{-1,-1},{-1,-1}},
    {{-1,-1},{-1,-1},{-1,-1},{-1,-1},{-1,-1}},
};
void visit (int row, int col, struct point pre)
{
    maze[row][col] = 2;
    predecessor[row][col] = pre;
}
void tranverse_maze(struct point& p)
{
    std::cout<<"---------"<<std::endl;
    print_maze();
    std::cout<<"---------"<<std::endl;
    std::cout<<p.row<<","<<p.col<<std::endl;
    if(p.row == MAX_ROW -1 && p.col == MAX_COL -1)
    {
        return;
    } else if (p.row+1<=MAX_ROW -1 && maze[p.row+1][p.col] == 0) {
        visit(p.row+1,p.col,p);
        p.row++;
        tranverse_maze(p);
    } else if (p.col-1>=0 && maze[p.row][p.col-1] == 0) {
        visit(p.row,p.col-1,p);
        p.col--;
        tranverse_maze(p);
    } else if (p.row-1>=0 && maze[p.row-1][p.col] == 0) {
        visit(p.row-1,p.col,p);
        p.row--;
        tranverse_maze(p);
    } else if (p.col+1<=MAX_COL-1 && maze[p.row][p.col+1] == 0) {
        visit(p.row,p.col+1,p);
        p.col++;
        tranverse_maze(p);
    } else {
        p.row=predecessor[p.row][p.col].row;
        p.col=predecessor[p.row][p.col].col;
        tranverse_maze(p);
        return;
    }
}
int main()
{
    print_maze();
    struct point p = {0,0};
    int MAX_ROW = 5;
    int MAX_COL = 5;
    maze[p.row][p.col] = 2;
    tranverse_maze(p);
   if(p.row == MAX_ROW -1 && p.col == MAX_COL -1) {
        printf("(%d,%d)\n",p.row,p.col);
        while(predecessor[p.row][p.col].row != -1) {
            p = predecessor[p.row][p.col];
            printf("(%d,%d)\n",p.row,p.col);
        }
    } else {
        printf("No Path\n");
        std::cout<<"---------"<<std::endl;
        std::cout<<p.row<<","<<p.col<<std::endl;
    }
    return 0;
}

运行结果如下

第三种，使用队列进行广度优先搜索

队列的先进先出实现了广度优先搜索。并且，在这个问题中，广度优先搜索和前两种方法相比的优势在于：

一，如果迷宫问题的解不止一个，那么广度优先搜索一定能够找到最短路径的解。因为，广度优先搜索的先进先出的特点，说明，它必定是先考虑了和目标点距离为1的所有候选点能否构成到达目标点的通路之后，再考虑和目标点距离为2的所有候选点能否构成到达目标点的通路，再考虑和目标点距离为3的所有点能否构成到达目标点的通路，以此类推，直到走到目标点位置。

二，广度优先搜索使用了队列，队列的head和tail指向的空间被放置了数据之后，就不会继续放数据了，所以这个空间的使用次数只有一次。这个和第一种方法中的栈不同，栈的top不停地push和pop，所以top所在的空间的使用次数可以为多次。队列的空间使用效率低于栈，这个trade-off的好处是，栈中用来记录探索通路的历史路径信息的predecessor数组的空间可以省下来。具体代码如下：

//队列版迷宫问题
struct point{int row, col,predecessor;} queue[512];
int head = 0, tail = 0;
int MAX_ROW=5,MAX_COL=5;

int maze[5][5] = {
    0,1,0,0,0,
    0,1,0,1,0,
    0,0,0,0,0,
    0,1,1,1,0,
    0,0,0,1,0,
 };

void enqueue(struct point p)
{
    queue[tail++] = p;
    return;
}

struct point dequeque()
{
    return queue[head++];
}

int is_empty()
{
    return head == tail;
}

void print_maze()
{
    int i,j;
    for(i=0;i<MAX_ROW;i++)
    {
        for(j=0;j<MAX_COL;j++)
            printf("%d",maze[i][j]);
        putchar('\n');
    }
    printf("**********\n");
}

void visit (int row, int col)
{
    struct point visit_point = {row, col,head-1};
    maze[row][col] = 2;
    enqueue(visit_point);
}

int main()
{
    struct point p = {0,0,-1};
    int MAX_ROW = 5;
    int MAX_COL = 5;
    maze[p.row][p.col] = 2;
    enqueue(p);
    while(!is_empty()) {
        p = dequeque();
        if(p.row ==  MAX_ROW -1 && p.col == MAX_COL -1)
            break;
        if(p.col+1< MAX_COL && maze[p.row][p.col+1] == 0)
            visit(p.row,p.col+1);
        if(p.row+1< MAX_ROW && maze[p.row+1][p.col] == 0)
            visit(p.row+1,p.col);
        if(p.col-1>=0 && maze[p.row][p.col-1] == 0)
            visit(p.row,p.col-1);
        if(p.row-1>=0 && maze[p.row-1][p.col] == 0)
            visit(p.row-1,p.col);
//        print_maze();
    }
    if(p.row == MAX_ROW -1 && p.col == MAX_COL -1) {
        printf("(%d,%d)\n",p.row,p.col);
        while(p.predecessor!= -1) {
            p = queue[p.predecessor];
            printf("(%d,%d)\n",p.row,p.col);
        }
    } else {
        printf("No Path\n");
    }
    return 0;
}

运行结果如下