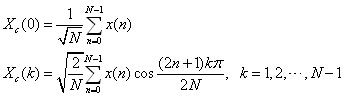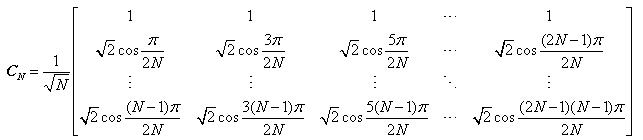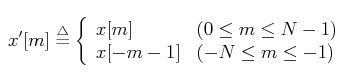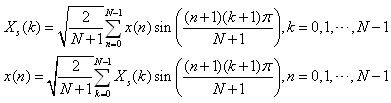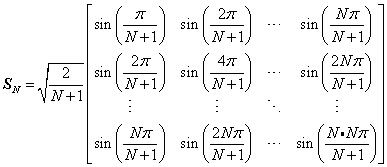压缩感知稀疏基之离散余弦变换(DCT)和离散正弦变换(DST)

题目：压缩感知稀疏基之离散余弦变换(DCT)和离散正弦变换(DST)

在前面一篇《压缩感知的常见稀疏基名称及离散傅里叶变换基》中集结了九篇压缩感知文献中有关稀疏基名称，并且直白地告诉大家稀疏基其实就是某种正交变换的变换矩阵列向量组成的基，最后还说了离散傅里叶变换基。对于离散傅里叶变换基前面乘了一项N的开方，这其实就是一个定标因子，为得是将变换矩阵归一化，使各个列向量组成的基为标准(规范)正交基。在这一篇里将简单介绍离散余弦变换和离散正弦变换并说明它们的基在Matlab里的生成方法。以后也就不再提“XX基”了，直接说“XX变换”吧。

一、离散余弦变换(Discrete Cosine Transform,DCT)

按现在的正交变换理论 ，DCT共有八种，分别称为DCT-Ⅰ、DCT-Ⅱ、DCT-Ⅲ、DCT-Ⅳ、DCT-Ⅴ、DCT-Ⅵ、DCT-Ⅶ、DCT-Ⅷ，其中常用的是前四种，而前四种中更常用的是DCT-Ⅰ和DCT-Ⅱ，它们二者间更常用的是DCT-Ⅱ，一般我们提到DCT而不特殊说明即指DCT-Ⅱ，图像压缩中用的也是DCT-Ⅱ。

八种DCT是分别提出来的，经后人归纳总结分别称为DCT-Ⅰ~ DCT-Ⅷ，其中最早于1974年在文献【1】中提出DCT（即DCT-Ⅱ）:

要想使上面的DCT的变换矩阵列向量成为单位向量，定标因子得变换一下，这里还是以文献【2】中的定义式为准，因为它的变换矩阵直接是正交矩阵（正交阵是自身与自身的转置相乘等于单位阵，即矩阵的转置与矩阵的逆相等）：

因此可得到变换矩阵C_N

可以验证，变换矩阵C_N是一个正交矩阵。

二、离散余弦变换与离散傅里叶变换的关系

在文献【3】中提到“离散余弦变换相当于一个长度大概是它两倍的离散傅里叶变换，这个离散傅里叶变换是对一个实偶函数进行的（因为一个实偶函数的傅里叶变换仍然是一个实偶函数），在有些变形里面需要将输入或者输出的位置移动半个单位”，为了理解这段话，实际上是为了挖掘DCT与DFT的关系，我思考了好久（当然也没思考明白）：实序列的DFT是共轭对称的，实偶序列的DFT是实对称的，也就是说对一个实偶序列进行DFT分析的话无论是时域还是频域都是实数，避免了复数计算（DCT的优点），然而由于实偶序列的DFT是实对称的，因此数据有一半的冗余，应该只要一半的结果就可以了，那么怎么变一下就可以得到这么一种变换呢？这会不会就是DCT呢？思考了好久也没想明白，最后看到了新浪一篇博客【4】，进而看到了一个英文网页【5】：

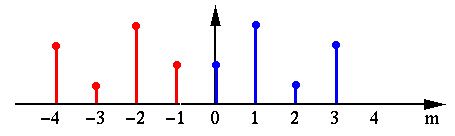
将一个序列向负半轴方向翻折拓展一个周期：

即将蓝色部分以m=-0.5为对称轴翻转得到红色部分。这个时候得到的新序列并不是偶对称的，它以m=-0.5为对称轴，将序列向右移动0.5即可得到一个偶对称序列：

对移位后的得到的偶对称序列进行DFT变换：

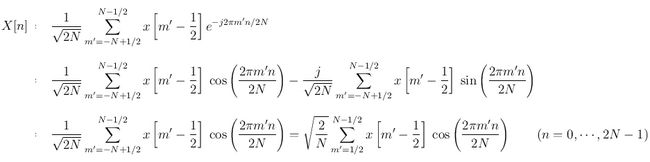
对上式的结果进行变换替换即可得DCT：

但是这时的DCT公式的变换矩阵不是正交矩阵，因为：

其实就是变换矩阵第一行不合适而已，进一下变形即可得到DCT公式：

详细的推导参见文献【5】，其它几种DCT参见文献【3】，这里就不再多说了。

三、离散正弦变换(Discrete SineTransform, DST)

类似于DCT，离散正弦变换也有八种形式，常用的是DST-Ⅰ，一般我们提到DST而不特殊说明即指DST-Ⅰ。

这里直接给出DST-Ⅰ的定义，与文献【2】和文献【6】均有一点儿不同：

上面两个式子中上面是DST正变换，下面是DST反变换。

因此可得到变换矩阵S_N

可以验证，变换矩阵S_N是一个正交矩阵，而且通过观察可以看出它还是一个对称矩阵（转置与本身相等），所以正变换与反变换是相同的。

四、如何得到DCT和DST变换基

（1）离散余弦变换基

在MATLAB中有dct函数可以进行dct变换：

这里形式上之所以和前面叙述的不太一样是因为matlab里的n和k都是从1到N的。

类似于离散傅里叶变换，要生成dct基（变换矩阵）的话有函数dctmtx可供使用，直接用dctmtx(N)即何生成N×N的DCT正交变换矩阵，打开dctmtx.m文件，核心代码只有三行：

[cc,rr] = meshgrid(0:n-1);
c = sqrt(2 / n) * cos(pi *(2*cc + 1) .* rr / (2 * n));
c(1,:) = c(1,:) / sqrt(2);

注意以上三行代码中的n即N×N矩阵的N。

（2）离散正弦变换基

Matlab中有dst函数用来计算离散正弦变换，但是类似于DFT，它的变换矩阵并不是一个完全的正交矩阵，需要外加一个定标因子才能变换正交矩阵，有关Matlab中的dst正变换和dst逆变换函数对应的公式分别如下：

从以上两个公式可以看出它类似于我们常见的DFT，DFT反变换中有个1/N定标因子，正变换中没有（此处是反变换中有个2/(N+1)）。

要生成dst基，matlab中没有现成的函数可供调用，不过比猫画虎，类似于dct基的三行生成代码可以得到dst基的生成代码：

[cc,rr] =meshgrid(0:N-1);
c = sqrt(2 / (N+1)) *sin(pi * (cc+1) .* (rr+1) / (N + 1));

五、结语

看dct和dst有几天了，总想看的更深入一些，感觉文献【2】的第八章还是不错的，但是讲的有些太简单了。正交变换是一个大家族，上一篇中说了正交变换有保范性质（变换前后参量不变），它还有一个大好处是变换矩阵是正交矩阵，其逆矩阵等于其转置，因此省去了求逆的麻烦。这些变换哪个好哪个坏呢？这就得说说KLT（Karhunen-Loève变换）了，KLT留着将常见的正交变换说完后再说吧。

 

参考文献：

【1】N.AHMED, T.NATARAJAN,K.R.RAO . Discrete Cosine Transform[J]. IEEE TRANSACTIONS ON COMPUTERS,1974,23(1)：90-93.

【2】胡广书.数字信号处理理论、算法与实现（第三版）[M]. 北京：清华大学出版社，2012：328-333.

【3】维基百科.离散余弦变换，

http://zh.wikipedia.org/wiki/%E7%A6%BB%E6%95%A3%E4%BD%99%E5%BC%A6%E5%8F%98%E6%8D%A2

【4】小火车. 离散余弦变换(DCT)的定义. 新浪博客：http://blog.sina.com.cn/s/blog_626631420100xvxd.html

【5】Definition ofDCT,http://fourier.eng.hmc.edu/e161/lectures/dct/node1.html

【6】维基百科.离散正弦变换，http://zh.wikipedia.org/wiki/离散正弦变换