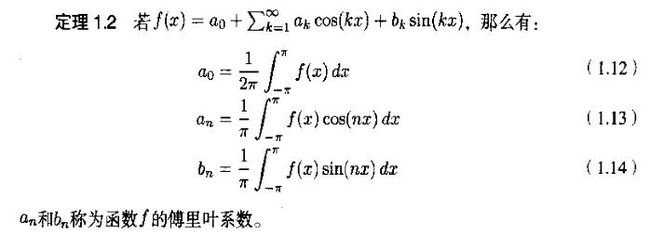傅里叶分析—傅里叶级数
名字起得很大。本文介绍Fourier级数、Fourier变换等基本数学概念及概念背后对应的物理意义。
一、傅里叶分析简介
展开成傅里叶级数的基本目的是要把一个信号(时间变量t的函数)分解为不同的频率分量。这些基本的构造块是正弦函数和余弦函数
sin(nt) cos(nt)
例如,考察下面的函数:f(t) = sin(t) + 2cos(3t) + 0.3sin(50t)
该函数有三个分量,其振荡频率为:1[sin(t)部分] 3[2cos(3t)部分] 50[0.3sin(50t)部分]。
信号分析中要解决的一个常见问题是:滤除噪声。例如,播放录音磁带时所特有的嘶嘶背景声就是一个高频(声音)噪声,有多种设备可以部分滤除它。0.3sin(50t)这部分造成了图1中f曲线的抖动,令系数0.3等于0,得到函数:f(t)=sin(t)+2cos(3t)
其图像除了没有高频抖动以外,与图1几乎一样。
这个例子显示了一个滤除噪声的方法,该方法就是把信号f(t)用正弦和余弦信号展开:
然后令与滤波频率相应的系数an、bn等于0。本例当中信号f已经表示成正弦和余弦的和的形式,所以处理过程很容易。然而,大多数信号不是以这种方式表示的。研究傅里叶级数的目的之一,就是要研究如何有效地把一个函数分解成正弦和余弦的分量之和,以便接着实现各种滤波算法。
二、傅立叶变换分类
根据原信号的不同类型,我们可以把傅立叶变换分为四种类别:
| 1 |
非周期性连续信号 |
傅立叶变换(Fourier Transform) |
| 2 |
周期性连续信号 |
傅立叶级数(Fourier Series) |
| 3 |
非周期离散信号 |
离散时域傅立叶变换(Discrete Time Fourier Transform) |
| 4 |
周期性离散信号 |
离散傅立叶变换(Discrete Fourier Transform) |
下图是四种原信号图例:
三、傅立叶级数的计算
该定理可以等价为集合
是L2([-π,π])上的正交函数系。
应用定理1.1就可以计算傅立叶级数的系数,得如下定理:
3.1.2 其他区间
3.2 余弦和正弦展开
下面是很有意思的一部分:偶延拓与奇延拓
=================================
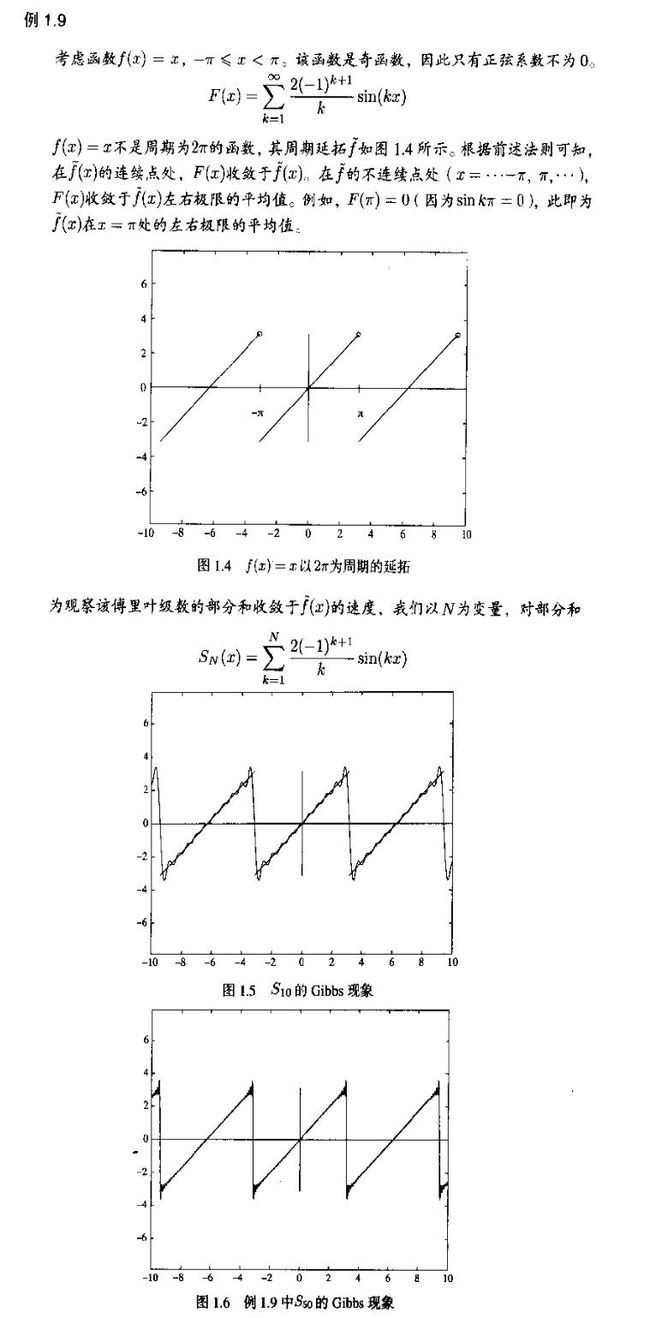
傅里叶级数的图像,可以看出可以很好得拟合原始函数
===================================
另一个例子:
3.3 傅里叶级数的复数形式
简要叙述:
3.4 傅里叶级数的收敛定理
简单罗列部分定理,在实际应用中,基本都满足收敛条件。
该定理说明:随着k增大,傅里叶系数ak和bk收敛于0。
连续点处的收敛定理:
不连续点处<但需要有左右极限存在>的收敛定理:
一致收敛性:
依平均收敛:
==========================================================
References:
1.小波与傅里叶分析基础
<这本书写得不错,很注重直观理解,但是缺少物理层面上的解释>
欢迎大家持续关注本博客,更多精彩内容请关注新浪微博:极度视界