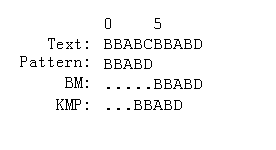Boyer-Moore文本匹配算法(联合使用KMP和Horspool算法)
Boyer-Moore除了考虑Horspool算法(参考笔者的另一篇专门介绍Horspool算法的文章)的坏字符之外,还将模式串中已经匹配成功的后缀(叫做好后缀,good suffix)考虑进来,从而得到全部已经知道的启发信息(heuristic)。因此从理论上来说,BM算法应该是性能最佳的一个算法,实践中也证明了这一点。 这也是为什么BM算法经常用作精确匹配算法里面的性能测试基准算法。例如,在通过下面的图示就可以看出, KMP算法由于没有考虑进来bad character信息,比较次数比BM算法稍多:
(图一)
上面在i=4,j=4时出现mismatch,在KMP算法中的做法是找出j-1右边界位置的失败函数值作为下一个j值,这里f(j-1)=1, 因此j'=1(i值不变,即下次仍然将P[j']跟T[i]=C比较)。这里KMP算法的第二步只移动了3个字符位置。而在BM算法中的做法是首先找出bad character(=C)的位移值,这里C在pattern中未出现,用BM算法的case 1(参考前面另一篇文章中的BM简化版-Horspool算法的介绍),将模式串沿着文本向右移动m个位置,即向右移5;然后找出good suffix(长度等于0)的位移值,由于good suffix长度等于0,位移值为1。最后取good suffix shift和bad character shift的最大位移值,等于5,所以得出上面BM算法中第二步的位置。
******************************************************
BM算法也是分两大步骤:1)预处理计算出bad character shift表(这一步跟Horspool算法中的做法一模一样,详细情况参考笔者的另一篇文章)和good suffix shift表;2)匹配。
匹配过程比较简单,即取bad character shift和good suffix shift值的最大值即可。从逻辑上来说,因为两个位移值都保证了不会遗漏能够成功匹配的子串,如果取最大值就可以更大幅度地将模式串向右移,从而减少比较次数。
设文本T长度为n,模式串P长度为m。T的当前位置指针为i(0<=i<n),P的当前位置指针为j(0<=j<m)。设good suffix的长度为k(0<=k<m,即模式串中长度为k的后缀已经跟文本相应字符匹配成功),即好后缀为P[m-k...m-1]。好后缀位移值是goodSuffixShiftTable[k]。
如果单考虑good suffix位移,可以分为以下几种情况(另外参考Horspool算法那篇文章介绍的bad character的cases):
case 1) k=0,即模式串中最后一个字符P[m-1]不匹配,做法是将模式串沿文本向右移动一个字符,即goodSuffixShiftTable[0]=1。
例如图二中case 1,这里X表示下一次模式串采用good suffix的位移位置。如果采用bad character位移,就是Y位置,从图中可见Y的移动幅度更大,在BM算法中应该取Y的位置。
case 2) k>0,但是在模式串中可以找到一个最右边的子串(非后缀)跟good suffix - P[m-k...m-1]完全相等。做法是将模式串沿文本向右移动goodSuffixShiftTable[k]个字符。例如在图二中case 2中,当j=2时,T[i]=C, P[j]=A,k=3,可以找到最右边的非后缀子串P[1...3]跟后缀BAB完全相等。这时需要将模式串沿文本向右移动2个字符,即goodSuffixShiftTable[3]=2。
(图二)
case 3) k>0,但是不能找到像case 2中的最右边的非后缀子串跟好后缀(good suffix)完全相等。可以分成两个小cases:
case 3a) 模式串中没有任何前缀(prefix)跟模式串的good suffix的一个后缀(而且是一个proper后缀)完全相等,做法是将模式串向右移动m个字符,即goodSuffixShiftTable[k]=m,例如图二中case 3a,这里j=1,T[i]=a,P[j]=z,k=2,显然没有任何prefix跟bc的唯一一个proper后缀“c”完全相等,于是得出X为模式串的下一次匹配位置。
case 3b) 模式串中存在一个最长的前缀(prefix)跟模式串的good suffix的一个后缀(而且是一个proper后缀)完全相等,做法是将模式串向右移动goodSuffixShiftTable[k]个字符。例如图二中case 3b,这里j=2,T[i]=z,P[j]=c,k=3,存在最长的前缀ab跟好后缀的后缀ab完全相等。goodSuffixShiftTable[3]=4。
在Horspool算法的基础上,坏字符位移值(bad character shift)可以根据下面的公式得出:
badCharShift = j+1-min(j,1+q)
好后缀位移值就是goodSuffixShiftTable[k]。
下一个i指针位置向右移动量为m - j + goodSuffixShiftTable[k] - 1,即下一个i += m - j + goodSuffixShiftTable[k] - 1; 下一个j值永远是模式串尾部,即m-1,这跟Horspool算法是一样的。
*******************************************************
下面介绍一下如何计算good suffix位移表:
这里利用KMP算法中计算失败函数的做法来计算BM算法中的good suffix位移表,复杂度为O(m)。这样做的原因是KMP算法中的failure function从本质上等价于BM算法中的good suffix shift table,因为二者都是根据已经匹配成功的字符序列计算出的结果,只是形成序列的扫描方向相反。
首先将模式串转成逆序R,然后对逆序模式串计算出它的KMP失败函数f(j)。对f(j)从右往左循环一遍,计算上面case 2(即最右边子串等于长度为k的后缀)中的good suffix shift值,循环结束时有这样的结果:
1)还有一部分k(k>=0)对应的good suffix shift值为0(即数组初始值),这时对应case 1,case 3a和case 3b(见下面的说明)。
2)f(j)>0,如果这样的f(j)有多个,循环最后的那个f(j)就相当于原始模式串最右边的子串长度(该子串等于原始模式串中长度为k=f(j)的后缀),所以这个f(j)就是k值。位移值采用如下公式计算:
(m - f[j]) - (m-j-1)
接下来设置goodSuffixShiftTable[0]=1,这是k=0(即case 1)时的一个特定值。
最后考虑某些k的good suffix shift仍然为0的情况。因为f(m-1)就是case 3中匹配到的最长前缀。见下图中蓝色部分区域。如果f(m-1)=0,就是case 3a,位移值设置为m。
如果f(m-1)>0,对应case 3b,这时goodSuffixShiftTable[k]应修正为m-f(m-1),即将模式串首字符跟长度为f(m-1)的后缀的首字符对齐。需要说明的是,在这种情况下(即f(m-1)>0), 这样的k必定满足条件k>f(m-1),用反证法证明:到目前为止goodSuffixShiftTable[k]=0的那些k值如果满足0<k<=f(m-1)的话,在上面2)中得到的结果会有goodSuffixShiftTable[k]>0, 理由是k<=f(m-1)说明一定存在一个长度为k子串与某一个长度为k的后缀完全相等,即满足case 2,显然对于case 2的情况必有goodSuffixShiftTable[k]>0,与goodSuffixShiftTable[k]=0前提矛盾。这也是为什么下面实现代码中用"if(goodSuffixShift[k]==0)"代替"if(goodSuffixShift[k]==0 && prefixMaxLen<k)"的原因。
下图中的S就是good suffix shift值列表。
(图三)
实现:
import java.util.Arrays;/** * * Boyer-Moore Algorithm * * Copyright (c) 2011 ljs (http://blog.csdn.net/ljsspace/) * Licensed under GPL (http://www.opensource.org/licenses/gpl-license.php) * * @author ljs * 2011-06-21 * */public class BM {private static final int CHARSET_SIZE = 256;//prepare the shift table: find the rightmost position //in the patternprivate int[] makeBadCharTable(String pattern){int[] shiftTable = new int[CHARSET_SIZE];//init to -1for(int i=0;i<CHARSET_SIZE;i++)shiftTable[i]=-1;//set the pattern charsfor(int i=0;i<pattern.length();i++){char c = pattern.charAt(i);//OK: the rightmost position i may overwrite the left positionsshiftTable[c] = i;}return shiftTable;}//caculate KMP algorithm's failure function: f[0], f[1..m-1], m is the length of patternprivate int[] calFailureF(String pattern){int m = pattern.length();int[] f = new int[m];//i is the right border positionint i = 1;int j = 0;f[0] = 0; //by definitionwhile(i<m){if(pattern.charAt(i)==pattern.charAt(j)){//j is index from 0, f[i] is the length of suffix/prefix//so we need to add 1f[i] = j + 1; i++;j++;}else if(j==0){//find no valid prefix f[i] = 0; //move i only, j is still 0i++;}else{//move j only, i doesn't change position, thus f[i]'s value is not determined yet.//reuse the KMP algorithm: we already know f[j-1]'s value j = f[j-1];}}return f;}//using KMP algorithm's failure function to caculate good-suffix shift tableprivate int[] makeGoodSuffixShiftTable(String pattern){ String reverse = new StringBuffer(pattern).reverse().toString(); int[] f = calFailureF(reverse); int m = pattern.length(); int[] goodSuffixShift = new int[m]; //set goodSuffixShift by failure function for(int j=m-1;j>=0;j--){ //caculate d2 int index = m - j - 1; //the original(not reversed) index // e.g....BCD...BCD, the first BCD's start index = m - j - 1 // the length of BCD is f[j]; m - f[j] is the last BCD's start index // so m-f[j]-index is the shift distance from first B to the second B // if f[j] = 0, the goodSuffixShift[0] is always set with value 1 after // this loop int d2 = m - f[j] - index; //case 2 (f[j]>0) goodSuffixShift[f[j]] = d2; if(f[j]>0) { //only the last displayed k (rightmost) is valid System.out.format("k=%d: %d - > %d%n",f[j],index,m - f[j]); } } //case 1 goodSuffixShift[0] = 1; //j = 0; //case 3a and 3b (i.e. no substring fully overlapped suffix-k) int prefixMaxLen = f[m-1]; for(int k=1;k<=m-1;k++){ // goodSuffixShift[k]==0 is default value for int array //ie. no substring fully overlapped suffix-k //if(goodSuffixShift[k]==0 && prefixMaxLen<k){ if(goodSuffixShift[k]==0){ //if prefixMaxLen = 0, we hit case 3a; otherwise case 3b goodSuffixShift[k] = m - prefixMaxLen; System.out.format("k=%d: %d - > %d%n",k,0,m - prefixMaxLen); } } BM.printGoodSuffixShift(pattern,reverse,f,goodSuffixShift); return goodSuffixShift;}//return the first matched substring's position;//return -1 if no matchpublic int match(String text,String pattern){int n = text.length();int m = pattern.length();if(m>n) return -1;int[] badCharTable = makeBadCharTable(pattern);int[] goodSuffixShiftTable = makeGoodSuffixShiftTable(pattern);/****BEGIN TEST: the following code snippet can be commented out****/StringBuilder sb = new StringBuilder();for(int i=0;i<text.length();i++){if(i%5==0){sb.insert(i, String.valueOf(i));}else{sb.append(" ");}}System.out.format("%s%n",sb.toString());System.out.format("%s%n",text);System.out.format("%s%n",pattern);/****END TEST: the above code snippet can be commented out****/int i = m -1;int j = m -1;do{int c = text.charAt(i);if(c == pattern.charAt(j)){if(j==0){//find a matchreturn i;}else{//BM algorithm: move from right to lefti--;j--;}}else{//use bad character shiftint i_temp_badChar = i;//determine the i and j for next match attemptint p = badCharTable[c] + 1;int badCharShift = 1;if(j<=p){i_temp_badChar += m - j;}else{i_temp_badChar += m - p;badCharShift += j - p;}//or caculate the shift for bad character this way://Note the fact: i_temp_badChar>i, j>j_last/* int badCharShift = (i_temp_badChar - i) - ((m-1) - j);if(badCharShift < 0)badCharShift = -badCharShift;*/ //use good suffix shift//the length of good suffixint i_temp_goodSuffix = i;int k = m - j - 1;int goodSuffShift = goodSuffixShiftTable[k];i_temp_goodSuffix += m - j + goodSuffShift - 1;//use the max shift between good-suffix and bad-characterif(goodSuffShift > badCharShift)i = i_temp_goodSuffix;else i = i_temp_badChar;//BM algorithm: move j to the end of patternj = m - 1;/****BEGIN TEST: the following code snippet can be commented out****/int dotsCount = i - j;byte dot[] = new byte[dotsCount]; Arrays.fill(dot, (byte)'.');System.out.format("%s%s%n",new String(dot),pattern);/****END TEST: the above code snippet can be commented out****/}}while(i<=n-1);return -1;}//for test purpose onlypublic static void printGoodSuffixShift(String pattern,String revPattern,int[] failureFunc,int[] goodSuffixShift){//pattern index positionsSystem.out.print("i:");for(int i=0;i<pattern.length();i++){System.out.format(" %2s", i);}System.out.println();//the original patternSystem.out.print("P:");for(int i=0;i<pattern.length();i++){System.out.format(" %2s", pattern.charAt(i));}System.out.println();//reversed pattern System.out.print("R:");for(int i=0;i<revPattern.length();i++){System.out.format(" %2s", revPattern.charAt(i));}System.out.println();//failure function output for reversed patternSystem.out.print("f:");for(int i=0;i<failureFunc.length;i++){System.out.format(" %2d", failureFunc[i]);}System.out.println();//good suffix shiftSystem.out.println();System.out.print("S:");for(int k=0;k<goodSuffixShift.length;k++){System.out.format(" %2d", goodSuffixShift[k]);}System.out.println();System.out.println();}//for test purpose onlypublic static void findMatch(BM solver,String text,String pattern){int index = solver.match(text, pattern);if(index>=0){System.out.format("Found at position %d%n",index);}else{System.out.format("No match%n");}}public static void main(String[] args) {BM bm = new BM();String pattern = "ABCBAB";bm.makeGoodSuffixShiftTable(pattern);System.out.println("**********************");pattern = "zzbc";bm.makeGoodSuffixShiftTable(pattern);System.out.println("**********************");pattern = "CBABAB";bm.makeGoodSuffixShiftTable(pattern);System.out.println("**********************");pattern = "ABABAB";bm.makeGoodSuffixShiftTable(pattern);System.out.println("**********************");String text = "A SLOW TURTLE";pattern = "NEEDLE";BM.findMatch(bm,text,pattern);System.out.println("**********************");text = "After a long text, here's a needle ZZZZZ";pattern = "ZZZZZ";BM.findMatch(bm,text,pattern);System.out.println("**********************");text = "The quick brown fox jumps over the lazy dog.";pattern = "lazy";BM.findMatch(bm,text,pattern);System.out.println("**********************");text = "Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna...";pattern = "tempor";BM.findMatch(bm,text,pattern);System.out.println("**********************");text = "GGGGGGGGGGGGCGCAAAAGCGAGCAGAGAGAAAAAAAAAAAAAAAAAAAAAA";pattern = "GCAGAGAG";bm.makeGoodSuffixShiftTable(pattern);BM.findMatch(bm,text, pattern);}}
测试输出:
k=2: 0 - > 4k=1: 1 - > 5k=1: 3 - > 5k=3: 0 - > 4k=4: 0 - > 4k=5: 0 - > 4i: 0 1 2 3 4 5P: A B C B A BR: B A B C B Af: 0 0 1 0 1 2S: 1 2 4 4 4 4**********************k=1: 0 - > 4k=2: 0 - > 4k=3: 0 - > 4i: 0 1 2 3P: z z b cR: c b z zf: 0 0 0 0S: 1 4 4 4**********************k=3: 1 - > 3k=2: 2 - > 4k=1: 3 - > 5k=4: 0 - > 6k=5: 0 - > 6i: 0 1 2 3 4 5P: C B A B A BR: B A B A B Cf: 0 0 1 2 3 0S: 1 2 2 2 6 6**********************k=4: 0 - > 2k=3: 1 - > 3k=2: 2 - > 4k=1: 3 - > 5k=5: 0 - > 2i: 0 1 2 3 4 5P: A B A B A BR: B A B A B Af: 0 0 1 2 3 4S: 1 2 2 2 2 2**********************k=1: 1 - > 5k=1: 2 - > 5k=2: 0 - > 6k=3: 0 - > 6k=4: 0 - > 6k=5: 0 - > 6i: 0 1 2 3 4 5P: N E E D L ER: E L D E E Nf: 0 0 0 1 1 0S: 1 3 6 6 6 60 5 10 A SLOW TURTLENEEDLE......NEEDLE.......NEEDLE.............NEEDLENo match**********************k=4: 0 - > 1k=3: 1 - > 2k=2: 2 - > 3k=1: 3 - > 4i: 0 1 2 3 4P: Z Z Z Z ZR: Z Z Z Z Zf: 0 1 2 3 4S: 1 1 1 1 10 5 10 15 20 25 30 35 After a long text, here's a needle ZZZZZZZZZZ.....ZZZZZ..........ZZZZZ...............ZZZZZ....................ZZZZZ.........................ZZZZZ..............................ZZZZZ...................................ZZZZZFound at position 35**********************k=1: 0 - > 4k=2: 0 - > 4k=3: 0 - > 4i: 0 1 2 3P: l a z yR: y z a lf: 0 0 0 0S: 1 4 4 40 5 10 15 20 25 30 35 40 The quick brown fox jumps over the lazy dog.lazy....lazy........lazy............lazy................lazy....................lazy........................lazy............................lazy................................lazy...................................lazyFound at position 35**********************k=1: 0 - > 6k=2: 0 - > 6k=3: 0 - > 6k=4: 0 - > 6k=5: 0 - > 6i: 0 1 2 3 4 5P: t e m p o rR: r o p m e tf: 0 0 0 0 0 0S: 1 6 6 6 6 60 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100 105 110 115 Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna...tempor......tempor............tempor..................tempor.....................tempor...........................tempor...............................tempor....................................tempor..........................................tempor................................................tempor......................................................tempor..........................................................tempor...........................................................tempor.................................................................tempor..................................................................tempor........................................................................tempor.........................................................................temporFound at position 73**********************k=1: 0 - > 7k=4: 2 - > 4k=3: 3 - > 5k=2: 4 - > 6k=1: 5 - > 7k=5: 0 - > 7k=6: 0 - > 7k=7: 0 - > 7i: 0 1 2 3 4 5 6 7P: G C A G A G A GR: G A G A G A C Gf: 0 0 1 2 3 4 0 1S: 1 2 2 2 2 7 7 7k=1: 0 - > 7k=4: 2 - > 4k=3: 3 - > 5k=2: 4 - > 6k=1: 5 - > 7k=5: 0 - > 7k=6: 0 - > 7k=7: 0 - > 7i: 0 1 2 3 4 5 6 7P: G C A G A G A GR: G A G A G A C Gf: 0 0 1 2 3 4 0 1S: 1 2 2 2 2 7 7 70 5 10 15 20 25 30 35 40 45 50 GGGGGGGGGGGGCGCAAAAGCGAGCAGAGAGAAAAAAAAAAAAAAAAAAAAAAGCAGAGAG..GCAGAGAG....GCAGAGAG......GCAGAGAG...........GCAGAGAG............GCAGAGAG..............GCAGAGAG...................GCAGAGAG.......................GCAGAGAGFound at position 23