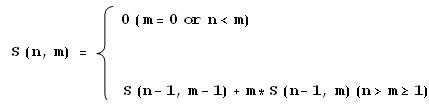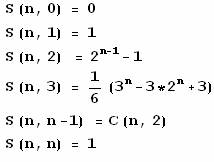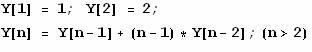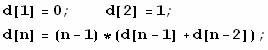数论-Special Numbers

1. Fibonacci Number

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377, 610 …

Formula:

2.           Lucas Number

1, 3, 4, 7, 11, 18, 29, 47, 76, 123...

Formula:

3.           Catalan Number

1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786,208012…

Formula:

Application:

1)      将 n + 2 边形沿弦切割成 n个三角形的不同切割数

2)      n + 1个数相乘, 给每两个元素加上括号的不同方法数

3)      n 个节点的不同形状的二叉树数(严《数据结构》P.155)

4)      从n * n 方格的左上角移动到右下角不升路径数

 

4.           StirlingNumber(Second Kind)

S(n, m)表示含n个元素的集合划分为m个集合的情况数

或者是n个有标号的球放到m 个无标号的盒子中, 要求无一为空, 其不同的方案数

Formula:

Special Cases:

      

5.           BellNumber

n 个元素集合所有的划分数

Formula:

     

 

6.           Stirling's Approximation

7.           Sum of Reciprocal Approximation

EulerGamma = 0.57721566490153286060651209;

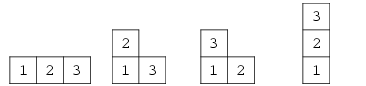
8.           Young Tableau

Young Tableau(杨式图表)是一个矩阵, 它满足条件:

如果格子[i, j]没有元素, 则[i+1, j]也一定没有元素

如果格子[i, j]有元素a[i, j],则[i+1, j]要么没有元素, 要么a[i+1, j] > a[i, j]

Y[n]代表n个数所组成的杨式图表的个数

Formula:

    

Sample:

n = 3;   

 

9.           整数划分

将整数n分成k份, 且每份不能为空, 任意两种分法不能相同

1) 不考虑顺序

for(int p=1; p<=n ;p++)
     for(int i=p; i<=n ;i++)
          for(int j=k; j>=1 ;j--)
               dp[i][j] += dp[i-p][j-1];
cout<< dp[n][k] <<endl;

2) 考虑顺序

dp[i][j] = dp[i-k][j-1]; (k=1..i)

3) 若分解出来的每个数均有一个上限m

dp[i][j] = dp[i-k][ j-1];(k=1..m)

10.      错排公式