HDU 4582 DFS spanning tree 解题报告(贪心 & 树形DP)
此题贪心可解。从下往上,到了必须选边的时候才选边即可。296MS,代码如下:
#include <bitset>
#include <iostream>
using namespace std;
const int maxn=2013;
int first[maxn],pre[maxn],vv[maxn*20],nxt[maxn*20];
bitset<2001> to[2001];
bool vis[maxn];
int ans;
void dfs(int u,int p)
{
vis[u]=true;
to[u].reset();
for(int e=pre[u];e;e=nxt[e]) if(vis[vv[e]])
to[u].set(vv[e]);
for(int e=first[u];e;e=nxt[e]) if(vv[e]!=p)
dfs(vv[e],u);
if(p==-1)
return;
if(to[u].test(p))
ans++;
else
to[p]|=to[u];
}
int main()
{
int n,m;
while(~scanf("%d%d",&n,&m) && n|m)
{
memset(vis,0,sizeof(vis));
memset(first,0,sizeof(first));
memset(pre,0,sizeof(pre));
int e=2;
for(int i=1;i<n;i++)
{
int u,v;
scanf("%d%d",&u,&v);
nxt[e]=first[u],vv[e]=v,first[u]=e++;
nxt[e]=first[v],vv[e]=u,first[v]=e++;
}
for(int i=n;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
nxt[e]=pre[u],vv[e]=v,pre[u]=e++;
nxt[e]=pre[v],vv[e]=u,pre[v]=e++;
}
ans=0;
dfs(1,-1);
printf("%d\n",ans);
}
}
当然,之前写的树形DP也是可以过的。
首先声明,参考了frog1902的解题报告。http://blog.csdn.net/frog1902/article/details/9921845
这里是另外一份解题报告的地址:http://www.cnblogs.com/wangfang20/archive/2013/08/13/3254920.html
其实我都看了,仍然不是太懂。在画了很多图,debug许久后,终于有点理解了。希望和我一样不懂的弱菜能看懂= =。
首先是题意:给定n个点,m条边的图。前n-1条边是DFS树。所说的T环是只有一条边不属于DFS树的环。问最小选取多少条边,可以使所有的T环都能被覆盖到。
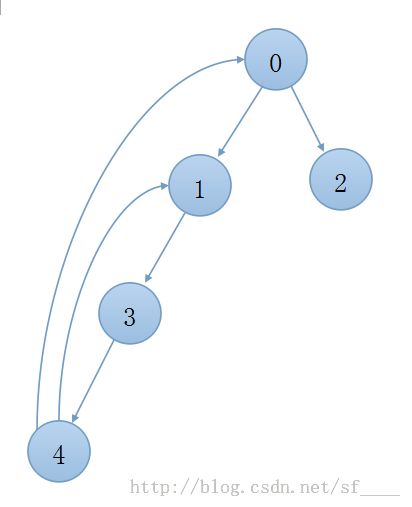
图中 1,2,3,1 是一个T环,1,2,4,1是一个T环。只要选择(1,2)这条边,那么两个T换都被覆盖到了。
frog1902的解题报告中所说的横叉边与返祖边,简单引用并解释下:
=====================================================
“需注意的是,题目给出的是一个无向图的DFS树,
所以不在这棵树上的边一定不可能是"横叉边",而一定是" 后向边(返祖边)"。
也就是说,不在DFS树上的边,一定是由某点指向它的某个祖先的。
很容易想象,如果不是这样,那么DFS树的形态一定会发生改变。”
=====================================================
横叉边是某一节点x到DFS树中另一子树上节点y的边,返祖边是某一节点x到其DFS树中祖先y的边。如下图:
算法导论中DFS那里有说明,不懂大家可以去看一下。
题中所说的a Depth-First-Search(DFS) spanning tree T of a undirected connected graph G。图是无向图,所以不会有类似于7->5这样的横叉边,以为无向,所以如果5,7间有边,遍历到5时,7就是5的子节点了。对于无向边(u,v),假设DFS到u点。如果u点通过其他路径访问了v点,DFS v点时发现u被标记过,自然不会走(u,v),(u,v)边自然就是不属于DFS树,相当于反向边。否则u一定会通过(u,v)边访问v,自然不存在横叉边。
理解完这些后,就可以思考下怎么做了。
上图中存在(4,1),(4,0)构成的两个T环。显然当小环中选边时大环自然也选边了。我们可以用lim[u]记录与u节点的最小环中选边的最小深度。我们用dep[u]记录u点的深度,一遍DFS既可以求出所有点的深度了。图中1,3,4,1构成的T环中,我们可以选择(1,3)边或者(3,4)边。则lim[u]的值为节点3的深度,2。也就是说这里定义一条边的深度以为深度较大节点的深度,选择3节点即为选择3节点和3节点的父节点构成的边。
那么对于u节点来说,选边时应该选择深度为[ lim[u],dep[u] ] 的边。
接下来是dp[u][k]的定义。定义dp[u][k]为对于节点u,在选择了深度为k的边后,以u点为根节点的树中还需要选择多少条边。
首先看dp[0][0]。dp[0][0]就是对于节点0,选择了深度为0的边后,以0为根节点的树中还需要多少边。我们假象0节点上有一个-1节点,这样比较好理解。而dp[0][0]看起来就是我们最终要求的值。如下图:
同样,lim[u]=0就代表u节点可以选择(-1,0)这条边,当然这条边不在计数内。
如何求dp[u][k]的值呢?对于任一子节点v来说,dp[v][j]的合理取值是lim[v]<=j<=dep[v]。对于dp[u][k]来说,合理取值是lim[u]<=k<=dep[u]。我们希望dp[u][k]尽量小,那么选择了深度为k的边后,dp[v][j]如果存在j,满足lim[v]<=j<=k,那么在这一区间内的最小的dp[v][j]是满足条件的。因为选择了k边,j满足lim[v]<=j<=k,说明v点形成的T环里有了符合条件的深度为k的边被选择了。当然,对于区间lim[u]<=k<=dep[u]内所有的边,我们可以选择k边,再选择(v,u)这条边。我们在所有的可能中选择最小值。所以我们将(v,u)这条边计算在dp[u][dep[u]]中。
举个例子:当u为节点3时。节点3中,dp[3][k],深度k可以是0,1,2。也就是(-1,0),(0,1),(1,3)这3条边。当我们选(-1,0)时,显然节点4的lim[4]深度大了点,我们需要同时选择(3,4)这条边。当我们选择(1,3)这条边时,节点4的需求也满足了,也就不要选择(3,4)这条边了。对于所有的dp[u][k],我们都让它们取最小值,这样最终的dp[0][0]是最小的。
在下表达能力欠佳,如果不懂,可以直接回复= =。
代码中相当于选择了(-1,0)这条边,所以最后的答案减1了。杭电上时984MS,代码如下:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxV=2013;
int first[maxV],vv[maxV<<1],nxt[maxV<<1];
int dp[maxV][maxV];
int lim[maxV],dep[maxV];
void DFS(int u,int p)
{
for(int e=first[u];e;e=nxt[e]) if(vv[e]!=p)
{
dep[vv[e]]=dep[u]+1;
DFS(vv[e],u);
}
}
void DP(int u,int p)
{
for(int i=lim[u];i<=dep[u];i++)
dp[u][i]=0;
for(int e=first[u];e;e=nxt[e]) if(vv[e]!=p)
{
int v=vv[e];
DP(v,u);
int temp=dp[v][dep[v]];
for(int i=lim[v];i<lim[u];i++)
temp=min(temp,dp[v][i]);
for(int i=lim[u];i<=dep[u];i++)
{
temp=min(temp,dp[v][i]);
dp[u][i]+=temp;
}
}
dp[u][dep[u]]++;
}
int main()
{
int n,m;
while(~scanf("%d%d",&n,&m) && n|m)
{
memset(lim,0,sizeof(lim));
memset(dp,0x7f,sizeof(dp));
memset(first,0,sizeof(first));
int e=2;
for(int i=1;i<n;i++)
{
int u,v;
scanf("%d%d",&u,&v);
u--,v--;
nxt[e]=first[u],vv[e]=v,first[u]=e++;
nxt[e]=first[v],vv[e]=u,first[v]=e++;
}
dep[0]=0;
DFS(0,-1);
for(int i=n;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
u--,v--;
if(dep[u]<dep[v])
swap(u,v);
lim[u]=max(lim[u],dep[v]+1);
}
DP(0,-1);
printf("%d\n",dp[0][0]-1);
}
}