学习SIFT算法过程中的释疑
介绍SIFT算法的文章
David G. Lowe, "Distinctive image features from scale-invariant keypoints,"International Journal of Computer Vision, 60, 2 (2004), pp. 91-110
文章一开始就给出了sift特征的关键步骤:
1. 利用尺度空间,检测极值点
2. 对极值点(关键点)精确定位,以及剔除一些不好的特征点
3. 对关键点生成方向参数
4. 生成关键点的特征描述符
一开始接触SIFT算法,在这些步骤中,还有很多不理解的地方,看了原文和一些blog,才有点感觉,这里总结下这个过程中的疑问和答案。
2. 为什么是DOG算子,Gaussian算子,为什么不是LOG算子?
3. 为什么原图像有时长宽扩大一倍?为什么需要高斯金字塔的降采样,形成octave的形式?
4. 多尺度是指哪些?
5. 什么是octave?
6. 空间尺度的连续性怎么理解?
7. 对旋转不变性、亮度变化不变性体现在什么地方?
参考的一些blog,写的真不错:
http://blog.csdn.net/sunminmin2011/article/details/8130090
http://wenku.baidu.com/view/dc5fffec102de2bd9605886e.html
http://www.360doc.com/content/11/1230/23/3054335_176200661.shtml
http://blog.csdn.net/abcjennifer/article/details/7639681
有关特征的一些概念:
图像的变化形式: 旋转、尺度变换、仿射变换、视角变换、光照变化等。
不变量: 同一场景下,图像有些变化,但图像中仍有保持稳定不变的特征,对这些特征的描述,就称为不变量
尺度不变量: 图像尺度有变化时,那些不变的特征就称为尺度不变量
旋转不变量: 图像旋转时,那些不变的特征就称为旋转不变量
常用的图像特征: 角点(局部极值点)、边缘、轮廓
稳定的特征向量: 将多种特征组合、变换,形成稳定的特征向量,即不受图像尺度、旋转等变换的影响。
多尺度下的极值点:一般来说,测试一点是否是极值点,就是比较此点与周围的点,当此点比周围的点都大时,其就是极值点;但多尺度下的极值点,不仅要求此点在原图上是极值点,还要求其比其他尺度空间的同范围的点值都大。这个性质就是尺度不变量,这个是定义。
特征描述子(符):拿到特征点后,利用特征点及其邻域的信息,如梯度等,转化为一个数值向量,最好与特征点的位置,scale等空间特征无关。这个数值向量形成了特征空间。无论特征点的空间位置及其他环境如何变化,特征空间对其的描述表示,保持稳定。
-------------------
1. 基础知识:尺度空间理解
一般的尺度变换理解:
尺度,首先从信号处理来理解这个概念,对信号的尺度变换,就对信号进行缩放,比如对时域扩展,频域就收缩 !!!-_-, 要复习信号的一些知识。
对图像的尺度变换的形式: 一种就是将图像直接缩放成不同的大小。常见金字塔抽样,就是这种尺度变换的一种。
其他尺度变换的形式:
高斯尺度变换
小波变换
以及更泛化的 多分辨率尺度变换
http://blog.csdn.net/tanxinwhu/article/details/7048370 尺度空间理解介绍
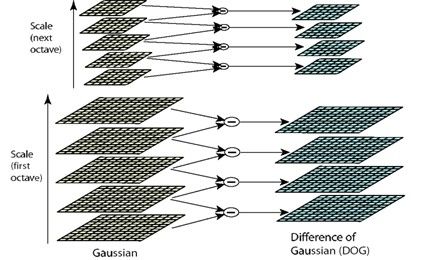
2. 为什么是DOG算子,Gaussian算子,为什么不是LOG算子?
DOG/LOG算子就是借助高斯尺度变换的特征。确切的说应该是LOG特征,Mikolajczyk发现LOG的极值点(极大值和极小值)比梯度(一阶导数),Hessian(二阶导数矩阵),及harris角点具有更稳定的特征。而DOG具有近似LOG的性质,且比LOG的运算效率更高。
Gaussian滤波器,压制高频信息,而DOG算子在Gaussian滤波器压制高频的基础上,又压制了低频的区域,形成一个带通滤波器。带通,指指定频带通过,在空域上,表现为指定尺度的细节图像保留下来。这个要比普通的高频锐化算法 检测细节的效果好,因为高频锐化不仅增强了细节,还增强了高频噪声。图像增强时,DOG算法中两个高斯核的半径之比通常为4:1或5:1。
DOG算子如何简化计算?
而与LOG算子比较,DOG算子其尺度变化更自由,当高斯核半径比为1:1.6时,才是LOG算子的近似。
DOG算子具有LOG归一化的近似的性质,计算更方便、速度更快,所以采用DOG算子。
3. 为什么原图像有时长宽扩大一倍?
有时采用双线性插值扩大一倍,目的同高斯金字塔降采样一样,是为了scale上扩大采集特征点的范围,以实用多尺度scale的匹配
有了高斯尺度空间,大的标准差对应图像概貌,提取云朵之类的低频特征比较丰富的特征点,小的标准差对应图像细节,提取高频细节比较丰富的特征点,为什么还需要高斯金字塔的降采样,形成octave的形式?
应该是为了达到图像匹配时,有尺度缩放不变性的能力。形成了关键点的坐标(scale, x, y)三维空间的形式。尺度不变性,其实就是具有提取多尺度的特征,以适应各种尺度的场景。
4. 多尺度是指哪些?
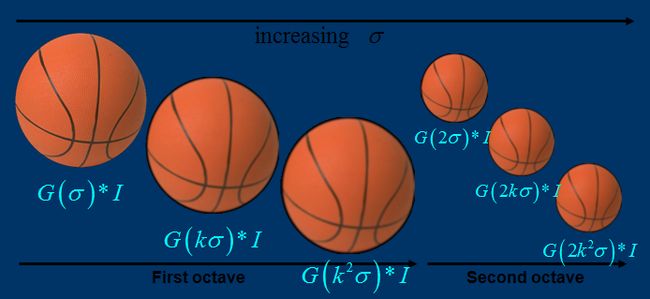
1. 高斯系数的变化: 在图像大小不变的情况下,改变高斯函数标准差的大小,其比例系数1, k, k^2,... , k^n
2. 空间分辨率的变化: 金字塔式抽样,改变图像大小,对图像进行间隔抽样,或者双线性插值抽样。
如下图:
5. 什么是octave?
octave不一定就是高斯系数变化从1到 K^7,得到八个图像,一般不需要这么多,3-5个处理层次就可以了。每一级空间抽样(空间分辨率变化)都会有自己独立的octave高斯尺度处理。这样原文里的scale图示就比较好理解了。
6. 空间尺度的连续性怎么理解?
每相邻两个octave之间的序列 高斯函数有一定联系。
如octave1,其序列高斯函数为 1, k, k^2,... , k^n, octave2 高斯序列函数为 2*1,2 * k, 2 * k^2,... ,2 * k^n.
由于取k = 2^(1/s), octave1中第s层的高斯函数,就等于octave2中的第一层的高斯函数。从这个层面上,高斯空间尺度就连起来了。
其好处是什么? 应该是针对特征点的选取,尺度空间连续,那么如特征点的选取,在不同尺度就不会有遗漏。若值选取一个最大尺度,和一个最小尺度, 那么就只会选取出最大尺度的特征点,以及最细节的特征点,而中间尺度的细节特征点就没选取到,这就是尺度空间不连续造成的。个人理解。
而空间分辨率上,降采样还是要做的,即octave1与octave2即使部分序列的高斯函数一样,但其图像的大小还是不同的。
7. 对旋转不变性体现在什么地方?
特征点是依赖于位置信息的,所以也隐含着角度旋转的信息。要除去旋转角度信息的依赖性,就是设计一种旋转不变的特征描述子。
一般特征点附近的 梯度 方向,加上特征点的位置,尺度,都是特征点的信息。将这些信息转换为方向无关的信息。
计算特征点的方向,然后将坐标轴旋转为特征点的方向,这样就保证了以后的计算与方向无关了。
计算出这个特征点的16*16邻域的所有点的梯度和方向。再划分为4*4的小窗口,计算每个小窗口的8个主方向(将每个方向上的梯度值累加),形成4*4*8=128的描述子。文章里介绍的更清楚。
对亮度变化不变性体现在什么地方?
对上述描述子,进行归一化,这样就降低了亮度变化的不变性。
什么样的点是不好的特征点?为什么?
去除低对比度的关键点和不稳定的边缘响应点。
对于特征对比度,给定一个阈值,只有大于这个阈值才保留。
而对于边缘响应,通过hessien矩阵来计算其主曲率。将主曲率大的响应点去除。对于边缘响应点,其曲率也是比较大的。